Πώς να βρείτε τη διαβάθμιση μιας συνάρτησης σε ένα σημείο παραδείγματα. Κλίση συνάρτησης. Ακραία συνάρτησης πολλών μεταβλητών

Είναι γνωστό από ένα σχολικό μάθημα μαθηματικών ότι ένα διάνυσμα σε ένα επίπεδο είναι ένα κατευθυνόμενο τμήμα. Η αρχή και το τέλος του έχουν δύο συντεταγμένες. Οι διανυσματικές συντεταγμένες υπολογίζονται αφαιρώντας τις συντεταγμένες έναρξης από τις συντεταγμένες τέλους.

Η έννοια του διανύσματος μπορεί επίσης να επεκταθεί σε έναν ν-διάστατο χώρο (αντί για δύο συντεταγμένες θα υπάρχουν n συντεταγμένες).

Βαθμίδα grad z της συνάρτησης z = f(х 1 , х 2 , …х n) είναι το διάνυσμα μερικών παραγώγων της συνάρτησης στο σημείο, δηλ. διάνυσμα με συντεταγμένες.

Μπορεί να αποδειχθεί ότι η κλίση μιας συνάρτησης χαρακτηρίζει την κατεύθυνση της ταχύτερης αύξησης του επιπέδου της συνάρτησης σε ένα σημείο.

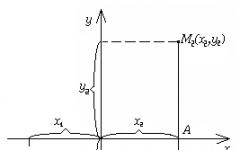
Για παράδειγμα, για τη συνάρτηση z \u003d 2x 1 + x 2 (βλ. Εικόνα 5.8), η κλίση σε οποιοδήποτε σημείο θα έχει συντεταγμένες (2; 1). Μπορεί να κατασκευαστεί σε ένα επίπεδο με διάφορους τρόπους, λαμβάνοντας οποιοδήποτε σημείο ως αρχή του διανύσματος. Για παράδειγμα, μπορείτε να συνδέσετε το σημείο (0; 0) στο σημείο (2; 1) ή το σημείο (1; 0) στο σημείο (3; 1) ή το σημείο (0; 3) στο σημείο (2; 4), ή τ .Π. (βλ. εικόνα 5.8). Όλα τα διανύσματα που κατασκευάζονται με αυτόν τον τρόπο θα έχουν συντεταγμένες (2 - 0; 1 - 0) =
= (3 – 1; 1 – 0) = (2 – 0; 4 – 3) = (2; 1).

Το σχήμα 5.8 δείχνει ξεκάθαρα ότι το επίπεδο της συνάρτησης αυξάνεται προς την κατεύθυνση της κλίσης, αφού οι κατασκευασμένες γραμμές επιπέδου αντιστοιχούν στις τιμές επιπέδου 4 > 3 > 2.

Εικόνα 5.8 - Συνάρτηση κλίσης z \u003d 2x 1 + x 2

Εξετάστε ένα άλλο παράδειγμα - τη συνάρτηση z = 1/(x 1 x 2). Η κλίση αυτής της συνάρτησης δεν θα είναι πλέον η ίδια σε διαφορετικά σημεία, αφού οι συντεταγμένες της καθορίζονται από τους τύπους (-1 / (x 1 2 x 2); -1 / (x 1 x 2 2)).

Το σχήμα 5.9 δείχνει τις γραμμές επιπέδου της συνάρτησης z = 1 / (x 1 x 2) για τα επίπεδα 2 και 10 (η ευθεία γραμμή 1 / (x 1 x 2) = 2 υποδεικνύεται με μια διακεκομμένη γραμμή και η ευθεία γραμμή
1 / (x 1 x 2) \u003d 10 - συμπαγής γραμμή).

Εικόνα 5.9 - Διαβαθμίσεις της συνάρτησης z \u003d 1 / (x 1 x 2) σε διάφορα σημεία

Πάρτε, για παράδειγμα, το σημείο (0,5; 1) και υπολογίστε τη διαβάθμιση σε αυτό το σημείο: (-1 / (0,5 2 * 1); -1 / (0,5 * 1 2)) \u003d (-4; - 2) . Σημειώστε ότι το σημείο (0,5; 1) βρίσκεται στη γραμμή επιπέδου 1 / (x 1 x 2) \u003d 2, επειδή z \u003d f (0,5; 1) \u003d 1 / (0,5 * 1) \u003d 2. Προς απεικονίσετε το διάνυσμα (-4; -2) στο σχήμα 5.9, συνδέουμε το σημείο (0.5; 1) με το σημείο (-3.5; -1), επειδή
(-3,5 – 0,5; -1 - 1) = (-4; -2).

Ας πάρουμε ένα άλλο σημείο στην ίδια γραμμή επιπέδου, για παράδειγμα, σημείο (1; 0,5) (z = f(1; 0,5) = 1/(0,5*1) = 2). Υπολογίστε την κλίση σε αυτό το σημείο
(-1/(1 2 *0,5); -1/(1*0,5 2)) = (-2; -4). Για να το απεικονίσουμε στο σχήμα 5.9, συνδέουμε το σημείο (1; 0.5) με το σημείο (-1; -3.5), επειδή (-1 - 1; -3.5 - 0.5) = (-2; - 4).

Ας πάρουμε έναν ακόμη πόντο στην ίδια γραμμή επιπέδου, αλλά μόνο τώρα σε ένα τέταρτο μη θετικών συντεταγμένων. Για παράδειγμα, σημείο (-0,5; -1) (z = f(-0,5; -1) = 1/((-1)*(-0,5)) = 2). Η κλίση σε αυτό το σημείο θα είναι
(-1/((-0,5) 2 *(-1)); -1/((-0,5)*(-1) 2)) = (4; 2). Ας το απεικονίσουμε στο Σχήμα 5.9 συνδέοντας το σημείο (-0.5; -1) με το σημείο (3.5; 1), επειδή (3.5 - (-0.5); 1 - (-1)) = (4 ; 2).

έννοια κατευθυντικό παράγωγο θεωρούνται για συναρτήσεις δύο και τριών μεταβλητών. Για να κατανοήσουμε την έννοια μιας κατευθυντικής παραγώγου, πρέπει να συγκρίνουμε τις παραγώγους εξ ορισμού.

Ως εκ τούτου,

Τώρα μπορούμε να βρούμε την παράγωγο προς την κατεύθυνση αυτής της συνάρτησης από τον τύπο της:

Και τώρα - εργασία. Δίνει μια συνάρτηση όχι τριών, αλλά μόνο δύο μεταβλητών, αλλά το διάνυσμα κατεύθυνσης δίνεται με λίγο διαφορετικό τρόπο. Πρέπει λοιπόν να επαναλάβετε διανυσματική άλγεβρα .

Παράδειγμα 2Να βρείτε την παράγωγο μιας συνάρτησης σε ένα σημείο Μ0 (1; 2) προς την κατεύθυνση του διανύσματος , όπου Μ1 - σημείο με συντεταγμένες (3; 0) .

Το διάνυσμα που καθορίζει την κατεύθυνση της παραγώγου μπορεί επίσης να δοθεί με τέτοια μορφή όπως στο ακόλουθο παράδειγμα - στη μορφή επεκτάσεις σε μοναδιαία διανύσματα αξόνων συντεταγμένων, αλλά αυτό είναι ένα οικείο θέμα από την αρχή της διανυσματικής άλγεβρας.

Παράδειγμα 3Να βρείτε την παράγωγο μιας συνάρτησης στο σημείο Μ0 (1; 1; 1) προς την κατεύθυνση του διανύσματος .

Λύση. Βρείτε τα συνημίτονα κατεύθυνσης του διανύσματος

Ας βρούμε μερικές παραγώγους συναρτήσεων σε ένα σημείο Μ0 :

Επομένως, μπορούμε να βρούμε την παράγωγο προς την κατεύθυνση αυτής της συνάρτησης από τον τύπο της:

κλίση συνάρτησης

Συνάρτηση κλίσης πολλών μεταβλητών σε ένα σημείο Μ0 χαρακτηρίζει την κατεύθυνση της μέγιστης ανάπτυξης αυτής της συνάρτησης στο σημείο Μ0 και το μέγεθος αυτής της μέγιστης ανάπτυξης.

Πώς να βρείτε την κλίση;

Ανάγκη ορισμού διάνυσμα του οποίου οι προβολές στους άξονες συντεταγμένωνείναι οι αξίες μερικώς παράγωγα, , αυτής της συνάρτησης στο αντίστοιχο σημείο:

Θα έπρεπε δηλαδή αναπαράσταση ενός διανύσματος από τα μοναδιαία διανύσματα των αξόνων συντεταγμένων, στο οποίο η μερική παράγωγος που αντιστοιχεί στον άξονά της πολλαπλασιάζεται με κάθε μοναδιαίο διάνυσμα.

Διάλεξη 15

Η διαβάθμιση μιας συνάρτησης δύο μεταβλητών και η κατευθυντική παράγωγος.

Ορισμός. Κλίση συνάρτησης

που ονομάζεται διάνυσμα

Όπως μπορείτε να δείτε από τον ορισμό της διαβάθμισης της συνάρτησης, οι συνιστώσες του διανύσματος διαβάθμισης είναι οι μερικές παράγωγοι της συνάρτησης.

Παράδειγμα. Υπολογισμός κλίσης συνάρτησης

στο σημείο Α(2,3).

Λύση. Υπολογίζουμε τις μερικές παραγώγους της συνάρτησης.

Γενικά, η διαβάθμιση της συνάρτησης έχει τη μορφή:

Αντικαταστήστε τις συντεταγμένες του σημείου Α(2,3) στις εκφράσεις των μερικών παραγώγων

Η κλίση συνάρτησης στο σημείο A(2,3) έχει τη μορφή:

Ομοίως, μπορούμε να ορίσουμε την έννοια της διαβάθμισης μιας συνάρτησης τριών μεταβλητών:

Ορισμός. Συνάρτηση κλίσης τριών μεταβλητών

που ονομάζεται διάνυσμα

Διαφορετικά, αυτό το διάνυσμα μπορεί να γραφτεί ως εξής:

Ορισμόςπαράγωγο κατεύθυνσης.

Έστω μια συνάρτηση δύο μεταβλητών

και ένα αυθαίρετο διάνυσμα

Θεωρήστε την αύξηση αυτής της συνάρτησης κατά μήκος του δεδομένου διανύσματος

Εκείνοι. το διάνυσμα είναι συγγραμμικό ως προς το διάνυσμα . Μήκος αύξησης επιχειρήματος

Η παράγωγος σε κάποια κατεύθυνση είναι το όριο του λόγου της αύξησης μιας συνάρτησης κατά μήκος μιας δεδομένης κατεύθυνσης προς το μήκος της αύξησης του ορίσματος, όταν το μήκος της αύξησης του ορίσματος τείνει στο 0.

Κατευθυντική Παράγωγος Τύπος.

Με βάση τον ορισμό της βαθμίδας, η παράγωγος μιας συνάρτησης ως προς την κατεύθυνση μπορεί να υπολογιστεί ως εξής.

κάποιο διάνυσμα. Ένα διάνυσμα με την ίδια κατεύθυνση αλλά μονόκλινοας πούμε το μήκος

Οι συντεταγμένες αυτού του διανύσματος υπολογίζονται ως εξής:

Από τον ορισμό της κατευθυντικής παραγώγου, η κατευθυντική παράγωγος μπορεί να υπολογιστεί χρησιμοποιώντας τον ακόλουθο τύπο:

Η δεξιά πλευρά αυτού του τύπου είναι το βαθμωτό γινόμενο δύο διανυσμάτων

Επομένως, η κατευθυντική παράγωγος μπορεί να αναπαρασταθεί ως ο ακόλουθος τύπος:

Αρκετές σημαντικές ιδιότητες του διανύσματος κλίσης απορρέουν από αυτόν τον τύπο.

Η πρώτη ιδιότητα μιας κλίσης προκύπτει από το προφανές γεγονός ότι το γινόμενο κουκίδων δύο διανυσμάτων είναι μεγαλύτερο όταν τα διανύσματα βρίσκονται στην ίδια κατεύθυνση. Η δεύτερη ιδιότητα προκύπτει από το γεγονός ότι το κλιμακωτό γινόμενο των κάθετων διανυσμάτων είναι ίσο με μηδέν. Επιπλέον, η γεωμετρική σημασία της κλίσης προκύπτει από την πρώτη ιδιότητα - η κλίση είναι ένα διάνυσμα κατά μήκος της κατεύθυνσης, του οποίου η παράγωγος κατά μήκος της κατεύθυνσης είναι η μεγαλύτερη. Εφόσον η κατευθυντική παράγωγος καθορίζει την εφαπτομένη της κλίσης της εφαπτομένης στην επιφάνεια της συνάρτησης, η κλίση κατευθύνεται κατά μήκος της μεγαλύτερης κλίσης της εφαπτομένης.

Παράδειγμα 2 Για μια συνάρτηση (από το παράδειγμα 1)

Υπολογίστε την κατευθυντική παράγωγο

στο σημείο Α(2,3).

Λύση. Για να υπολογίσετε την παράγωγο κατεύθυνσης, πρέπει να υπολογίσετε το διάνυσμα κλίσης στο καθορισμένο σημείο και το διάνυσμα διεύθυνσης μονάδας (δηλαδή, κανονικοποιήστε το διάνυσμα ).

Το διάνυσμα κλίσης υπολογίστηκε στο παράδειγμα 1:

Υπολογίστε το διάνυσμα διεύθυνσης μονάδας:

Υπολογίζουμε την παράγωγο προς την κατεύθυνση:

#2. Μέγιστο και ελάχιστο συνάρτησης πολλών μεταβλητών.

Ορισμός.Λειτουργία

Έχει ένα μέγιστο σε ένα σημείο (δηλαδή στο και ) εάν

Ορισμός.Με τον ίδιο ακριβώς τρόπο λέμε ότι η συνάρτηση

Έχει ένα ελάχιστο σε ένα σημείο (δηλαδή στο και ) εάν

για όλα τα σημεία αρκετά κοντά στο σημείο και διακριτά από αυτό.

Το μέγιστο και το ελάχιστο μιας συνάρτησης ονομάζονται άκρα της συνάρτησης, δηλαδή λένε ότι η συνάρτηση έχει άκρο σε ένα δεδομένο σημείο αν αυτή η συνάρτηση έχει μέγιστο ή ελάχιστο σε ένα δεδομένο σημείο.

Για παράδειγμα, η συνάρτηση

Έχει προφανές ελάχιστο z = -1 στο x = 1 και y = 2.

Έχει μέγιστο σε ένα σημείο x = 0 και y = 0.

Θεώρημα.(απαραίτητες ακραίες συνθήκες).

Εάν η συνάρτηση φτάσει σε ένα άκρο στο , τότε κάθε μερική παράγωγος πρώτης τάξης του z είτε εξαφανίζεται σε αυτές τις τιμές των ορισμάτων είτε δεν υπάρχει.

Σχόλιο.Αυτό το θεώρημα δεν επαρκεί για τη μελέτη του ζητήματος των ακραίων τιμών μιας συνάρτησης. Είναι δυνατόν να δώσουμε παραδείγματα συναρτήσεων που έχουν μηδενικές μερικές παραγώγους σε ορισμένα σημεία, αλλά δεν έχουν ακρότατο σε αυτά τα σημεία.

Παράδειγμα.Μια συνάρτηση που έχει μηδέν μερικές παραγώγους αλλά όχι ακρότατο.

Πράγματι:

Επαρκείς συνθήκες για εξτρέμ.

Θεώρημα.Έστω σε κάποια περιοχή που περιέχει το σημείο , η συνάρτηση έχει συνεχείς μερικές παραγώγους μέχρι την τρίτη τάξη συμπεριλαμβανομένων? ας είναι, επιπλέον, το σημείο ένα κρίσιμο σημείο της συνάρτησης, δηλ.

Στη συνέχεια στο,

Παράδειγμα 3.2. Εξετάστε τη συνάρτηση στο μέγιστο και στο ελάχιστο

Ας βρούμε τα κρίσιμα σημεία, δηλ. σημεία όπου οι πρώτες μερικές παράγωγοι είναι ίσες με μηδέν ή δεν υπάρχουν.

Αρχικά, υπολογίζουμε τις ίδιες τις μερικές παραγώγους.

Εξισώνουμε τις μερικές παραγώγους με το μηδέν και λύνουμε το ακόλουθο σύστημα γραμμικών εξισώσεων

Πολλαπλασιάστε τη δεύτερη εξίσωση επί 2 και προσθέστε την στην πρώτη. Παίρνετε μια εξίσωση μόνο από το y.

Βρείτε και αντικαταστήστε στην πρώτη εξίσωση

Ας μεταμορφωθούμε

Επομένως, το σημείο () είναι κρίσιμο.

Ας υπολογίσουμε τις δεύτερες παραγώγους της δεύτερης τάξης και ας αντικαταστήσουμε τις συντεταγμένες του κρίσιμου σημείου σε αυτές.

Στην περίπτωσή μας, δεν είναι απαραίτητο να αντικαταστήσουμε τις τιμές των κρίσιμων σημείων, καθώς οι δεύτερες παράγωγοι είναι αριθμοί.

Ως αποτέλεσμα, έχουμε:

Επομένως, το κρίσιμο σημείο που βρέθηκε είναι το ακραίο σημείο. Επιπλέον, από τότε

τότε αυτό είναι το ελάχιστο σημείο.

ΒαθμίδαΗ συνάρτηση gradz z=f(x 1 , x 2 , ... x n) είναι το διάνυσμα των μερικών παραγώγων της συνάρτησης σε ένα σημείο, δηλ. διάνυσμα με συντεταγμένες.

Εικόνα 5.8 - Διαβάθμιση της συνάρτησης z \u003d 2x 1 + x 2

Εξετάστε ένα άλλο παράδειγμα - τη συνάρτηση z= 1/(x 1 x 2). Η κλίση αυτής της συνάρτησης δεν θα είναι πλέον η ίδια σε διαφορετικά σημεία, αφού οι συντεταγμένες της καθορίζονται από τους τύπους (-1 / (x 1 2 x 2); -1 / (x 1 x 2 2)).

Το σχήμα 5.9 δείχνει τις γραμμές επιπέδου της συνάρτησης z= 1/(x 1 x 2) για τα επίπεδα 2 και 10 (η γραμμή 1/(x 1 x 2) = 2 υποδεικνύεται με μια διακεκομμένη γραμμή και η γραμμή 1/( x 1 x 2) = 10 είναι συμπαγής γραμμή).

Εικόνα 5.9 - Διαβαθμίσεις της συνάρτησης z \u003d 1 / (x 1 x 2) σε διάφορα σημεία

Πάρτε, για παράδειγμα, το σημείο (0,5; 1) και υπολογίστε τη διαβάθμιση σε αυτό το σημείο: (-1 / (0,5 2 * 1); -1 / (0,5 * 1 2)) \u003d (-4; - 2) . Σημειώστε ότι το σημείο (0,5; 1) βρίσκεται στη γραμμή επιπέδου 1 / (x 1 x 2) \u003d 2, επειδή z \u003d f (0,5; 1) \u003d 1 / (0,5 * 1) \u003d 2. Προς σχεδιάστε το διάνυσμα (-4; -2) στο σχήμα 5.9, συνδέστε το σημείο (0.5; 1) με το σημείο (-3.5; -1), επειδή (-3.5 - 0.5; -1 - 1) = (-4; -2).

Ας πάρουμε ένα άλλο σημείο στην ίδια ευθεία επιπέδου, για παράδειγμα, σημείο (1; 0,5) (z=f(1; 0,5) = 1/(0,5*1) = 2). Υπολογίστε τη διαβάθμιση σε αυτό το σημείο (-1/(1 2 *0,5); -1/(1*0,5 2)) = (-2; -4). Για να το απεικονίσουμε στο σχήμα 5.9, συνδέουμε το σημείο (1; 0.5) με το σημείο (-1; -3.5), επειδή (-1 - 1; -3.5 - 0.5) = (-2; - 4).

Ας πάρουμε έναν ακόμη πόντο στην ίδια γραμμή επιπέδου, αλλά μόνο τώρα σε ένα τέταρτο μη θετικών συντεταγμένων. Για παράδειγμα, σημείο (-0,5; -1) (z=f(-0,5; -1) = 1/((-1)*(-0,5)) = 2). Η κλίση σε αυτό το σημείο θα είναι (-1/((-0.5) 2 *(-1)); -1/((-0.5)*(-1) 2)) = (4; 2). Ας το απεικονίσουμε στο Σχήμα 5.9 συνδέοντας το σημείο (-0.5; -1) με το σημείο (3.5; 1), επειδή (3.5 - (-0.5); 1 - (-1)) = (4 ; 2).

Πρέπει να σημειωθεί ότι και στις τρεις περιπτώσεις που εξετάστηκαν, η διαβάθμιση δείχνει την κατεύθυνση ανάπτυξης του επιπέδου της συνάρτησης (προς τη γραμμή επιπέδου 1/(x 1 x 2) = 10 > 2).

Μπορεί να αποδειχθεί ότι η κλίση είναι πάντα κάθετη στη γραμμή στάθμης (επίπεδη επιφάνεια) που διέρχεται από το δεδομένο σημείο.

Ακραία συνάρτησης πολλών μεταβλητών

Ας ορίσουμε την έννοια ακραίογια μια συνάρτηση πολλών μεταβλητών.

Η συνάρτηση πολλών μεταβλητών f(X) έχει στο σημείο X (0) μέγιστο (ελάχιστο),αν υπάρχει τέτοια γειτονιά αυτού του σημείου ώστε για όλα τα σημεία Χ από αυτή τη γειτονιά να ισχύουν οι ανισώσεις f(X)f(X (0)) ().

Εάν αυτές οι ανισότητες ικανοποιηθούν ως αυστηρές, τότε ονομάζεται ακρότατο ισχυρός, και αν όχι, τότε αδύναμος.

Σημειώστε ότι το άκρο που ορίζεται με αυτόν τον τρόπο είναι τοπικόςχαρακτήρα, αφού αυτές οι ανισότητες ισχύουν μόνο για κάποια γειτονιά του ακραίου σημείου.

Απαραίτητη προϋπόθεση για ένα τοπικό άκρο μιας διαφοροποιήσιμης συνάρτησης z=f(x 1, . . ., x n) σε ένα σημείο είναι η ισότητα προς το μηδέν όλων των μερικών παραγώγων πρώτης τάξης σε αυτό το σημείο:
.

Τα σημεία στα οποία ισχύουν αυτές οι ισότητες ονομάζονται ακίνητος.

Με έναν άλλο τρόπο, η απαραίτητη συνθήκη για ένα ακρότατο μπορεί να διατυπωθεί ως εξής: στο ακραίο σημείο, η κλίση είναι ίση με μηδέν. Είναι επίσης δυνατό να αποδειχθεί μια γενικότερη δήλωση - στο ακραίο σημείο, οι παράγωγοι της συνάρτησης εξαφανίζονται προς όλες τις κατευθύνσεις.

Τα σταθερά σημεία θα πρέπει να υποβληθούν σε πρόσθετες μελέτες - εάν πληρούνται επαρκείς προϋποθέσεις για την ύπαρξη τοπικού άκρου. Για να το κάνετε αυτό, καθορίστε το πρόσημο του διαφορικού δεύτερης τάξης. Αν για οποιαδήποτε που δεν είναι ταυτόχρονα ίση με μηδέν, είναι πάντα αρνητική (θετική), τότε η συνάρτηση έχει μέγιστο (ελάχιστο). Εάν μπορεί να εξαφανιστεί όχι μόνο με μηδενικές προσαυξήσεις, τότε το ζήτημα του άκρου παραμένει ανοιχτό. Εάν μπορεί να λάβει και θετικές και αρνητικές τιμές, τότε δεν υπάρχει ακρότατο στο ακίνητο σημείο.

Στη γενική περίπτωση, ο προσδιορισμός του πρόσημου του διαφορικού είναι ένα αρκετά περίπλοκο πρόβλημα, το οποίο δεν θα εξετάσουμε εδώ. Για μια συνάρτηση δύο μεταβλητών, μπορεί κανείς να αποδείξει ότι αν βρίσκεται σε ακίνητο σημείο
, τότε υπάρχει ένα άκρο. Στην περίπτωση αυτή, το πρόσημο του δεύτερου διαφορικού συμπίπτει με το πρόσημο
, δηλ. αν
, τότε αυτό είναι το μέγιστο, και αν
, τότε αυτό είναι το ελάχιστο. Αν
, τότε δεν υπάρχει ακρότατο σε αυτό το σημείο, και αν
, τότε το ζήτημα του εξτρέμ παραμένει ανοιχτό.

Παράδειγμα 1. Βρείτε τα άκρα μιας συνάρτησης
.

Ας βρούμε μερικές παραγώγους με τη μέθοδο της λογαριθμικής διαφοροποίησης.

ln z = ln 2 + ln (x + y) + ln (1 + xy) – ln (1 + x 2) – ln (1 + y 2)

Ομοίως
.

Ας βρούμε στάσιμα σημεία από το σύστημα των εξισώσεων:

Έτσι, βρίσκονται τέσσερα ακίνητα σημεία (1; 1), (1; -1), (-1; 1) και (-1; -1).

Ας βρούμε μερικές παραγώγους δεύτερης τάξης:

ln (z x `) = ln 2 + ln (1 - x 2) -2ln (1 + x 2)

Ομοίως
;
.

Επειδή
, σημάδι έκφρασης
εξαρτάται μόνο από
. Σημειώστε ότι και στις δύο αυτές παραγώγους ο παρονομαστής είναι πάντα θετικός, επομένως μπορείτε να λάβετε υπόψη μόνο το πρόσημο του αριθμητή ή ακόμα και το πρόσημο των παραστάσεων x (x 2 - 3) και y (y 2 - 3). Ας το προσδιορίσουμε σε κάθε κρίσιμο σημείο και ας ελέγξουμε την εκπλήρωση της επαρκούς ακραίας συνθήκης.

Για το σημείο (1; 1) παίρνουμε 1*(1 2 - 3) = -2< 0. Т.к. произведение двух отрицательных чисел
> 0, και
< 0, в точке (1; 1) можно найти максимум. Он равен
= 2*(1 + 1)*(1 +1*1)/((1 +1 2)*(1 +1 2)) = = 8/4 = 2.

Για το σημείο (1; -1) παίρνουμε 1*(1 2 - 3) = -2< 0 и (-1)*((-1) 2 – 3) = 2 >0. Επειδή το γινόμενο αυτών των αριθμών
< 0, в этой точке экстремума нет. Аналогично можно показать, что нет экстремума в точке (-1; 1).

Για το σημείο (-1; -1) παίρνουμε (-1)*((-1) 2 - 3) = 2 > 0. γινόμενο δύο θετικών αριθμών
> 0, και
> 0, στο σημείο (-1; -1) μπορείτε να βρείτε ένα ελάχιστο. Είναι ίσο με 2*((-1) + (-1))*(1 +(-1)*(-1))/((1 +(-1) 2)*(1 +(-1) 2) ) = -8/4 = = -2.

Εύρημα παγκόσμιατο μέγιστο ή το ελάχιστο (η μεγαλύτερη ή η μικρότερη τιμή της συνάρτησης) είναι κάπως πιο περίπλοκο από το τοπικό άκρο, καθώς αυτές οι τιμές μπορούν να επιτευχθούν όχι μόνο σε σταθερά σημεία, αλλά και στο όριο του τομέα ορισμού. Δεν είναι πάντα εύκολο να μελετήσουμε τη συμπεριφορά μιας συνάρτησης στο όριο αυτής της περιοχής.

Σύντομη θεωρία

Κλίση είναι ένα διάνυσμα του οποίου η κατεύθυνση δείχνει την κατεύθυνση της ταχύτερης αύξησης στη συνάρτηση f(x). Η εύρεση αυτής της διανυσματικής ποσότητας συνδέεται με τον ορισμό των μερικών παραγώγων της συνάρτησης. Η κατευθυντική παράγωγος είναι μια βαθμωτή τιμή και δείχνει τον ρυθμό μεταβολής της συνάρτησης όταν κινείται κατά μήκος της κατεύθυνσης που δίνεται από κάποιο διάνυσμα.

Παράδειγμα λύσης προβλήματος

Το έργο

Δίνεται συνάρτηση , σημείο και διάνυσμα . Εύρημα:

Η λύση του προβλήματος

Εύρεση της κλίσης μιας συνάρτησης

1) Βρείτε τη διαβάθμιση της συνάρτησης στο σημείο :

Επιθυμητή κλίση:

Εύρεση της παραγώγου ως προς την κατεύθυνση ενός διανύσματος

2) Βρείτε την παράγωγο προς την κατεύθυνση του διανύσματος:

όπου είναι η γωνία που σχηματίζεται από το διάνυσμα και τον άξονα

Επιθυμητή παράγωγος στο σημείο:

Η τιμή επηρεάζεται έντονα από τον επείγοντα χαρακτήρα της απόφασης (από ημέρες έως αρκετές ώρες). Η ηλεκτρονική βοήθεια στις εξετάσεις / τεστ πραγματοποιείται κατόπιν ραντεβού.

Η εφαρμογή μπορεί να μείνει απευθείας στη συνομιλία, έχοντας προηγουμένως απορρίψει την κατάσταση των εργασιών και ενημερώνοντάς σας για τις προθεσμίες επίλυσής της. Ο χρόνος απόκρισης είναι αρκετά λεπτά.