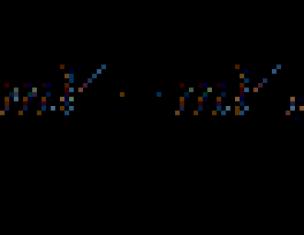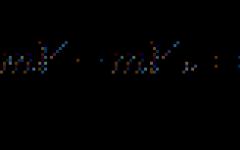Απόσταση μεταξύ σημείων 6. Απόσταση μεταξύ δύο σημείων. Απόσταση μεταξύ δύο σημείων σε μια γραμμή συντεταγμένων

Ας δοθεί ένα ορθογώνιο σύστημα συντεταγμένων.

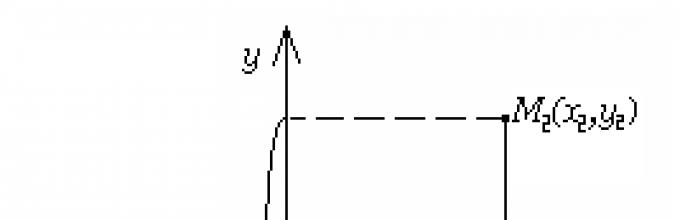
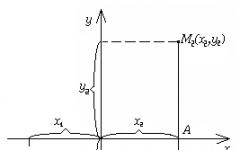
Θεώρημα 1.1.Για οποιαδήποτε δύο σημεία M 1 (x 1, y 1) και M 2 (x 2, y 2) του επιπέδου, η απόσταση d μεταξύ τους εκφράζεται με τον τύπο

Απόδειξη.Ας ρίξουμε από τα σημεία M 1 και M 2 τις κάθετες M 1 B και M 2 A, αντίστοιχα

στους άξονες Oy και Ox και να συμβολίσετε με K το σημείο τομής των ευθειών M 1 B και M 2 A (Εικ. 1.4). Είναι δυνατές οι ακόλουθες περιπτώσεις:

1) Τα σημεία M 1, M 2 και K είναι διαφορετικά. Προφανώς, το σημείο Κ έχει συντεταγμένες (x 2, y 1). Είναι εύκολο να δούμε ότι M 1 K = ôx 2 – x 1 ô, M 2 K = ôy 2 – y 1 ô. Επειδή ∆M 1 KM 2 είναι ορθογώνιο, τότε από το Πυθαγόρειο θεώρημα d = M 1 M 2 = = .

2) Το σημείο K συμπίπτει με το σημείο M 2, αλλά είναι διαφορετικό από το σημείο M 1 (Εικ. 1.5). Σε αυτή την περίπτωση y 2 = y 1

και d \u003d M 1 M 2 \u003d M 1 K \u003d ôx 2 - x 1 ô \u003d =

3) Το σημείο Κ συμπίπτει με το σημείο Μ 1, αλλά είναι διαφορετικό από το σημείο Μ 2. Σε αυτή την περίπτωση x 2 = x 1 και d =

M 1 M 2 \u003d KM 2 \u003d ôy 2 - y 1 ô \u003d = .

4) Το σημείο M 2 συμπίπτει με το σημείο M 1. Στη συνέχεια x 1 \u003d x 2, y 1 \u003d y 2 και

d \u003d M 1 M 2 \u003d O \u003d.

Η διαίρεση του τμήματος ως προς αυτό.

Έστω ένα αυθαίρετο τμήμα M 1 M 2 στο επίπεδο και έστω M οποιοδήποτε σημείο αυτού

τμήμα διαφορετικό από το σημείο M 2 (Εικ. 1.6). Ο αριθμός l που ορίζεται από την ισότητα l = , λέγεται στάση,στο οποίο το σημείο M διαιρεί το τμήμα M 1 M 2.

Θεώρημα 1.2.Εάν το σημείο M (x; y) διαιρεί το τμήμα M 1 M 2 σε σχέση με το l, τότε οι συντεταγμένες αυτού καθορίζονται από τους τύπους

x = , y = , (4)

όπου (x 1; y 1) είναι οι συντεταγμένες του σημείου M 1, (x 2; y 2) είναι οι συντεταγμένες του σημείου M 2.

Απόδειξη.Ας αποδείξουμε τον πρώτο από τους τύπους (4). Ο δεύτερος τύπος αποδεικνύεται παρόμοια. Δύο περιπτώσεις είναι πιθανές.

x = x 1 = = = .

2) Η ευθεία M 1 M 2 δεν είναι κάθετη στον άξονα Ox (Εικ. 1.6). Ας ρίξουμε τις κάθετες από τα σημεία M 1 , M, M 2 στον άξονα Ox και δηλώνουμε τα σημεία τομής τους με τον άξονα Ox αντίστοιχα P 1 , P, P 2 . Σύμφωνα με το θεώρημα των αναλογικών τμημάτων =l.

Επειδή P 1 P \u003d ôx - x 1 ô, PP 2 \u003d ôx 2 - xô και οι αριθμοί (x - x 1) και (x 2 - x) έχουν το ίδιο πρόσημο (για x 1< х 2 они положительны, а при х 1 >x 2 είναι αρνητικά), τότε

l == ,

x - x 1 \u003d l (x 2 - x), x + lx \u003d x 1 + lx 2,

x = .

Συμπέρασμα 1.2.1.Αν τα M 1 (x 1; y 1) και M 2 (x 2; y 2) είναι δύο αυθαίρετα σημεία και το σημείο M (x; y) είναι το μέσο του τμήματος M 1 M 2, τότε

x = , y = (5)

Απόδειξη.Αφού M 1 M = M 2 M, τότε l = 1 και με τους τύπους (4) λαμβάνουμε τους τύπους (5).

Εμβαδόν τριγώνου.

Θεώρημα 1.3.Για οποιαδήποτε σημεία A (x 1; y 1), B (x 2; y 2) και C (x 3; y 3) που δεν βρίσκονται στο ίδιο

ευθεία, το εμβαδόν S του τριγώνου ABC εκφράζεται με τον τύπο

S \u003d ô (x 2 - x 1) (y 3 - y 1) - (x 3 - x 1) (y 2 - y 1) ô (6)

Απόδειξη.Η περιοχή Δ ABC που φαίνεται στο σχ. 1.7, υπολογίζουμε ως εξής

S ABC \u003d S ADEC + S BCEF - S ABFD.

Υπολογίστε το εμβαδόν του τραπεζοειδούς:

S-ADEC=
,

SBCEF=

S ABFD =

Τώρα έχουμε

S ABC \u003d ((x 3 - x 1) (y 3 + y 1) + (x 3 - x 2) (y 3 + y 2) - (x 2 - -x 1) (y 1 + y 2) ) \u003d (x 3 y 3 - x 1 y 3 + x 3 y 1 - x 1 y 1 + + x 2 y 3 - -x 3 y 3 + x 2 y 2 - x 3 y 2 - x 2 y 1 + x 1 y 1 - x 2 y 2 + x 1 y 2) \u003d (x 3 y 1 - x 3 y 2 + x 1 y 2 - x 2 y 1 + x 2 y 3 -

X 1 y 3) \u003d (x 3 (y 1 - y 2) + x 1 y 2 - x 1 y 1 + x 1 y 1 - x 2 y 1 + y 3 (x 2 - x 1)) \u003d (x 1 (y 2 - y 1) - x 3 (y 2 - y 1) + + y 1 (x 1 - x 2) - y 3 (x 1 - x 2)) \u003d ((x 1 - x 3) ( y 2 - y 1) + (x 1 - x 2) (y 1 - y 3)) \u003d ((x 2 - x 1) (y 3 - y 1) -

- (x 3 - x 1) (y 2 - y 1)).

Για μια άλλη θέση ∆ ABC, ο τύπος (6) αποδεικνύεται παρόμοια, αλλά μπορεί να ληφθεί με το πρόσημο «-». Επομένως, στον τύπο (6) βάλτε το πρόσημο του συντελεστή.

Διάλεξη 2

Η εξίσωση μιας ευθείας γραμμής σε ένα επίπεδο: η εξίσωση μιας ευθείας γραμμής με τον κύριο συντελεστή, η γενική εξίσωση μιας ευθείας γραμμής, η εξίσωση μιας ευθείας γραμμής σε τμήματα, η εξίσωση μιας ευθείας που διέρχεται από δύο σημεία. Γωνία μεταξύ ευθειών, συνθήκες παραλληλισμού και καθετότητας ευθειών σε επίπεδο.

2.1. Ας δοθεί ένα ορθογώνιο σύστημα συντεταγμένων και κάποια ευθεία L στο επίπεδο.

Ορισμός 2.1.Μια εξίσωση της μορφής F(x;y) = 0 που συσχετίζει τις μεταβλητές x και y ονομάζεται εξίσωση γραμμής L(σε ένα δεδομένο σύστημα συντεταγμένων) εάν αυτή η εξίσωση ικανοποιείται από τις συντεταγμένες οποιουδήποτε σημείου που βρίσκεται στην ευθεία L και όχι από τις συντεταγμένες οποιουδήποτε σημείου που δεν βρίσκεται σε αυτήν την ευθεία.

Παραδείγματα εξισώσεων ευθειών σε επίπεδο.

1) Θεωρούμε μια ευθεία παράλληλη προς τον άξονα Oy ενός ορθογώνιου συστήματος συντεταγμένων (Εικ. 2.1). Ας υποδηλώσουμε με το γράμμα Α το σημείο τομής αυτής της ευθείας με τον άξονα Ox, (a; o) ─ της ή-

dinats. Η εξίσωση x = a είναι η εξίσωση της δεδομένης ευθείας. Πράγματι, αυτή η εξίσωση ικανοποιείται από τις συντεταγμένες οποιουδήποτε σημείου M(a; y) αυτής της ευθείας και όχι από τις συντεταγμένες οποιουδήποτε σημείου που δεν βρίσκεται στην ευθεία. Αν a = 0, τότε η ευθεία συμπίπτει με τον άξονα Oy, ο οποίος έχει την εξίσωση x = 0.

2) Η εξίσωση x - y \u003d 0 ορίζει το σύνολο των σημείων στο επίπεδο που αποτελούν τις διχοτόμους των γωνιών συντεταγμένων I και III.

3) Η εξίσωση x 2 - y 2 \u003d 0 είναι η εξίσωση δύο διχοτόμων γωνιών συντεταγμένων.

4) Η εξίσωση x 2 + y 2 = 0 ορίζει ένα μόνο σημείο O(0;0) στο επίπεδο.

5) Η εξίσωση x 2 + y 2 \u003d 25 είναι η εξίσωση ενός κύκλου ακτίνας 5 με κέντρο στην αρχή.

Οι συντεταγμένες καθορίζουν τη θέση ενός αντικειμένου στην υδρόγειο. Οι συντεταγμένες υποδεικνύονται με γεωγραφικό πλάτος και γεωγραφικό μήκος. Τα γεωγραφικά πλάτη μετρώνται από τη γραμμή του ισημερινού και στις δύο πλευρές. Στο βόρειο ημισφαίριο τα γεωγραφικά πλάτη είναι θετικά, στο νότιο ημισφαίριο είναι αρνητικά. Το γεωγραφικό μήκος μετράται από τον αρχικό μεσημβρινό είτε προς τα ανατολικά είτε προς τα δυτικά, αντίστοιχα, προκύπτει είτε ανατολικό είτε δυτικό γεωγραφικό μήκος.

Σύμφωνα με τη γενικά αποδεκτή θέση, ως αρχικός λαμβάνεται ο μεσημβρινός, ο οποίος διέρχεται από το παλιό Αστεροσκοπείο του Γκρίνουιτς στο Γκρίνουιτς. Οι γεωγραφικές συντεταγμένες της τοποθεσίας μπορούν να ληφθούν χρησιμοποιώντας έναν πλοηγό GPS. Αυτή η συσκευή λαμβάνει σήματα από ένα δορυφορικό σύστημα εντοπισμού θέσης στο σύστημα συντεταγμένων WGS-84, το ίδιο για ολόκληρο τον κόσμο.

Τα μοντέλα Navigator διαφέρουν ως προς τους κατασκευαστές, τη λειτουργικότητα και τη διεπαφή. Επί του παρόντος, οι ενσωματωμένοι πλοηγοί GPS είναι διαθέσιμοι σε ορισμένα μοντέλα κινητών τηλεφώνων. Αλλά οποιοδήποτε μοντέλο μπορεί να καταγράψει και να αποθηκεύσει συντεταγμένες σημείων.

Απόσταση μεταξύ συντεταγμένων GPS

Για την επίλυση πρακτικών και θεωρητικών προβλημάτων σε ορισμένες βιομηχανίες, είναι απαραίτητο να μπορούμε να προσδιορίζουμε τις αποστάσεις μεταξύ των σημείων από τις συντεταγμένες τους. Για να το κάνετε αυτό, μπορείτε να χρησιμοποιήσετε διάφορες μεθόδους. Κανονική αναπαράσταση γεωγραφικών συντεταγμένων: μοίρες, λεπτά, δευτερόλεπτα.

Για παράδειγμα, μπορείτε να προσδιορίσετε την απόσταση μεταξύ των ακόλουθων συντεταγμένων: σημείο Νο. 1 - γεωγραφικό πλάτος 55°45′07″ Β, γεωγραφικό μήκος 37°36′56″ Α. σημείο Νο. 2 - γεωγραφικό πλάτος 58°00′02″ Β, γεωγραφικό μήκος 102°39′42″ Α

Ο ευκολότερος τρόπος είναι να χρησιμοποιήσετε μια αριθμομηχανή για να υπολογίσετε την απόσταση μεταξύ δύο σημείων. Στη μηχανή αναζήτησης του προγράμματος περιήγησης, πρέπει να ορίσετε τις ακόλουθες παραμέτρους αναζήτησης: online - για να υπολογίσετε την απόσταση μεταξύ δύο συντεταγμένων. Στην ηλεκτρονική αριθμομηχανή, οι τιμές γεωγραφικού πλάτους και μήκους εισάγονται στα πεδία ερωτήματος για την πρώτη και τη δεύτερη συντεταγμένη. Κατά τον υπολογισμό, η ηλεκτρονική αριθμομηχανή έδωσε το αποτέλεσμα - 3.800.619 m.

Η επόμενη μέθοδος είναι πιο χρονοβόρα, αλλά και πιο οπτική. Είναι απαραίτητο να χρησιμοποιήσετε οποιοδήποτε διαθέσιμο πρόγραμμα χαρτογράφησης ή πλοήγησης. Τα προγράμματα στα οποία μπορείτε να δημιουργήσετε σημεία ανά συντεταγμένες και να μετρήσετε τις αποστάσεις μεταξύ τους περιλαμβάνουν τις ακόλουθες εφαρμογές: BaseCamp (ένα σύγχρονο ανάλογο του προγράμματος MapSource), Google Earth, SAS.Planet.

Όλα τα παραπάνω προγράμματα είναι διαθέσιμα σε οποιονδήποτε χρήστη του δικτύου. Για παράδειγμα, για να υπολογίσετε την απόσταση μεταξύ δύο συντεταγμένων στο Google Earth, πρέπει να δημιουργήσετε δύο ετικέτες που να δείχνουν τις συντεταγμένες του πρώτου σημείου και του δεύτερου σημείου. Στη συνέχεια, χρησιμοποιώντας το εργαλείο "Χάρακας", πρέπει να συνδέσετε το πρώτο και το δεύτερο σημάδι με μια γραμμή, το πρόγραμμα θα δώσει αυτόματα το αποτέλεσμα της μέτρησης και θα δείξει τη διαδρομή στη δορυφορική εικόνα της Γης.

Στην περίπτωση του παραπάνω παραδείγματος, το πρόγραμμα Google Earth επέστρεψε το αποτέλεσμα - το μήκος της απόστασης μεταξύ του σημείου #1 και του σημείου #2 είναι 3.817.353 m.

Γιατί υπάρχει λάθος στον προσδιορισμό της απόστασης

Όλοι οι υπολογισμοί απόστασης μεταξύ των συντεταγμένων βασίζονται σε υπολογισμούς μήκους τόξου. Η ακτίνα της Γης εμπλέκεται στον υπολογισμό του μήκους του τόξου. Επειδή όμως το σχήμα της Γης είναι κοντά σε ένα λοξό ελλειψοειδές, η ακτίνα της Γης σε ορισμένα σημεία είναι διαφορετική. Για τον υπολογισμό της απόστασης μεταξύ των συντεταγμένων, λαμβάνεται η μέση τιμή της ακτίνας της Γης, η οποία δίνει σφάλμα στη μέτρηση. Όσο μεγαλύτερη είναι η μετρούμενη απόσταση, τόσο μεγαλύτερο είναι το σφάλμα.

Let , (Εικόνα 2.3). Απαιτείται να βρεθεί.

Εικόνα 2.3. Η απόσταση μεταξύ δύο σημείων.

Από ορθογώνιο από το Πυθαγόρειο θεώρημα έχουμε

Αυτό είναι ,

Αυτός ο τύπος ισχύει για οποιαδήποτε διάταξη σημείων και .

II. Η διαίρεση του τμήματος ως προς αυτό:

Αφήστε , . Απαιτείται να βρεθεί η ξαπλωμένη στο τμήμα και να διαιρεθεί σε αυτή την αναλογία (Εικόνα 2.4.).

Εικόνα 2.4. Η διαίρεση του τμήματος ως προς αυτό.

Από ομοιότητα ~ , δηλαδή , από πού . Επίσης.

Με αυτόν τον τρόπο,

- ο τύπος για τη διαίρεση ενός τμήματος σε σχέση με .

Αν τότε

είναι οι συντεταγμένες του μέσου του τμήματος.

Σχόλιο.Οι παραγόμενοι τύποι μπορούν επίσης να γενικευτούν στην περίπτωση ενός χωρικού ορθογώνιου καρτεσιανού συστήματος συντεταγμένων. Αφήστε σημεία , . Τότε

- τύπος για την εύρεση της απόστασης μεταξύ σημείων και .

Ο τύπος για τη διαίρεση ενός τμήματος σε σχέση με .

Εκτός από το καρτεσιανό στο επίπεδο και στο διάστημα, μπορείτε να δημιουργήσετε έναν μεγάλο αριθμό άλλων συστημάτων συντεταγμένων, δηλαδή τρόπους για να χαρακτηρίσετε τη θέση ενός σημείου σε ένα επίπεδο ή στο διάστημα χρησιμοποιώντας δύο ή τρεις αριθμητικές παραμέτρους (συντεταγμένες). Εξετάστε μερικά από τα υπάρχοντα συστήματα συντεταγμένων.

Σε ένα αεροπλάνο, μπορεί κανείς να ορίσει πολικό σύστημα συντεταγμένων , που χρησιμοποιείται, ειδικότερα, στη μελέτη περιστροφικών κινήσεων.

Εικόνα 2.5. Πολικό σύστημα συντεταγμένων.

Καθορίζουμε ένα σημείο στο επίπεδο και μια μισή γραμμή που αναδύεται από αυτό, και επίσης επιλέγουμε μια μονάδα κλίμακας (Εικόνα 2.5). Το σημείο λέγεται Πόλος , μισή γραμμή - πολικός άξονας . Ας αντιστοιχίσουμε δύο αριθμούς σε ένα αυθαίρετο σημείο:

– πολική ακτίνα , ίση με την απόσταση από το σημείο M έως τον πόλο O.

– πολική γωνία , ίση με τη γωνία μεταξύ του πολικού άξονα και της ημιευθείας.

Μετρούμενη σε ακτίνια, η μέτρηση της θετικής κατεύθυνσης των τιμών είναι από αριστερόστροφα, συνήθως θεωρείται ότι είναι .

Ο πόλος αντιστοιχεί στην πολική ακτίνα, η πολική γωνία για αυτόν δεν έχει οριστεί.

Ας βρούμε τη σχέση μεταξύ ορθογωνικών και πολικών συντεταγμένων (Εικόνα 2.6).

Εικόνα 2.6. Σχέση ορθογώνιων και πολικών συστημάτων συντεταγμένων.

Θα θεωρήσουμε την αρχή του ορθογώνιου συστήματος συντεταγμένων ως πόλο και θα πάρουμε τη δέσμη ως πολικό άξονα. Έστω - σε ένα ορθογώνιο καρτεσιανό σύστημα συντεταγμένων και - σε ένα πολικό σύστημα συντεταγμένων. Βρείτε τη σχέση μεταξύ ορθογώνιων και πολικών συντεταγμένων.

Από ορθογώνιο, και από ορθογώνιο. Οι τύποι λοιπόν

εκφράζουν τις ορθογώνιες συντεταγμένες ενός σημείου ως προς τις πολικές συντεταγμένες του.

Η αντίστροφη σχέση εκφράζεται με τους τύπους

Σχόλιο.Η πολική γωνία μπορεί επίσης να προσδιοριστεί από τον τύπο, αφού προηγουμένως είχε προσδιοριστεί με ορθογώνιες συντεταγμένες σε ποιο τέταρτο βρίσκεται το σημείο.

Παράδειγμα 1Βρείτε τις πολικές συντεταγμένες του σημείου .

Λύση.Υπολογίστε ; Η πολική γωνία βρίσκεται από τις συνθήκες:

Επομένως, , επομένως .

Παράδειγμα 2Να βρείτε τις ορθογώνιες συντεταγμένες του σημείου .

Λύση.Υπολογίζω

Παίρνουμε .

Στον τρισδιάστατο χώρο, εκτός από το ορθογώνιο καρτεσιανό σύστημα συντεταγμένων, χρησιμοποιούνται συχνά κυλινδρικά και σφαιρικά συστήματα συντεταγμένων.

Κυλινδρικό σύστημα συντεταγμένωνείναι ένα πολικό σύστημα συντεταγμένων στο επίπεδο , στο οποίο προστίθεται ο χωρικός άξονας, κάθετα σε αυτό το επίπεδο (Εικόνα 2.7). Η θέση οποιουδήποτε σημείου χαρακτηρίζεται από τρεις αριθμούς - τις κυλινδρικές συντεταγμένες του: , όπου και είναι οι πολικές συντεταγμένες (πολική ακτίνα και πολική γωνία) της προβολής του σημείου στο επίπεδο στο οποίο επιλέγεται το πολικό σύστημα συντεταγμένων, - η εφαρμογή , που ισούται με την απόσταση από το σημείο μέχρι το καθορισμένο επίπεδο.

Εικόνα 2.7. Κυλινδρικό σύστημα συντεταγμένων

Για να καθορίσουμε τη σχέση μεταξύ του ορθογώνιου καρτεσιανού συστήματος συντεταγμένων και του κυλινδρικού συστήματος συντεταγμένων, θα τα τακτοποιήσουμε το ένα ως προς το άλλο όπως στο σχήμα 2.8 (θα τοποθετήσουμε το επίπεδο στο επίπεδο και ο πολικός άξονας συμπίπτει με τη θετική κατεύθυνση του άξονα , ο άξονας είναι κοινός και στα δύο συστήματα συντεταγμένων).

Αφήνω να είναι οι ορθογώνιες συντεταγμένες του σημείου , να είναι οι κυλινδρικές συντεταγμένες αυτού του σημείου και να είναι η προβολή του σημείου στο επίπεδο . Τότε

τύποι που σχετίζονται με ορθογώνιες και κυλινδρικές συντεταγμένες ενός σημείου.

Εικόνα 2.8. Σχέση ορθογώνιου καρτεσιανού

και κυλινδρικά συστήματα συντεταγμένων

Σχόλιο.Οι κυλινδρικές συντεταγμένες χρησιμοποιούνται συχνά όταν εξετάζουμε σώματα περιστροφής και ο άξονας βρίσκεται κατά μήκος του άξονα περιστροφής.

Σφαιρικό σύστημα συντεταγμένωνμπορεί να κατασκευαστεί με τον ακόλουθο τρόπο. Επιλέγουμε τον πολικό άξονα στο επίπεδο. Μέσα από το σημείο τραβάμε μια ευθεία κάθετη στο επίπεδο (κανονική). Τότε οποιοδήποτε σημείο στο χώρο μπορεί να συσχετιστεί με τρεις πραγματικούς αριθμούς, όπου είναι η απόσταση από το σημείο έως, είναι η γωνία μεταξύ του άξονα και η προβολή του τμήματος στο επίπεδο, είναι η γωνία μεταξύ του κανονικού και του τμήματος. Σημειώσε ότι , , .

Εάν τοποθετήσουμε το επίπεδο στο επίπεδο και επιλέξουμε τον πολικό άξονα που συμπίπτει με τη θετική κατεύθυνση του άξονα, επιλέξουμε τον άξονα ως κανονικό (Εικόνα 2.9), τότε λαμβάνουμε τύπους που συνδέουν αυτά τα δύο συστήματα συντεταγμένων

Εικόνα 2.9. Σχέση μεταξύ σφαιρικού και ορθογώνιου καρτεσιανού

συστήματα συντεταγμένων

σκαλοπάτια,ή βαθμωτών χαρακτηρίζονται πλήρως από την αριθμητική τους αξία στο επιλεγμένο σύστημα μονάδων. Διανυσματικές ποσότητες ή διανύσματα, εκτός από αριθμητική τιμή, έχουν και διεύθυνση. Για παράδειγμα, αν πούμε ότι ο άνεμος φυσά με ταχύτητα 10 m/s, τότε θα εισαγάγουμε την κλιμακωτή τιμή της ταχύτητας του ανέμου, αλλά αν πούμε ότι ο νοτιοδυτικός άνεμος φυσά με ταχύτητα 10 m/s , τότε σε αυτήν την περίπτωση η ταχύτητα του ανέμου θα είναι ήδη διάνυσμα.

Διάνυσμαονομάζεται ένα κατευθυνόμενο τμήμα, που έχει ορισμένο μήκος, δηλ. ένα τμήμα συγκεκριμένου μήκους, στο οποίο ένα από τα περιοριστικά σημεία λαμβάνεται ως αρχή και το δεύτερο ως τέλος. Το διάνυσμα θα συμβολίζεται είτε , είτε (Εικόνα 2.10).

Το μήκος ενός διανύσματος συμβολίζεται με το σύμβολο ή και ονομάζεται συντελεστής του διανύσματος. Ένα διάνυσμα του οποίου το μήκος είναι 1 ονομάζεται μονόκλινο . Το διάνυσμα ονομάζεται μηδέν , αν η αρχή και το τέλος του συμπίπτουν και συμβολίζεται με θ ή . Το μηδενικό διάνυσμα δεν έχει καθορισμένη κατεύθυνση και έχει μήκος ίσο με μηδέν. Τα διανύσματα που βρίσκονται στην ίδια ευθεία ή σε παράλληλες ευθείες ονομάζονται συγγραμμική . Δύο διανύσματα και λέγονται ίσος αν είναι συγγραμμικά, έχουν το ίδιο μήκος και την ίδια κατεύθυνση. Όλα τα μηδενικά διανύσματα θεωρούνται ίσα.

Καλούνται δύο μη μηδενικά συγγραμμικά διανύσματα που έχουν ίσο μέτρο αλλά αντίθετη φορά απεναντι απο . Το αντίθετο διάνυσμα συμβολίζεται με , για το αντίθετο διάνυσμα .

Στον αριθμό λειτουργίες γραμμής τα over vectors περιλαμβάνουν τις πράξεις της πρόσθεσης, της αφαίρεσης των διανυσμάτων και του πολλαπλασιασμού ενός διανύσματος με έναν αριθμό, δηλ. πράξεις που καταλήγουν σε ένα διάνυσμα.

Ας ορίσουμε αυτές τις πράξεις σε διανύσματα. Έστω δύο διανύσματα και δίνονται. Ας πάρουμε ένα αυθαίρετο σημείο Ο και ας κατασκευάσουμε ένα διάνυσμα , από το σημείο Α παραμερίζουμε το διάνυσμα . Τότε καλείται το διάνυσμα που συνδέει την αρχή του πρώτου όρου του διανύσματος με το τέλος του δεύτερου άθροισμα από αυτά τα διανύσματα και συμβολίζεται με . Ο θεωρούμενος κανόνας για την εύρεση του αθροίσματος των διανυσμάτων ονομάζεται κανόνες τριγώνου (Εικόνα 2.11).

Το ίδιο άθροισμα διανυσμάτων μπορεί να ληφθεί με άλλο τρόπο (Εικόνα 2.12). Αφήστε στην άκρη το διάνυσμα και το διάνυσμα από το σημείο. Ας χτίσουμε πάνω σε αυτά τα διανύσματα όπως στις πλευρές ενός παραλληλογράμμου. Το διάνυσμα , το οποίο είναι η διαγώνιος του παραλληλογράμμου που προέρχεται από την κορυφή , θα είναι το άθροισμα . Αυτός ο κανόνας για την εύρεση του αθροίσματος ονομάζεται κανόνες παραλληλογράμμου .

Το άθροισμα οποιουδήποτε πεπερασμένου αριθμού διανυσμάτων μπορεί να ληφθεί χρησιμοποιώντας τον κανόνα της διακεκομμένης γραμμής (Εικόνα 2.13). Από ένα αυθαίρετο σημείο, αναβάλλουμε το διάνυσμα , μετά αναβάλλουμε το διάνυσμα κ.λπ. Το διάνυσμα που συνδέει την αρχή του πρώτου με το τέλος του δεύτερου είναι το άθροισμα

διανύσματα δεδομένων, π.χ. . Προφανώς, αν το τέλος του τελευταίου όρου του διανύσματος συμπίπτει με την αρχή του πρώτου, τότε το άθροισμα των διανυσμάτων είναι ίσο με το μηδενικό διάνυσμα.

διαφορά δύο διανύσματα και λέγεται τέτοιο διάνυσμα , το άθροισμα του οποίου με το αφαιρούμενο διάνυσμα δίνει το διάνυσμα . Από εδώ Διανυσματικός κανόνας κατασκευής διαφοράς(Εικόνα 2.14). Από ένα σημείο παραμερίζουμε ένα διάνυσμα και ένα διάνυσμα . Το διάνυσμα που συνδέει τα άκρα του ανηγμένου διανύσματος και του διανύσματος που πρέπει να αφαιρεθεί και να κατευθυνθεί από το διάνυσμα που αφαιρείται στο ανηγμένο διάνυσμα είναι η διαφορά.

Διανυσματικό προϊόνσε πραγματικό αριθμό λ λέγεται ένα διάνυσμα που είναι συγγραμμικό με το διάνυσμα, έχει μήκος και ίδια φορά με το διάνυσμα αν και φορά αντίθετη από το διάνυσμα αν.

Εισήχθη γραμμικές πράξεις πάνω από διανύσματα έχουν ιδιότητες :

10 . Ανταλλαγή της πρόσθεσης: .

είκοσι . Συσχετισμός προσθήκης: .

τριάντα. Η ύπαρξη ουδέτερου στοιχείου με προσθήκη: .

40 . Η ύπαρξη του αντίθετου στοιχείου με πρόσθεση:

50 . Κατανομή του πολλαπλασιασμού με έναν αριθμό ως προς τη διανυσματική πρόσθεση: .

60 . Κατανομή πολλαπλασιασμού ενός διανύσματος με το άθροισμα δύο αριθμών:

70. Ιδιότητα συσχετισμού ως προς τον πολλαπλασιασμό ενός διανύσματος με ένα γινόμενο αριθμών: .

Ας δοθεί το σύστημα των διανυσμάτων:

Η παράσταση , όπου λ i (i = 1,2,…, n) είναι κάποιοι αριθμοί, ονομάζεται γραμμικός συνδυασμός συστήματα διανυσμάτων (2.1). Το σύστημα των διανυσμάτων (2.1) ονομάζεται γραμμικά εξαρτώμενος , αν ο γραμμικός συνδυασμός τους είναι ίσος με μηδέν, με την προϋπόθεση ότι δεν είναι ίσοι με μηδέν όλοι οι αριθμοί λ 1 , λ 2 , …, λ n. Το σύστημα των διανυσμάτων (2.1) ονομάζεται γραμμικά ανεξάρτητη , αν ο γραμμικός συνδυασμός τους είναι ίσος με μηδέν μόνο υπό την προϋπόθεση ότι όλοι οι αριθμοί λ i = 0 (). Είναι δυνατό να δοθεί ένας άλλος ορισμός της γραμμικής εξάρτησης των διανυσμάτων. Το σύστημα των διανυσμάτων (2.1) ονομάζεται γραμμικά εξαρτώμενος , εάν κάποιο διάνυσμα αυτού του συστήματος εκφράζεται γραμμικά ως προς τα υπόλοιπα, διαφορετικά το σύστημα των διανυσμάτων (2.1) γραμμικά ανεξάρτητη .

Για διανύσματα που βρίσκονται σε ένα επίπεδο, οι ακόλουθες προτάσεις είναι αληθείς.

10 . Οποιαδήποτε τρία διανύσματα στο επίπεδο εξαρτώνται γραμμικά.

είκοσι . Εάν ο αριθμός αυτών των διανυσμάτων στο επίπεδο είναι μεγαλύτερος από τρία, τότε εξαρτώνται επίσης γραμμικά.

τριάντα. Για να είναι γραμμικά ανεξάρτητα δύο διανύσματα στο επίπεδο, είναι απαραίτητο και αρκετό να είναι μη συγγραμμικά.

Έτσι, ο μέγιστος αριθμός γραμμικά ανεξάρτητων διανυσμάτων στο επίπεδο είναι δύο.

Τα διανύσματα ονομάζονται ομοεπίπεδη αν βρίσκονται στο ίδιο επίπεδο ή είναι παράλληλα στο ίδιο επίπεδο. Οι παρακάτω προτάσεις ισχύουν για διανύσματα χώρου.

10 . Οποιαδήποτε τέσσερα διανύσματα χώρου εξαρτώνται γραμμικά.

είκοσι . Εάν ο αριθμός των δεδομένων διανυσμάτων στο χώρο είναι μεγαλύτερος από τέσσερα, τότε είναι επίσης γραμμικά εξαρτώμενα.

τριάντα. Για να είναι τρία διανύσματα γραμμικά ανεξάρτητα, είναι απαραίτητο και αρκετό να είναι μη ομοεπίπεδα.

Έτσι, ο μέγιστος αριθμός γραμμικά ανεξάρτητων διανυσμάτων στο χώρο είναι τρία.

Οποιοδήποτε μέγιστο υποσύστημα γραμμικά ανεξάρτητων διανυσμάτων μέσω του οποίου εκφράζεται οποιοδήποτε διάνυσμα αυτού του συστήματος ονομάζεται βάση θεωρούνται διανυσματικά συστήματα . Είναι εύκολο να συμπεράνουμε ότι η βάση στο επίπεδο αποτελείται από δύο μη συγγραμμικά διανύσματα και η βάση στο χώρο αποτελείται από τρία μη ομοεπίπεδα διανύσματα. Ο αριθμός των διανυσμάτων βάσης ονομάζεται τάξη διανυσματικά συστήματα. Οι συντελεστές διαστολής ενός διανύσματος ως προς τα διανύσματα βάσης ονομάζονται διανυσματικές συντεταγμένες σε αυτή τη βάση.

Έστω τα διανύσματα να σχηματίσουν μια βάση και έστω , τότε οι αριθμοί λ 1 , λ 2 , λ 3 είναι οι συντεταγμένες του διανύσματος στη βάση. Σε αυτήν την περίπτωση, καταγράφουν. Μπορεί να φανεί ότι η επέκταση του διανύσματος σε όρους της βάσης είναι μοναδική. Η κύρια έννοια της βάσης είναι ότι οι γραμμικές πράξεις σε διανύσματα γίνονται συνηθισμένες γραμμικές πράξεις σε αριθμούς - οι συντεταγμένες αυτών των διανυσμάτων. Χρησιμοποιώντας τις ιδιότητες των γραμμικών πράξεων σε διανύσματα, μπορούμε να αποδείξουμε το ακόλουθο θεώρημα.

Θεώρημα. Όταν προστίθενται δύο διανύσματα, προστίθενται οι αντίστοιχες συντεταγμένες τους. Όταν ένα διάνυσμα πολλαπλασιάζεται με έναν αριθμό, όλες οι συντεταγμένες του πολλαπλασιάζονται με αυτόν τον αριθμό.

Έτσι, αν και , τότε , πού , και πού , λ είναι κάποιος αριθμός.

Συνήθως, το σύνολο όλων των διανυσμάτων στο επίπεδο, ανάγεται σε μια κοινή αρχή, με τις εισαγόμενες γραμμικές πράξεις, συμβολίζεται με V 2 , και το σύνολο όλων των διανυσμάτων του χώρου, ανάγεται σε μια κοινή αρχή, συμβολίζεται με V 3 . Τα σύνολα V 2 και V 3 ονομάζονται χώρους γεωμετρικών διανυσμάτων.

Γωνία μεταξύ των διανυσμάτωνκαι καλείται η μικρότερη γωνία () με την οποία ένα από τα διανύσματα πρέπει να περιστραφεί μέχρι να συμπέσει με το δεύτερο αφού φέρουμε αυτά τα διανύσματα σε μια κοινή αρχή.

Προϊόν με κουκκίδεςδύο διανύσματα λέγεται αριθμός ίσος με το γινόμενο των μονάδων αυτών των διανυσμάτων με το συνημίτονο της μεταξύ τους γωνίας. Τελική γινόμενο των διανυσμάτων και δηλώνει , ή

Αν η γωνία μεταξύ των διανυσμάτων και είναι ίση, τότε

Από γεωμετρική άποψη, το κλιμακωτό γινόμενο των διανυσμάτων είναι ίσο με το γινόμενο του συντελεστή ενός διανύσματος και της προβολής ενός άλλου διανύσματος σε αυτό. Από την ισότητα (2.2) προκύπτει ότι

Από εδώ συνθήκη ορθογωνικότητας δύο διανυσμάτων: δύο διανύσματακαι είναι ορθογώνιες αν και μόνο αν το κλιμακωτό γινόμενο τους είναι ίσο με μηδέν, δηλ. .

Το γινόμενο κουκίδων των διανυσμάτων δεν είναι γραμμική πράξη γιατί καταλήγει σε έναν αριθμό, όχι σε διάνυσμα.

Ιδιότητες του βαθμωτού προϊόντος.

1º. - ανταλλαξιμότητα.

2º. - διανομή.

3º. – συσχετισμός σε σχέση με έναν αριθμητικό παράγοντα.

4º. - ιδιότητα βαθμωτού τετραγώνου.

Η ιδιότητα 4º υποδηλώνει τον ορισμό διανυσματικό μήκος :

Ας δοθεί μια βάση στον χώρο V 3 , όπου τα διανύσματα είναι μοναδιαία διανύσματα (λέγονται orts), η διεύθυνση καθενός από τα οποία συμπίπτει με τη θετική κατεύθυνση των αξόνων συντεταγμένων Ox, Oy, Oz ενός ορθογώνιου καρτεσιανού συστήματος συντεταγμένων .

Ας επεκτείνουμε το διάνυσμα χώρου V 3 σύμφωνα με αυτή τη βάση (Εικόνα 2.15):

Διανύσματα ονομάζονται συστατικά ενός διανύσματος κατά μήκος των αξόνων συντεταγμένων, ή συνιστωσών, ενός αριθμού a x , a y , a zείναι οι ορθογώνιες καρτεσιανές συντεταγμένες του διανύσματος ένα. Η κατεύθυνση του διανύσματος καθορίζεται από τις γωνίες α, β, γ που σχηματίζει με τις γραμμές συντεταγμένων. Το συνημίτονο αυτών των γωνιών ονομάζεται διανυσματικοί οδηγοί. Στη συνέχεια τα συνημίτονα κατεύθυνσης καθορίζονται από τους τύπους:

Είναι εύκολο να το δείξεις αυτό

Εκφράζουμε το βαθμωτό γινόμενο σε συντεταγμένη μορφή.

Αφήστε και . Πολλαπλασιάζοντας αυτά τα διανύσματα ως πολυώνυμα και θεωρώντας ότι παίρνουμε μια έκφραση για εύρεση τελεία γινόμενο σε μορφή συντεταγμένων:

εκείνοι. το κλιμακωτό γινόμενο δύο διανυσμάτων ισούται με το άθροισμα των ζευγαρωμένων γινομένων των συντεταγμένων με το ίδιο όνομα.

Από τις (2.6) και (2.4) ακολουθεί ο τύπος εύρεσης διανυσματικό μήκος :

Από τις (2.6) και (2.7) παίρνουμε έναν τύπο για τον προσδιορισμό γωνία μεταξύ των διανυσμάτων:

Ένα τριπλό διανυσμάτων ονομάζεται διατεταγμένο αν υποδεικνύεται ποιο από αυτά θεωρείται το πρώτο, ποιο το δεύτερο και ποιο το τρίτο.

Διέταξε τριάδα διανυσμάτων που ονομάζεται σωστά , εάν αφού τα φέρουμε σε κοινή αρχή από το τέλος του τρίτου διανύσματος, η συντομότερη στροφή από το πρώτο στο δεύτερο διάνυσμα είναι αριστερόστροφα. Διαφορετικά, ονομάζεται το τριπλό των διανυσμάτων αριστερά . Για παράδειγμα, στο σχήμα 2.15, τα διανύσματα , , σχηματίζουν τη δεξιά τριάδα διανυσμάτων και τα διανύσματα , , σχηματίζουν την αριστερή τριάδα διανυσμάτων.

Η έννοια των δεξιών και αριστερών συστημάτων συντεταγμένων στον τρισδιάστατο χώρο εισάγεται με παρόμοιο τρόπο.

διανυσματική τέχνηδιάνυσμα σε διάνυσμα ονομάζεται διάνυσμα (άλλος συμβολισμός) που:

1) έχει μήκος , όπου είναι η γωνία μεταξύ των διανυσμάτων και ;

2) είναι κάθετο στα διανύσματα και (), δηλ. κάθετη στο επίπεδο που περιέχει τα διανύσματα και ;

Εξ ορισμού, βρίσκουμε το διανυσματικό γινόμενο των orts συντεταγμένων , , :

Αν , , τότε οι συντεταγμένες του διασταυρούμενου γινομένου ενός διανύσματος και ενός διανύσματος καθορίζονται από τον τύπο:

Από τον ορισμό προκύπτει γεωμετρική σημασία του διανυσματικού προϊόντος : ο συντελεστής του διανύσματος είναι ίσος με το εμβαδόν του παραλληλογράμμου που χτίζεται στα διανύσματα και .

Διανυσματικές ιδιότητες προϊόντος:

40 . , εάν τα διανύσματα και είναι συγγραμμικά, ή ένα από αυτά τα διανύσματα είναι μηδέν.

Παράδειγμα 3Το παραλληλόγραμμο είναι χτισμένο στα διανύσματα και , όπου , , . Υπολογίστε το μήκος των διαγωνίων αυτού του παραλληλογράμμου, τη γωνία μεταξύ των διαγωνίων και το εμβαδόν του παραλληλογράμμου.

Λύση.Η κατασκευή των διανυσμάτων και φαίνεται στο Σχήμα 2.16, η κατασκευή ενός παραλληλογράμμου σε αυτά τα διανύσματα φαίνεται στο Σχήμα 2.17.

Ας κάνουμε μια αναλυτική λύση αυτού του προβλήματος. Εκφράζουμε τα διανύσματα που ορίζουν τις διαγώνιους του κατασκευασμένου παραλληλογράμμου μέσω των διανυσμάτων και , και μετά μέσω και . Βρίσκουμε , . Στη συνέχεια, βρίσκουμε τα μήκη των διαγωνίων του παραλληλογράμμου, ως τα μήκη των κατασκευασμένων διανυσμάτων

Η γωνία μεταξύ των διαγωνίων του παραλληλογράμμου συμβολίζεται με . Τότε από τον τύπο για το βαθμωτό γινόμενο των διανυσμάτων έχουμε:

Ως εκ τούτου, .

Χρησιμοποιώντας τις ιδιότητες του διασταυρούμενου προϊόντος, υπολογίζουμε το εμβαδόν του παραλληλογράμμου:

Έστω τρία διανύσματα και . Φανταστείτε ότι ένα διάνυσμα πολλαπλασιάζεται διανυσματικά με και ένα διάνυσμα και το διάνυσμα που προκύπτει πολλαπλασιάζεται κλιμακωτικά με ένα διάνυσμα, καθορίζοντας έτσι τον αριθμό. Ονομάζεται διανυσματικός-κλιμακωτός ή ανάμεικτο προϊόν τρία διανύσματα και . Συμβολίζεται ή .

Ας ανακαλύψουμε γεωμετρική σημασία του μικτού προϊόντος (Εικόνα 2.18). Αφήστε το , , να μην είναι ομοεπίπεδο. Ας κατασκευάσουμε ένα παραλληλεπίπεδο σε αυτά τα διανύσματα όπως στις ακμές. Το εγκάρσιο γινόμενο είναι ένα διάνυσμα του οποίου το μέτρο είναι ίσο με το εμβαδόν του παραλληλογράμμου (η βάση του παραλληλεπίπεδου) που είναι χτισμένο πάνω στα διανύσματα και κατευθύνεται κάθετα στο επίπεδο του παραλληλογράμμου.

Τελική γινόμενο (ίσο με το γινόμενο του συντελεστή του διανύσματος και της προβολής στο ). Το ύψος του κατασκευασμένου παραλληλεπίπεδου είναι η απόλυτη τιμή αυτής της προβολής. Επομένως, η απόλυτη τιμή του μικτού γινόμενου τριών διανυσμάτων είναι ίση με τον όγκο του παραλληλεπίπεδου που χτίζεται στα διανύσματα και, δηλ. .

Εξ ου και ο όγκος της τριγωνικής πυραμίδας που είναι χτισμένη στα διανύσματα , και , υπολογίζεται από τον τύπο .

Σημειώνουμε μερικά ακόμη μικτές ιδιότητες του προϊόντος φορείς.

1 ο. Το πρόσημο του γινομένου είναι θετικό αν τα διανύσματα , , σχηματίζουν ένα σύστημα με το ίδιο όνομα με το κύριο, και αρνητικό διαφορετικά.

Πραγματικά, το γινόμενο με τελείες είναι θετικό εάν η γωνία μεταξύ και είναι οξεία και αρνητικό εάν η γωνία είναι αμβλεία. Με οξεία γωνία μεταξύ και, τα διανύσματα και βρίσκονται στην ίδια πλευρά σε σχέση με τη βάση του παραλληλεπίπεδου, και επομένως, από το τέλος του διανύσματος, η περιστροφή από το προς θα φαίνεται με τον ίδιο τρόπο όπως από το τέλος του το διάνυσμα, δηλ προς τη θετική κατεύθυνση (αριστερόστροφα).

Σε αμβλεία γωνία, και τα διανύσματα και βρίσκονται σε διαφορετικές πλευρές σε σχέση με το επίπεδο του παραλληλογράμμου που βρίσκεται στη βάση του παραλληλεπίπεδου, και επομένως, από το τέλος του διανύσματος, η περιστροφή από έως είναι ορατή προς την αρνητική κατεύθυνση ( δεξιόστροφος).

2 o Το μικτό προϊόν δεν μεταβάλλεται με κυκλική μετάθεση των παραγόντων του: .

3 o Όταν ανταλλάσσονται οποιαδήποτε δύο διανύσματα, το μικτό γινόμενο αλλάζει μόνο το πρόσημο. Για παράδειγμα, , . , . - άγνωστα συστήματα.

Σύστημα(3.1) καλείται ομοιογενής αν όλα τα ελεύθερα μέλη είναι . Σύστημα (3.1) καλείται ετερογενής , εάν τουλάχιστον ένα από τα ελεύθερα μέλη του .

Λύση συστήματοςονομάζεται σύνολο αριθμών, όταν αντικαθιστούμε στις εξισώσεις του συστήματος αντί των αντίστοιχων αγνώστων, κάθε εξίσωση του συστήματος μετατρέπεται σε ταυτότητα. Ένα σύστημα που δεν έχει λύση ονομάζεται ασύμβατες, ή αμφιλεγόμενος . Ένα σύστημα που έχει τουλάχιστον μία λύση ονομάζεται άρθρωση .

Το σύστημα άρθρωσης ονομάζεται βέβαιος αν έχει μοναδική λύση. Εάν ένα σύστημα άρθρωσης έχει περισσότερες από μία λύσεις, τότε καλείται αβέβαιος . Ένα ομοιογενές σύστημα είναι πάντα συνεπές, αφού έχει τουλάχιστον τη μηδενική λύση. Η έκφραση για τα άγνωστα, από τα οποία μπορεί να ληφθεί οποιαδήποτε συγκεκριμένη λύση του συστήματος, ονομάζεται κοινή λύση , και κάθε συγκεκριμένη λύση του συστήματος είναι δική του ιδιωτική απόφαση . Δύο συστήματα με τα ίδια άγνωστα είναι ισοδύναμα (ισοδυναμούν με ) εάν κάθε λύση ενός από αυτά είναι λύση του άλλου ή και τα δύο συστήματα είναι ασυνεπή.

Εξετάστε μεθόδους για την επίλυση συστημάτων γραμμικών εξισώσεων.

Μία από τις κύριες μεθόδους για την επίλυση συστημάτων γραμμικών εξισώσεων είναι μέθοδος Gauss, ή διαδοχική μέθοδος αποκλεισμός αγνώστων. Η ουσία αυτής της μεθόδου είναι να μειωθεί το σύστημα γραμμικών εξισώσεων σε μια σταδιακή μορφή. Σε αυτή την περίπτωση, οι εξισώσεις πρέπει να εκτελούν τα ακόλουθα στοιχειώδεις μεταμορφώσεις :

1. Μετάθεση των εξισώσεων του συστήματος.

2. Προσθήκη άλλης εξίσωσης σε μία εξίσωση.

3. Πολλαπλασιάζοντας και τις δύο πλευρές της εξίσωσης με έναν μη μηδενικό αριθμό.

Ως αποτέλεσμα, το σύστημα θα λάβει τη μορφή:

Συνεχίζοντας αυτή τη διαδικασία περαιτέρω, εξαλείφουμε το άγνωστο από όλες τις εξισώσεις, ξεκινώντας από την τρίτη. Για να γίνει αυτό, πολλαπλασιάζουμε τη δεύτερη εξίσωση με αριθμούς και προσθέτουμε στην 3η, ..., στην -η εξίσωση του συστήματος. Τα επόμενα βήματα της μεθόδου Gauss πραγματοποιούνται με παρόμοιο τρόπο. Εάν ως αποτέλεσμα των μετασχηματισμών προκύψει μια πανομοιότυπη εξίσωση, τότε τη διαγράφουμε από το σύστημα. Εάν σε κάποιο βήμα της μεθόδου Gauss προκύπτει μια εξίσωση της μορφής:

τότε το υπό εξέταση σύστημα είναι ασυνεπές και η περαιτέρω επίλυσή του σταματά. Εάν η εξίσωση της μορφής (3.2) δεν εμφανίζεται κατά την εκτέλεση στοιχειωδών μετασχηματισμών, τότε σε όχι περισσότερα από - βήματα το σύστημα (3.1) θα μετατραπεί σε μια σταδιακή μορφή:

Για να αποκτήσετε μια συγκεκριμένη λύση του συστήματος, θα χρειαστεί στο (3.4) να αντιστοιχίσετε συγκεκριμένες τιμές στις ελεύθερες μεταβλητές.

Σημειώστε ότι εφόσον στη μέθοδο Gauss όλοι οι μετασχηματισμοί εκτελούνται στους συντελεστές άγνωστων εξισώσεων και ελεύθερων όρων, στην πράξη αυτή η μέθοδος εφαρμόζεται συνήθως σε έναν πίνακα που αποτελείται από συντελεστές αγνώστων και μια στήλη ελεύθερων όρων. Αυτός ο πίνακας ονομάζεται εκτεταμένος. Με τη βοήθεια στοιχειωδών μετασχηματισμών, αυτός ο πίνακας μειώνεται σε κλιμακωτή μορφή. Μετά από αυτό, το σύστημα αποκαθίσταται χρησιμοποιώντας τη μήτρα που λήφθηκε και όλες οι προηγούμενες εκτιμήσεις εφαρμόζονται σε αυτό.

Παράδειγμα 1Επίλυση συστήματος:

Λύση.Συνθέτουμε τον επαυξημένο πίνακα και τον μειώνουμε σε μια κλιμακωτή μορφή:

~ *) ~ **) ~ ***)

*) - η δεύτερη γραμμή πολλαπλασιάζεται επί και η τρίτη γραμμή διαγράφεται.

Σε αυτό το άρθρο, θα εξετάσουμε τρόπους για τον προσδιορισμό της απόστασης από ένα σημείο σε ένα σημείο θεωρητικά και με το παράδειγμα συγκεκριμένων εργασιών. Ας ξεκινήσουμε με ορισμένους ορισμούς.

Ορισμός 1

Απόσταση μεταξύ σημείων- αυτό είναι το μήκος του τμήματος που τα συνδέει, στην υπάρχουσα κλίμακα. Είναι απαραίτητο να ρυθμίσετε την κλίμακα για να έχετε μια μονάδα μήκους για μέτρηση. Επομένως, βασικά το πρόβλημα της εύρεσης της απόστασης μεταξύ των σημείων επιλύεται χρησιμοποιώντας τις συντεταγμένες τους στη γραμμή συντεταγμένων, στο επίπεδο συντεταγμένων ή στον τρισδιάστατο χώρο.

Αρχικά δεδομένα: η ευθεία συντεταγμένων O x και ένα αυθαίρετο σημείο A που βρίσκεται πάνω της. Ένας πραγματικός αριθμός είναι εγγενής σε οποιοδήποτε σημείο της ευθείας: ας είναι ένας ορισμένος αριθμός για το σημείο Α xA,είναι η συντεταγμένη του σημείου Α.

Γενικά, μπορούμε να πούμε ότι η εκτίμηση του μήκους ενός συγκεκριμένου τμήματος γίνεται σε σύγκριση με το τμήμα που λαμβάνεται ως μονάδα μήκους σε μια δεδομένη κλίμακα.

Εάν το σημείο Α αντιστοιχεί σε έναν ακέραιο πραγματικό αριθμό, έχοντας παραμερίσει διαδοχικά από το σημείο Ο σε ένα σημείο κατά μήκος μιας ευθείας γραμμής τμήματα O A - μονάδες μήκους, μπορούμε να προσδιορίσουμε το μήκος του τμήματος Ο Α από τον συνολικό αριθμό των μεμονωμένων τμημάτων που εκκρεμούν.

Για παράδειγμα, το σημείο Α αντιστοιχεί στον αριθμό 3 - για να φτάσετε σε αυτό από το σημείο Ο, θα χρειαστεί να παραμερίσετε τρία τμήματα μονάδας. Αν το σημείο Α έχει συντεταγμένη -4, τα μεμονωμένα τμήματα σχεδιάζονται με παρόμοιο τρόπο, αλλά σε διαφορετική, αρνητική κατεύθυνση. Έτσι, στην πρώτη περίπτωση, η απόσταση O A είναι 3. στη δεύτερη περίπτωση, O A \u003d 4.

Εάν το σημείο Α έχει έναν ρητό αριθμό ως συντεταγμένη, τότε από την αρχή (σημείο Ο) παραμερίζουμε έναν ακέραιο αριθμό μονάδων τμημάτων και μετά το απαραίτητο μέρος του. Αλλά γεωμετρικά δεν είναι πάντα δυνατό να γίνει μια μέτρηση. Για παράδειγμα, φαίνεται δύσκολο να αφήσουμε στην άκρη το άμεσο κλάσμα συντεταγμένων 4 111 .

Με τον παραπάνω τρόπο, είναι εντελώς αδύνατο να αναβληθεί ένας παράλογος αριθμός σε ευθεία γραμμή. Για παράδειγμα, όταν η συντεταγμένη του σημείου Α είναι 11 . Σε αυτήν την περίπτωση, είναι δυνατό να στραφούμε στην αφαίρεση: εάν η δεδομένη συντεταγμένη του σημείου Α είναι μεγαλύτερη από το μηδέν, τότε O A \u003d x A (ο αριθμός λαμβάνεται ως απόσταση). αν η συντεταγμένη είναι μικρότερη από το μηδέν, τότε O A = - x A . Γενικά, αυτές οι προτάσεις ισχύουν για οποιονδήποτε πραγματικό αριθμό x A .

Συνοψίζοντας: η απόσταση από την αρχή έως το σημείο, που αντιστοιχεί σε έναν πραγματικό αριθμό στη γραμμή συντεταγμένων, είναι ίση με:

• 0 αν το σημείο είναι ίδιο με την προέλευση.

• x A εάν x A > 0 ;

• - x A εάν x A< 0 .

Στην περίπτωση αυτή, είναι προφανές ότι το μήκος του ίδιου του τμήματος δεν μπορεί να είναι αρνητικό, επομένως, χρησιμοποιώντας το πρόσημο του συντελεστή, γράφουμε την απόσταση από το σημείο Ο έως το σημείο Α με τη συντεταγμένη x Α: O A = x A

Η σωστή δήλωση θα ήταν: η απόσταση από το ένα σημείο στο άλλο θα είναι ίση με το μέτρο της διαφοράς των συντεταγμένων.Εκείνοι. για τα σημεία Α και Β που βρίσκονται στην ίδια γραμμή συντεταγμένων σε οποιαδήποτε θέση και έχουν, αντίστοιχα, τις συντεταγμένες x Ακαι x B: A B = x B - x A .

Αρχικά δεδομένα: τα σημεία A και B που βρίσκονται σε ένα επίπεδο σε ένα ορθογώνιο σύστημα συντεταγμένων O x y με δεδομένες συντεταγμένες: A (x A , y A) και B (x B , y B) .

Ας σχεδιάσουμε κάθετες στους άξονες συντεταγμένων O x και O y μέσω των σημείων A και B και πάρουμε τα σημεία προβολής ως αποτέλεσμα: A x , A y , B x , B y . Με βάση τη θέση των σημείων Α και Β, είναι περαιτέρω δυνατές οι ακόλουθες επιλογές:

Εάν τα σημεία Α και Β συμπίπτουν, τότε η απόσταση μεταξύ τους είναι μηδέν.

Εάν τα σημεία Α και Β βρίσκονται σε ευθεία γραμμή κάθετη στον άξονα Ο x (άξονας τετμημένης), τότε τα σημεία και συμπίπτουν και | Α Β | = | A y B y | . Εφόσον η απόσταση μεταξύ των σημείων είναι ίση με το μέτρο της διαφοράς μεταξύ των συντεταγμένων τους, τότε A y B y = y B - y A , και, επομένως, A B = A y B y = y B - y A .

Εάν τα σημεία Α και Β βρίσκονται σε ευθεία γραμμή κάθετη στον άξονα O y (άξονας y) - κατ' αναλογία με την προηγούμενη παράγραφο: A B = A x B x = x B - x A

Εάν τα σημεία Α και Β δεν βρίσκονται σε ευθεία γραμμή κάθετη σε έναν από τους άξονες συντεταγμένων, βρίσκουμε την απόσταση μεταξύ τους εξάγοντας τον τύπο υπολογισμού:

Βλέπουμε ότι το τρίγωνο A B C είναι ορθογώνιο κατά κατασκευή. Στην περίπτωση αυτή, A C = A x B x και B C = A y B y . Χρησιμοποιώντας το Πυθαγόρειο θεώρημα, συνθέτουμε την ισότητα: AB 2 = AC 2 + BC 2 ⇔ AB 2 = A x B x 2 + A y B y 2 , και στη συνέχεια τη μετατρέπουμε: AB = A x B x 2 + A y B y 2 = x B - x A 2 + y B - y A 2 = (x B - x A) 2 + (y B - y A) 2

Ας σχηματίσουμε ένα συμπέρασμα από το αποτέλεσμα που προέκυψε: η απόσταση από το σημείο Α στο σημείο Β στο επίπεδο καθορίζεται από τον υπολογισμό με τον τύπο που χρησιμοποιεί τις συντεταγμένες αυτών των σημείων

A B = (x B - x A) 2 + (y B - y A) 2

Ο προκύπτων τύπος επιβεβαιώνει επίσης τις δηλώσεις που σχηματίστηκαν προηγουμένως για τις περιπτώσεις σύμπτωσης σημείων ή καταστάσεων όπου τα σημεία βρίσκονται σε ευθείες γραμμές κάθετες στους άξονες. Άρα, για την περίπτωση της σύμπτωσης των σημείων Α και Β, η ισότητα θα ισχύει: A B = (x B - x A) 2 + (y B - y A) 2 = 0 2 + 0 2 = 0

Για την περίπτωση που τα σημεία Α και Β βρίσκονται σε ευθεία γραμμή κάθετη στον άξονα x:

A B = (x B - x A) 2 + (y B - y A) 2 = 0 2 + (y B - y A) 2 = y B - y A

Για την περίπτωση που τα σημεία Α και Β βρίσκονται σε ευθεία γραμμή κάθετη στον άξονα y:

A B = (x B - x A) 2 + (y B - y A) 2 = (x B - x A) 2 + 0 2 = x B - x A

Αρχικά δεδομένα: ορθογώνιο σύστημα συντεταγμένων O x y z με αυθαίρετα σημεία που βρίσκονται πάνω του με δεδομένες συντεταγμένες A (x A , y A , z A) και B (x B , y B , z B) . Είναι απαραίτητο να προσδιοριστεί η απόσταση μεταξύ αυτών των σημείων.

Εξετάστε τη γενική περίπτωση όταν τα σημεία Α και Β δεν βρίσκονται σε επίπεδο παράλληλο προς ένα από τα επίπεδα συντεταγμένων. Σχεδιάστε τα σημεία Α και Β επίπεδα κάθετα στους άξονες συντεταγμένων και λάβετε τα αντίστοιχα σημεία προβολής: A x , A y , A z , B x , B y , B z

Η απόσταση μεταξύ των σημείων Α και Β είναι η διαγώνιος του πλαισίου που προκύπτει. Σύμφωνα με την κατασκευή της μέτρησης αυτού του πλαισίου: A x B x , A y B y και A z B z

Από την πορεία της γεωμετρίας είναι γνωστό ότι το τετράγωνο της διαγωνίου ενός παραλληλεπίπεδου είναι ίσο με το άθροισμα των τετραγώνων των διαστάσεων του. Με βάση αυτή τη δήλωση, λαμβάνουμε την ισότητα: A B 2 \u003d A x B x 2 + A y B y 2 + A z B z 2

Χρησιμοποιώντας τα συμπεράσματα που προέκυψαν, γράφουμε τα εξής:

A x B x = x B - x A , A y B y = y B - y A , A z B z = z B - z A

Ας μετατρέψουμε την έκφραση:

AB 2 = A x B x 2 + A y B y 2 + A z B z 2 = x B - x A 2 + y B - y A 2 + z B - z A 2 = = (x B - x A) 2 + (y B - y A) 2 + z B - z A 2

Τελικός τύπος για τον προσδιορισμό της απόστασης μεταξύ σημείων στο χώροθα μοιάζει με αυτό:

A B = x B - x A 2 + y B - y A 2 + (z B - z A) 2

Ο τύπος που προκύπτει ισχύει επίσης για περιπτώσεις όπου:

Οι τελείες ταιριάζουν.

Βρίσκονται στον ίδιο άξονα συντεταγμένων ή σε ευθεία γραμμή παράλληλη με έναν από τους άξονες συντεταγμένων.

Παραδείγματα επίλυσης προβλημάτων για την εύρεση της απόστασης μεταξύ σημείων

Παράδειγμα 1

Αρχικά δεδομένα: δίνονται μια γραμμή συντεταγμένων και σημεία που βρίσκονται σε αυτήν με δεδομένες συντεταγμένες A (1 - 2) και B (11 + 2). Είναι απαραίτητο να βρεθεί η απόσταση από το σημείο αναφοράς Ο έως το σημείο Α και μεταξύ των σημείων Α και Β.

Λύση

1. Η απόσταση από το σημείο αναφοράς στο σημείο είναι ίση με τη μονάδα της συντεταγμένης αυτού του σημείου, αντίστοιχα O A \u003d 1 - 2 \u003d 2 - 1
2. Η απόσταση μεταξύ των σημείων Α και Β ορίζεται ως ο συντελεστής της διαφοράς μεταξύ των συντεταγμένων αυτών των σημείων: A B = 11 + 2 - (1 - 2) = 10 + 2 2

Απάντηση: O A = 2 - 1, A B = 10 + 2 2

Παράδειγμα 2

Αρχικά δεδομένα: δίνεται ένα ορθογώνιο σύστημα συντεταγμένων και δύο σημεία που βρίσκονται πάνω του A (1 , - 1) και B (λ + 1 , 3). Το λ είναι κάποιος πραγματικός αριθμός. Είναι απαραίτητο να βρεθούν όλες οι τιμές αυτού του αριθμού για τις οποίες η απόσταση A B θα είναι ίση με 5.

Λύση

Για να βρείτε την απόσταση μεταξύ των σημείων Α και Β, πρέπει να χρησιμοποιήσετε τον τύπο A B = (x B - x A) 2 + y B - y A 2

Αντικαθιστώντας τις πραγματικές τιμές των συντεταγμένων, παίρνουμε: A B = (λ + 1 - 1) 2 + (3 - (- 1)) 2 = λ 2 + 16

Και επίσης χρησιμοποιούμε την υπάρχουσα συνθήκη ότι A B = 5 και τότε η ισότητα θα είναι αληθής:

λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3

Απάντηση: A B \u003d 5 αν λ \u003d ± 3.

Παράδειγμα 3

Αρχικά δεδομένα: ένας τρισδιάστατος χώρος σε ένα ορθογώνιο σύστημα συντεταγμένων O x y z και δίνονται τα σημεία A (1 , 2 , 3) ​​και B - 7 , - 2 , 4 που βρίσκονται σε αυτό.

Λύση

Για να λύσουμε το πρόβλημα, χρησιμοποιούμε τον τύπο A B = x B - x A 2 + y B - y A 2 + (z B - z A) 2

Αντικαθιστώντας τις πραγματικές τιμές, παίρνουμε: A B = (- 7 - 1) 2 + (- 2 - 2) 2 + (4 - 3) 2 = 81 = 9

Απάντηση: | Α Β | = 9

Εάν παρατηρήσετε κάποιο λάθος στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter

Η επίλυση προβλημάτων στα μαθηματικά για τους μαθητές συνοδεύεται συχνά από πολλές δυσκολίες. Το να βοηθήσουμε τον μαθητή να αντιμετωπίσει αυτές τις δυσκολίες, καθώς και να τον διδάξουμε πώς να εφαρμόζει τις θεωρητικές του γνώσεις στην επίλυση συγκεκριμένων προβλημάτων σε όλες τις ενότητες του μαθήματος του μαθήματος "Μαθηματικά" είναι ο κύριος σκοπός του ιστότοπού μας.

Ξεκινώντας να λύνουν προβλήματα σχετικά με το θέμα, οι μαθητές θα πρέπει να είναι σε θέση να χτίσουν ένα σημείο σε ένα επίπεδο σύμφωνα με τις συντεταγμένες του, καθώς και να βρουν τις συντεταγμένες ενός δεδομένου σημείου.

Ο υπολογισμός της απόστασης μεταξύ δύο σημείων που λαμβάνονται στο επίπεδο A (x A, y A) και B (x B, y B) πραγματοποιείται με τον τύπο d \u003d √ ((x A - x B) 2 + (y A - y B) 2), όπου d είναι το μήκος του τμήματος που συνδέει αυτά τα σημεία στο επίπεδο.

Εάν ένα από τα άκρα του τμήματος συμπίπτει με την αρχή και το άλλο έχει συντεταγμένες M (x M; y M), τότε ο τύπος για τον υπολογισμό του d θα λάβει τη μορφή OM = √ (x M 2 + y M 2).

1. Υπολογισμός της απόστασης μεταξύ δύο σημείων με δεδομένες τις συντεταγμένες αυτών των σημείων

Παράδειγμα 1.

Βρείτε το μήκος του τμήματος που συνδέει τα σημεία A(2; -5) και B(-4; 3) στο επίπεδο συντεταγμένων (Εικ. 1).

Λύση.

Δίνεται η συνθήκη του προβλήματος: x A = 2; x B \u003d -4; y A = -5 και y B = 3. Να βρείτε το d.

Εφαρμόζοντας τον τύπο d \u003d √ ((x A - x B) 2 + (y A - y B) 2), παίρνουμε:

d \u003d AB \u003d √ ((2 - (-4)) 2 + (-5 - 3) 2) \u003d 10.

2. Υπολογισμός των συντεταγμένων ενός σημείου που ισαπέχει από τρία δεδομένα σημεία

Παράδειγμα 2

Να βρείτε τις συντεταγμένες του σημείου O 1, που απέχει από τα τρία σημεία A(7; -1) και B(-2; 2) και C(-1; -5).

Λύση.

Από τη διατύπωση της συνθήκης του προβλήματος προκύπτει ότι O 1 A \u003d O 1 B \u003d O 1 C. Έστω το επιθυμητό σημείο O 1 συντεταγμένες (a; b). Σύμφωνα με τον τύπο d \u003d √ ((x A - x B) 2 + (y A - y B) 2) βρίσκουμε:

O 1 A \u003d √ ((a - 7) 2 + (b + 1) 2);

O 1 V \u003d √ ((a + 2) 2 + (b - 2) 2);

O 1 C \u003d √ ((a + 1) 2 + (b + 5) 2).

Συνθέτουμε ένα σύστημα δύο εξισώσεων:

(√((a - 7) 2 + (b + 1) 2) = √((a + 2) 2 + (b - 2) 2),
(√((a - 7) 2 + (b + 1) 2) = √((a + 1) 2 + (b + 5) 2).

Αφού τετραγωνίσουμε την αριστερή και τη δεξιά πλευρά των εξισώσεων, γράφουμε:

((a - 7) 2 + (b + 1) 2 \u003d (a + 2) 2 + (b - 2) 2,
((a - 7) 2 + (b + 1) 2 = (a + 1) 2 + (b + 5) 2 .

Απλοποιώντας, γράφουμε

(-3a + b + 7 = 0,
(-2a - b + 3 = 0.

Έχοντας λύσει το σύστημα, παίρνουμε: a = 2; b = -1.

Το σημείο O 1 (2; -1) απέχει από τα τρία σημεία που δίνονται στην συνθήκη που δεν βρίσκονται σε μία ευθεία γραμμή. Αυτό το σημείο είναι το κέντρο ενός κύκλου που διέρχεται από τρία δεδομένα σημεία. (Εικ. 2).

3. Υπολογισμός της τετμημένης (τεταγμένης) σημείου που βρίσκεται στον άξονα της τετμημένης (τεταγμένης) και βρίσκεται σε δεδομένη απόσταση από αυτό το σημείο

Παράδειγμα 3

Η απόσταση από το σημείο Β(-5; 6) έως το σημείο Α που βρίσκεται στον άξονα x είναι 10. Βρείτε το σημείο Α.

Λύση.

Από τη διατύπωση της συνθήκης του προβλήματος προκύπτει ότι η τεταγμένη του σημείου Α είναι μηδέν και ΑΒ = 10.

Δηλώνοντας την τετμημένη του σημείου Α έως α, γράφουμε Α(α; 0).

AB \u003d √ ((a + 5) 2 + (0 - 6) 2) \u003d √ ((a + 5) 2 + 36).

Παίρνουμε την εξίσωση √((a + 5) 2 + 36) = 10. Απλοποιώντας την, έχουμε

a 2 + 10a - 39 = 0.

Οι ρίζες αυτής της εξίσωσης a 1 = -13; και 2 = 3.

Παίρνουμε δύο βαθμούς A 1 (-13; 0) και A 2 (3; 0).

Εξέταση:

A 1 B \u003d √ ((-13 + 5) 2 + (0 - 6) 2) \u003d 10.

A 2 B \u003d √ ((3 + 5) 2 + (0 - 6) 2) \u003d 10.

Και οι δύο βαθμοί που αποκτήθηκαν ταιριάζουν στην κατάσταση του προβλήματος (Εικ. 3).

4. Υπολογισμός της τετμημένης (τεταγμένης) σημείου που βρίσκεται στον άξονα της τετμημένης (τεταγμένης) και βρίσκεται στην ίδια απόσταση από δύο δεδομένα σημεία

Παράδειγμα 4

Βρείτε ένα σημείο στον άξονα Oy που βρίσκεται στην ίδια απόσταση από τα σημεία A (6; 12) και B (-8; 10).

Λύση.

Έστω οι συντεταγμένες του σημείου που απαιτείται από τη συνθήκη του προβλήματος, που βρίσκεται στον άξονα Oy, O 1 (0; β) (στο σημείο που βρίσκεται στον άξονα Oy, η τετμημένη είναι ίση με μηδέν). Από την προϋπόθεση ότι O 1 A \u003d O 1 B.

Σύμφωνα με τον τύπο d \u003d √ ((x A - x B) 2 + (y A - y B) 2) βρίσκουμε:

O 1 A \u003d √ ((0 - 6) 2 + (b - 12) 2) \u003d √ (36 + (b - 12) 2);

O 1 V \u003d √ ((a + 8) 2 + (b - 10) 2) \u003d √ (64 + (b - 10) 2).

Έχουμε την εξίσωση √(36 + (b - 12) 2) = √(64 + (b - 10) 2) ή 36 + (b - 12) 2 = 64 + (b - 10) 2 .

Μετά την απλοποίηση, παίρνουμε: b - 4 = 0, b = 4.

Απαιτείται από τη συνθήκη του προβλήματος σημείο O 1 (0; 4) (Εικ. 4).

5. Υπολογισμός των συντεταγμένων ενός σημείου που βρίσκεται στην ίδια απόσταση από τους άξονες συντεταγμένων και κάποιο δεδομένο σημείο

Παράδειγμα 5

Βρείτε το σημείο Μ που βρίσκεται στο επίπεδο συντεταγμένων στην ίδια απόσταση από τους άξονες συντεταγμένων και από το σημείο Α (-2; 1).

Λύση.

Το απαιτούμενο σημείο M, όπως το σημείο A (-2, 1), βρίσκεται στη δεύτερη γωνία συντεταγμένων, καθώς απέχει από τα σημεία A, P 1 και P 2 (Εικ. 5). Οι αποστάσεις του σημείου Μ από τους άξονες των συντεταγμένων είναι ίδιες, επομένως, οι συντεταγμένες του θα είναι (-a; a), όπου a > 0.

Από τις συνθήκες του προβλήματος προκύπτει ότι MA = MP 1 = MP 2, MP 1 = a; MP 2 = |-a|,

εκείνοι. |-α| = α.

Σύμφωνα με τον τύπο d \u003d √ ((x A - x B) 2 + (y A - y B) 2) βρίσκουμε:

MA \u003d √ ((-a + 2) 2 + (a - 1) 2).

Ας κάνουμε μια εξίσωση:

√ ((-a + 2) 2 + (a - 1) 2) = a.

Μετά τον τετραγωνισμό και την απλοποίηση, έχουμε: a 2 - 6a + 5 = 0. Λύνουμε την εξίσωση, βρίσκουμε a 1 = 1; και 2 = 5.

Λαμβάνουμε δύο βαθμούς M 1 (-1; 1) και M 2 (-5; 5), ικανοποιώντας τη συνθήκη του προβλήματος.

6. Υπολογισμός των συντεταγμένων ενός σημείου που βρίσκεται στην ίδια καθορισμένη απόσταση από τον άξονα της τετμημένης (τεταγμένης) και από αυτό το σημείο

Παράδειγμα 6

Βρείτε ένα σημείο Μ τέτοιο ώστε η απόσταση του από τον άξονα y και από το σημείο Α (8, 6) να είναι ίση με 5.

Λύση.

Από την συνθήκη του προβλήματος προκύπτει ότι MA = 5 και η τετμημένη του σημείου M είναι ίση με 5. Έστω η τεταγμένη του σημείου M ίση με b, τότε M(5; b) (Εικ. 6).

Σύμφωνα με τον τύπο d \u003d √ ((x A - x B) 2 + (y A - y B) 2) έχουμε:

MA \u003d √ ((5 - 8) 2 + (b - 6) 2).

Ας κάνουμε μια εξίσωση:

√((5 - 8) 2 + (b - 6) 2) = 5. Απλοποιώντας το, παίρνουμε: b 2 - 12b + 20 = 0. Οι ρίζες αυτής της εξίσωσης είναι b 1 = 2; b 2 \u003d 10. Επομένως, υπάρχουν δύο σημεία που ικανοποιούν την προϋπόθεση του προβλήματος: M 1 (5; 2) και M 2 (5; 10).

Είναι γνωστό ότι πολλοί μαθητές, όταν λύνουν προβλήματα μόνοι τους, χρειάζονται συνεχείς διαβουλεύσεις για τεχνικές και μεθόδους επίλυσής τους. Συχνά, ένας μαθητής δεν μπορεί να βρει τρόπο να λύσει ένα πρόβλημα χωρίς τη βοήθεια ενός δασκάλου. Ο μαθητής μπορεί να λάβει τις απαραίτητες συμβουλές για την επίλυση προβλημάτων στην ιστοσελίδα μας.

Έχετε ερωτήσεις; Δεν είστε σίγουροι πώς να βρείτε την απόσταση μεταξύ δύο σημείων σε ένα επίπεδο;
Για να λάβετε τη βοήθεια ενός δασκάλου - εγγραφείτε.
Το πρώτο μάθημα είναι δωρεάν!

site, με πλήρη ή μερική αντιγραφή του υλικού, απαιτείται σύνδεσμος στην πηγή.