Η γεωμετρία ως ξεχωριστό μάθημα ξεκινά για τους μαθητές της 7ης τάξης. Μέχρι εκείνη την ώρα αγγίζουν γεωμετρικά προβλήματαμια αρκετά ελαφριά μορφή και βασικά αυτό που μπορεί να δει κανείς χρησιμοποιώντας οπτικά παραδείγματα: η περιοχή ενός δωματίου, ένα οικόπεδο, το μήκος και το ύψος των τοίχων σε δωμάτια, επίπεδα αντικείμενα κ.λπ. Στην αρχή της ίδιας της μελέτης της γεωμετρίας, εμφανίζονται οι πρώτες δυσκολίες, όπως, για παράδειγμα, η έννοια της ευθείας γραμμής, αφού δεν είναι δυνατό να αγγίξετε αυτήν την ευθεία γραμμή με τα χέρια σας. Όσο για τα τρίγωνα, αυτός είναι ο απλούστερος τύπος πολυγώνου, που περιέχει μόνο τρεις γωνίες και τρεις πλευρές.

Σε επαφή με

Συμμαθητές

Το θέμα των τριγώνων είναι ένα από τα κύρια σπουδαίοςκαι μεγάλα θέματα σχολικό πρόγραμμα σπουδώνστη γεωμετρία 7-9 τάξεις. Έχοντας κατακτήσει καλά, είναι δυνατό να αποφασίσετε πολύ σύνθετες εργασίες. Σε αυτή την περίπτωση, μπορείτε αρχικά να εξετάσετε ένα εντελώς διαφορετικό γεωμετρικό σχήμα και στη συνέχεια να το χωρίσετε για ευκολία σε κατάλληλα τριγωνικά μέρη.

Να δουλέψουμε για την απόδειξη της ισότητας ∆ ABCΚαι ∆A1B1C1Πρέπει να κατανοήσετε διεξοδικά τα σημάδια της ισότητας των μορφών και να είστε σε θέση να τα χρησιμοποιήσετε. Πριν μελετήσετε τα σημάδια, πρέπει να μάθετε καθορίζουν την ισότηταπλευρές και γωνίες των απλούστερων πολυγώνων.

Για να αποδείξετε ότι οι γωνίες των τριγώνων είναι ίσες, θα σας βοηθήσουν οι ακόλουθες επιλογές:

  1. ∠ α = ∠ β με βάση την κατασκευή των σχημάτων.
  2. Δίνεται στις συνθήκες εργασίας.
  3. Με δύο παράλληλες ευθείες και την παρουσία τομής μπορούν να σχηματιστούν εσωτερικές εγκάρσιες και αντίστοιχες ∠ α = ∠ β.
  4. Πρόσθεση (αφαίρεση) στο (από) ∠ α = ∠ β ίσες γωνίες.
  5. Τα κάθετα ∠ α και ∠ β είναι πάντα παρόμοια
  6. Γενική ∠ α, ταυτοχρόνως ανήκουσα σε ∆MNKΚαι ∆MNH .
  7. Η διχοτόμος χωρίζει το ∠ α σε δύο ίσα μέρη.
  8. Πλησίον ∠ 90°- γωνία ίση με την αρχική.
  9. Οι γειτονικές ίσες γωνίες είναι ίσες.
  10. Το ύψος σχηματίζει δύο γειτονικά ∠ 90° .
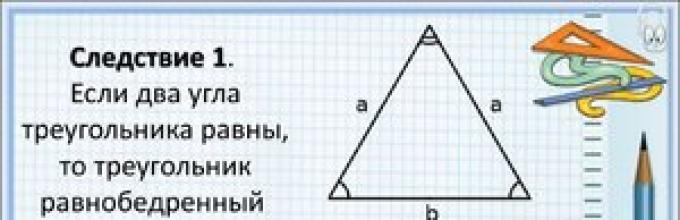
  11. Σε ισοσκελές ∆MNKστη βάση ∠ α = ∠ β.
  12. Ισος ∆MNKΚαι ∆SDHαντίστοιχο ∠ α = ∠ β.
  13. Προηγουμένως αποδεδειγμένη ισότητα ∆MNKΚαι ∆SDH .

Αυτό είναι ενδιαφέρον: Πώς να βρείτε την περίμετρο ενός τριγώνου.

3 σημάδια ότι τα τρίγωνα είναι ίσα

Απόδειξη ισότητας ∆ ABCΚαι ∆A1B1C1πολύ βολικό στην παραγωγή, με βάση το βασικό σημάδιατην ταυτότητα αυτών των απλούστερων πολυγώνων. Υπάρχουν τρία τέτοια σημάδια. Είναι πολύ σημαντικά για την επίλυση πολλών γεωμετρικών προβλημάτων. Κάθε ένα αξίζει να εξεταστεί.

Τα χαρακτηριστικά που αναφέρονται παραπάνω είναι θεωρήματα και αποδεικνύονται με τη μέθοδο της υπέρθεσης ενός σχήματος σε ένα άλλο, συνδέοντας κορυφές αντίστοιχες γωνίεςκαι η αρχή των ακτίνων. Οι αποδείξεις για την ισότητα των τριγώνων στην τάξη 7 περιγράφονται με πολύ προσιτή μορφή, αλλά είναι δύσκολο για τους μαθητές να μελετήσουν στην πράξη, καθώς περιέχουν ένας μεγάλος αριθμός απόστοιχεία που χαρακτηρίζονται με κεφαλαία λατινικά γράμματα. Αυτό δεν είναι απολύτως οικείο σε πολλούς μαθητές όταν αρχίζουν να μελετούν το θέμα. Οι έφηβοι μπερδεύονται σχετικά με τα ονόματα των πλευρών, των ακτίνων και των γωνιών.

Λίγο αργότερα εμφανίζεται ένα άλλο σημαντικό θέμα«Ομοιότητα τριγώνων». Ο ίδιος ο ορισμός της «ομοιότητας» στη γεωμετρία σημαίνει ομοιότητα σχήματοςμε διαφορετικά μεγέθη. Για παράδειγμα, μπορείτε να πάρετε δύο τετράγωνα, το πρώτο με πλευρά 4 εκ. και το δεύτερο 10 εκ. Αυτοί οι τύποι τετράγωνων θα είναι παρόμοιοι και, ταυτόχρονα, θα έχουν διαφορά, αφού το δεύτερο θα είναι μεγαλύτερο, με κάθε πλευρά αυξήθηκε κατά τον ίδιο αριθμό φορές.

Κατά την εξέταση του θέματος της ομοιότητας, δίνονται επίσης 3 σημάδια:

  • Το πρώτο αφορά τις δύο αντίστοιχα ίσες γωνίες των δύο τριγωνικών σχημάτων.
  • Το δεύτερο αφορά τη γωνία και τις πλευρές που τη σχηματίζουν ∆MNK, τα οποία είναι ίσα με τα αντίστοιχα στοιχεία ∆SDH .
  • Το τρίτο δείχνει την αναλογικότητα όλων των αντίστοιχων πλευρών των δύο επιθυμητών σχημάτων.

Πώς μπορείτε να αποδείξετε ότι τα τρίγωνα είναι παρόμοια; Αρκεί να χρησιμοποιήσετε ένα από τα παραπάνω σημάδια και να περιγράψετε σωστά ολόκληρη τη διαδικασία απόδειξης της εργασίας. Θέμα ομοιότητας ∆MNKΚαι ∆SDHείναι ευκολότερο να γίνει αντιληπτό από τους μαθητές με βάση το γεγονός ότι μέχρι τη στιγμή της μελέτης του, οι μαθητές χρησιμοποιούν ήδη ελεύθερα τους χαρακτηρισμούς των στοιχείων σε γεωμετρικές κατασκευές, δεν μπερδεύονται σε έναν τεράστιο αριθμό ονομάτων και ξέρουν πώς να διαβάζουν σχέδια.

Ολοκληρώνοντας το απόσπασμα του εκτενούς θέματος του τριγωνικού γεωμετρικά σχήματα, οι μαθητές θα πρέπει ήδη να γνωρίζουν τέλεια πώς να αποδεικνύουν την ισότητα ∆MNK = ∆SDHσε δύο πλευρές, ορίστε τα δύο τρίγωνα να είναι ίσα ή όχι. Λαμβάνοντας υπόψη ότι ένα πολύγωνο με ακριβώς τρεις γωνίες είναι ένα από τα πιο σημαντικά γεωμετρικά σχήματα, θα πρέπει να λάβετε σοβαρά υπόψη το υλικό, δίνοντας ιδιαίτερη προσοχή ακόμη και στα πιο μικρά δεδομένα της θεωρίας.

Δύο τρίγωνα λέγονται ίσα εάν μπορούν να ενωθούν με επικάλυψη. Το σχήμα 1 δείχνει ίσο τρίγωνα ABCκαι Α 1 Β 1 Γ 1 . Κάθε ένα από αυτά τα τρίγωνα μπορεί να τοποθετηθεί πάνω στο άλλο έτσι ώστε να είναι απολύτως συμβατά, δηλαδή οι κορυφές και οι πλευρές τους να είναι συμβατές σε ζεύγη. Είναι σαφές ότι οι γωνίες αυτών των τριγώνων θα ταιριάζουν επίσης σε ζεύγη.

Έτσι, εάν δύο τρίγωνα είναι ίσα, τότε τα στοιχεία (δηλαδή οι πλευρές και οι γωνίες) ενός τριγώνου είναι αντίστοιχα ίσα με τα στοιχεία του άλλου τριγώνου. Σημειώστε ότι σε ίσα τρίγωνα έναντι αντίστοιχα ίσων πλευρών(δηλαδή επικάλυψη όταν υπερτίθεται) ίσες γωνίες βρίσκονταικαι πίσω: Οι ίσες πλευρές βρίσκονται απέναντι, αντίστοιχα, ίσες γωνίες.

Έτσι, για παράδειγμα, σε ίσα τρίγωνα ABC και A 1 B 1 C 1, που φαίνονται στο σχήμα 1, απέναντι από τις ίσες πλευρές AB και A 1 B 1, αντίστοιχα, βρίσκονται ίσες γωνίες C και C 1. Θα συμβολίσουμε την ισότητα των τριγώνων ABC και A 1 B 1 C 1 ως εξής: Δ ABC = Δ A 1 B 1 C 1. Αποδεικνύεται ότι η ισότητα δύο τριγώνων μπορεί να διαπιστωθεί συγκρίνοντας ορισμένα από τα στοιχεία τους.

Θεώρημα 1. Το πρώτο σημάδι ισότητας τριγώνων.Εάν δύο πλευρές και η μεταξύ τους γωνία ενός τριγώνου είναι αντίστοιχα ίσες με δύο πλευρές και η μεταξύ τους γωνία ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα (Εικ. 2).

Απόδειξη. Θεωρήστε τα τρίγωνα ABC και A 1 B 1 C 1, στα οποία AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 (βλ. Εικ. 2). Ας αποδείξουμε ότι Δ ABC = Δ A 1 B 1 C 1 .

Εφόσον ∠ A = ∠ A 1, τότε το τρίγωνο ABC μπορεί να υπερτεθεί στο τρίγωνο A 1 B 1 C 1 έτσι ώστε η κορυφή A να ευθυγραμμίζεται με την κορυφή A 1 και οι πλευρές AB και AC να υπερτίθενται αντίστοιχα στις ακτίνες A 1 B 1 και A 1 Γ 1 . Εφόσον AB = A 1 B 1, AC = A 1 C 1, τότε η πλευρά AB θα ευθυγραμμιστεί με την πλευρά A 1 B 1 και η πλευρά AC θα ευθυγραμμιστεί με την πλευρά A 1 C 1. Ειδικότερα, τα σημεία Β και Β 1, Γ και Γ 1 θα συμπίπτουν. Κατά συνέπεια, οι πλευρές BC και B 1 C 1 θα ευθυγραμμιστούν. Έτσι, τα τρίγωνα ABC και A 1 B 1 C 1 είναι απολύτως συμβατά, που σημαίνει ότι είναι ίσα.

Το θεώρημα 2 αποδεικνύεται με παρόμοιο τρόπο χρησιμοποιώντας τη μέθοδο της υπέρθεσης.

Θεώρημα 2. Το δεύτερο σημάδι ισότητας τριγώνων.Εάν μια πλευρά και δύο γειτονικές γωνίες ενός τριγώνου είναι αντίστοιχα ίσες με την πλευρά και δύο γειτονικές γωνίες ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα (Εικ. 34).

Σχόλιο. Με βάση το Θεώρημα 2, καθιερώνεται το Θεώρημα 3.

Θεώρημα 3. Το άθροισμα οποιωνδήποτε δύο εσωτερικών γωνιών ενός τριγώνου είναι μικρότερο από 180°.

Το θεώρημα 4 προκύπτει από το τελευταίο θεώρημα.

Θεώρημα 4. Μια εξωτερική γωνία ενός τριγώνου είναι μεγαλύτερη από οποιαδήποτε εσωτερική γωνία που δεν γειτνιάζει με αυτό.

Θεώρημα 5. Το τρίτο σημάδι ισότητας τριγώνων.Εάν τρεις πλευρές ενός τριγώνου είναι αντίστοιχα ίσες με τρεις πλευρές ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα ().

Παράδειγμα 1.Στα τρίγωνα ABC και DEF (Εικ. 4)

∠ A = ∠ E, AB = 20 cm, AC = 18 cm, DE = 18 cm, EF = 20 εκ. Συγκρίνετε τρίγωνα ABC και DEF. Ποια γωνία στο τρίγωνο DEF είναι ίση με τη γωνία Β;

Λύση. Αυτά τα τρίγωνα είναι ίσα σύμφωνα με το πρώτο πρόσημο. Η γωνία F του τριγώνου DEF είναι ίση με τη γωνία Β του τριγώνου ABC, αφού αυτές οι γωνίες βρίσκονται απέναντι από ίσες πλευρές DE και AC αντίστοιχα.

Παράδειγμα 2.Τα τμήματα AB και CD (Εικ. 5) τέμνονται στο σημείο Ο, που είναι το μέσο καθενός από αυτά. Ποιο είναι το μήκος του τμήματος BD αν το τμήμα AC είναι 6 m;

Λύση. Τα τρίγωνα AOC και BOD είναι ίσα (σύμφωνα με το πρώτο κριτήριο): ∠ AOC = ∠ BOD (κάθετο), AO = OB, CO = OD (κατά συνθήκη).
Από την ισότητα αυτών των τριγώνων προκύπτει ότι οι πλευρές τους είναι ίσες, δηλαδή AC = BD. Επειδή όμως σύμφωνα με την συνθήκη AC = 6 m, τότε BD = 6 m.

Από την αρχαιότητα μέχρι σήμερα, η αναζήτηση σημείων ισότητας των μορφών θεωρείται βασικό έργο, που αποτελεί τη βάση των θεμελίων της γεωμετρίας. εκατοντάδες θεωρήματα αποδεικνύονται χρησιμοποιώντας τεστ ισότητας. Η ικανότητα απόδειξης της ισότητας και της ομοιότητας των μορφών είναι ένα σημαντικό έργο σε όλους τους τομείς της κατασκευής.

Σε επαφή με

Εφαρμογή της ικανότητας στην πράξη

Ας υποθέσουμε ότι έχουμε μια φιγούρα ζωγραφισμένη σε ένα κομμάτι χαρτί. Ταυτόχρονα, έχουμε έναν χάρακα και ένα μοιρογνωμόνιο με τα οποία μπορούμε να μετρήσουμε τα μήκη των τμημάτων και τις γωνίες μεταξύ τους. Πώς να μεταφέρετε μια φιγούρα ίδιου μεγέθους σε ένα δεύτερο φύλλο χαρτιού ή να διπλασιάσετε την κλίμακα του.

Γνωρίζουμε ότι ένα τρίγωνο είναι ένα σχήμα που αποτελείται από τρία τμήματα που ονομάζονται πλευρές που σχηματίζουν τις γωνίες. Έτσι, υπάρχουν έξι παράμετροι - τρεις πλευρές και τρεις γωνίες - που ορίζουν αυτό το σχήμα.

Ωστόσο, έχοντας μετρήσει το μέγεθος και των τριών πλευρών και γωνιών, η μεταφορά αυτού του αριθμού σε άλλη επιφάνεια θα είναι μια δύσκολη εργασία. Επιπλέον, είναι λογικό να τεθεί το ερώτημα: δεν θα ήταν αρκετό να γνωρίζουμε τις παραμέτρους δύο πλευρών και μιας γωνίας ή μόνο τριών πλευρών;

Έχοντας μετρήσει το μήκος των δύο πλευρών και μεταξύ τους, θα βάλουμε αυτή τη γωνία σε ένα νέο κομμάτι χαρτί, ώστε να μπορέσουμε να αναδημιουργήσουμε πλήρως το τρίγωνο. Ας μάθουμε πώς να το κάνουμε αυτό, ας μάθουμε πώς να αποδείξουμε τα σημάδια με τα οποία μπορούν να θεωρηθούν ίδια και να αποφασίσουμε ποιος ελάχιστος αριθμός παραμέτρων είναι αρκετός για να γνωρίζουμε για να είμαστε σίγουροι ότι τα τρίγωνα είναι τα ίδια.

Σπουδαίος!Τα σχήματα ονομάζονται πανομοιότυπα εάν τα τμήματα που σχηματίζουν τις πλευρές και τις γωνίες τους είναι ίσα μεταξύ τους. Παρόμοια σχήματα είναι εκείνα των οποίων οι πλευρές και οι γωνίες είναι ανάλογες. Έτσι, η ισότητα είναι ομοιότητα με συντελεστή αναλογικότητας 1.

Ποια είναι τα σημάδια της ισότητας των τριγώνων; Ας δώσουμε τον ορισμό τους:

  • το πρώτο σημάδι ισότητας: δύο τρίγωνα μπορούν να θεωρηθούν πανομοιότυπα αν δύο από τις πλευρές τους είναι ίσες, καθώς και η μεταξύ τους γωνία.
  • το δεύτερο σημάδι ισότητας τριγώνων: δύο τρίγωνα θα είναι ίδια αν δύο γωνίες είναι ίδιες, καθώς και η αντίστοιχη πλευρά μεταξύ τους.
  • τρίτο σημάδι ισότητας τριγώνων : Τα τρίγωνα μπορούν να θεωρηθούν πανομοιότυπα όταν όλες οι πλευρές τους έχουν ίσο μήκος.

Πώς να αποδείξετε ότι τα τρίγωνα είναι ίσα. Ας δώσουμε μια απόδειξη της ισότητας των τριγώνων.

Απόδειξη 1 σημείου

Για πολύ καιρό, μεταξύ των πρώτων μαθηματικών αυτό το ζώδιο θεωρούνταν αξίωμα, ωστόσο, όπως αποδείχθηκε, μπορεί να αποδειχθεί γεωμετρικά με βάση πιο βασικά αξιώματα.

Θεωρήστε δύο τρίγωνα - KMN και K 1 M 1 N 1 . Η πλευρά KM έχει το ίδιο μήκος με το K 1 M 1 και KN = K 1 N 1. Και η γωνία MKN είναι ίση με τις γωνίες KMN και M 1 K 1 N 1.

Αν θεωρήσουμε τις KM και K 1 M 1, KN και K 1 N 1 ως δύο ακτίνες που βγαίνουν από το ίδιο σημείο, τότε μπορούμε να πούμε ότι οι γωνίες μεταξύ αυτών των ζευγών ακτίνων είναι ίδιες (αυτό καθορίζεται από την συνθήκη το θεώρημα). Ας πραγματοποιήσουμε μια παράλληλη μεταφορά των ακτίνων K 1 M 1 και K 1 N 1 από το σημείο K 1 στο σημείο K. Ως αποτέλεσμα αυτής της μεταφοράς, οι ακτίνες K 1 M 1 και K 1 N 1 θα συμπέσουν πλήρως. Ας σχεδιάσουμε στην ακτίνα K 1 M 1 ένα τμήμα μήκους KM, που προέρχεται από το σημείο K. Εφόσον, κατά συνθήκη, το τμήμα που προκύπτει θα είναι ίσο με το τμήμα K 1 M 1, τότε τα σημεία M και M 1 συμπίπτουν. Ομοίως με τα τμήματα KN και K 1 N 1. Έτσι, μεταφέροντας K 1 M 1 N 1 έτσι ώστε τα σημεία K 1 και K να συμπίπτουν και οι δύο πλευρές να επικαλύπτονται, προκύπτει μια πλήρης σύμπτωση των ίδιων των σχημάτων.

Σπουδαίος!Στο Διαδίκτυο υπάρχουν αποδείξεις για την ισότητα των τριγώνων που βασίζονται σε δύο πλευρές και μια γωνία χρησιμοποιώντας αλγεβρικό και τριγωνομετρικές ταυτότητεςμε αριθμητικές τιμές πλευρών και γωνιών. Ωστόσο, ιστορικά και μαθηματικά αυτό το θεώρημαδιατυπώθηκε πολύ πριν από την άλγεβρα και πριν από την τριγωνομετρία. Για να αποδείξουμε αυτό το χαρακτηριστικό του θεωρήματος, είναι εσφαλμένο να χρησιμοποιούμε οτιδήποτε άλλο εκτός από τα βασικά αξιώματα.

Απόδειξη 2 σημάδια

Ας αποδείξουμε το δεύτερο πρόσημο της ισότητας σε δύο γωνίες και μια πλευρά, με βάση το πρώτο.

Απόδειξη 2 σημάδια

Ας εξετάσουμε το KMN και το PRS. Το K είναι ίσο με το P, το N είναι ίσο με το S. Η πλευρά KN έχει το ίδιο μήκος με το PS. Είναι απαραίτητο να αποδειχθεί ότι το KMN και το PRS είναι το ίδιο.

Ας αντικατοπτρίσουμε το σημείο M σε σχέση με την ακτίνα KN. Ας ονομάσουμε το σημείο που προκύπτει L. Σε αυτή την περίπτωση, το μήκος της πλευράς KM = KL. Το NKL είναι ίσο με το PRS. Το KNL είναι ίσο με RSP.

Εφόσον το άθροισμα των γωνιών είναι ίσο με 180 μοίρες, τότε το KLN είναι ίσο με το PRS, που σημαίνει ότι το PRS και το KLN είναι ίδια (παρόμοια) και στις δύο πλευρές και στη γωνία, σύμφωνα με το πρώτο πρόσημο.

Όμως, εφόσον το KNL είναι ίσο με το KMN, τότε το KMN και το PRS είναι δύο πανομοιότυπα ψηφία.

Απόδειξη 3 σημάδια

Πώς να προσδιορίσετε ότι τα τρίγωνα είναι ίσα. Αυτό προκύπτει άμεσα από την απόδειξη του δεύτερου χαρακτηριστικού.

Μήκος KN = PS. Εφόσον K = P, N = S, KL=KM και KN = KS, MN=ML, τότε:

Αυτό σημαίνει ότι και οι δύο φιγούρες είναι παρόμοιες μεταξύ τους. Επειδή όμως οι πλευρές τους είναι ίδιες, είναι και ίσες.

Πολλές συνέπειες προκύπτουν από τα σημάδια της ισότητας και της ομοιότητας. Ένα από αυτά είναι ότι για να προσδιοριστεί εάν δύο τρίγωνα είναι ίσα ή όχι, είναι απαραίτητο να γνωρίζουμε τις ιδιότητές τους, αν είναι ίδιες:

  • και οι τρεις πλευρές?
  • και οι δύο πλευρές και η γωνία μεταξύ τους.
  • και οι δύο γωνίες και η πλευρά μεταξύ τους.

Χρήση του τεστ ισότητας τριγώνου για την επίλυση προβλημάτων

Συνέπειες του πρώτου σημείου

Κατά τη διάρκεια της απόδειξης, μπορεί κανείς να καταλήξει σε μια σειρά από ενδιαφέρουσες και χρήσιμες συνέπειες.

  1. . Το γεγονός ότι το σημείο τομής των διαγωνίων ενός παραλληλογράμμου τις χωρίζει σε δύο πανομοιότυπα μέρη είναι συνέπεια των σημείων ισότητας και επιδέχεται απόδειξη Οι πλευρές του πρόσθετου τριγώνου (με κατοπτρική κατασκευή, όπως στις αποδείξεις που εκτελέσαμε) είναι οι πλευρές της κύριας (οι πλευρές του παραλληλογράμμου).
  2. Αν υπάρχουν δύο ορθογώνια τρίγωνα που έχουν το ίδιο αιχμηρές γωνίες, τότε είναι παρόμοια. Αν το πόδι του πρώτου είναι ίσο με το πόδι του δεύτερου, τότε είναι ίσα. Αυτό είναι αρκετά εύκολο να γίνει κατανοητό - όλα τα ορθογώνια τρίγωνα έχουν ορθή γωνία. Επομένως, τα σημάδια της ισότητας είναι πιο απλά για αυτούς.
  3. Δύο τρίγωνα με ορθές γωνίες, στα οποία δύο σκέλη έχουν το ίδιο μήκος, μπορούν να θεωρηθούν πανομοιότυπα. Αυτό οφείλεται στο γεγονός ότι η γωνία μεταξύ των δύο ποδιών είναι πάντα 90 μοίρες. Επομένως, σύμφωνα με το πρώτο κριτήριο (από δύο πλευρές και τη γωνία μεταξύ τους), όλα τα τρίγωνα με ορθές γωνίες και ίδια σκέλη είναι ίσα.
  4. Αν υπάρχουν δύο ορθογώνια τρίγωνα και το ένα τους σκέλος και η υποτείνουσα είναι ίσα, τότε τα τρίγωνα είναι ίδια.

Ας αποδείξουμε αυτό το απλό θεώρημα.

Υπάρχουν δύο ορθογώνια τρίγωνα. Το ένα έχει πλευρές a, b, c, όπου c είναι η υποτείνουσα. α, β - πόδια. Το δεύτερο έχει πλευρές n, m, l, όπου l είναι η υποτείνουσα. m, n - πόδια.

Σύμφωνα με το Πυθαγόρειο θεώρημα, ένα από τα σκέλη ισούται με:

;

.

Έτσι, αν n = a, l = c (ισότητα σκελών και υποτείνων), αντίστοιχα, τα δεύτερα σκέλη θα είναι ίσα. Οι αριθμοί, κατά συνέπεια, θα είναι ίσοι σύμφωνα με το τρίτο χαρακτηριστικό (σε τρεις πλευρές).

Ας σημειώσουμε μια ακόμη σημαντική συνέπεια. Αν υπάρχουν δύο ίσα τρίγωνα και είναι όμοια με συντελεστή ομοιότητας k, δηλαδή οι αναλογίες ανά ζεύγη όλων των πλευρών τους είναι ίσοι με k, τότε ο λόγος των εμβαδών τους είναι ίσος με k2.

Το πρώτο σημάδι ισότητας τριγώνων. Βίντεο μάθημα γεωμετρίας 7η τάξη

Γεωμετρία 7 Το πρώτο σημάδι ισότητας τριγώνων

συμπέρασμα

Το θέμα που συζητήσαμε θα βοηθήσει κάθε μαθητή να κατανοήσει καλύτερα τα βασικά γεωμετρικές έννοιεςκαι βελτιώστε τις δεξιότητές σας ο πιο ενδιαφέροντα κόσμοςμαθηματικά.

Από σχολικό μάθημαΣτη γεωμετρία, είναι γνωστό το πρόσημο ότι τα τρίγωνα είναι ίσα κατά μήκος δύο πλευρών και η γωνία μεταξύ τους, δηλαδή:

Εάν δύο πλευρές και η μεταξύ τους γωνία ενός τριγώνου είναι αντίστοιχα ίσες με δύο πλευρές και η μεταξύ τους γωνία ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα (Εικ. 1).

Είναι φυσικό να τίθεται το ερώτημα εάν τα τρίγωνα θα είναι ίσα εάν οι αντίστοιχες ίσες γωνίες στα τρίγωνα δεν περιέχονται μεταξύ ίσων πλευρών. Είναι αλήθεια ότι αν δύο πλευρές και μια γωνία ενός τριγώνου είναι αντίστοιχα ίσες με δύο πλευρές και μια γωνία ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα.

Αποδεικνύεται ότι αυτό δεν είναι αλήθεια. Ας δώσουμε ένα παράδειγμα. Σκεφτείτε έναν κύκλο και τη χορδή του ΑΒ (Εικ. 2). Με κέντρο στο σημείο Α, σχεδιάζουμε έναν άλλο κύκλο που τέμνει τον πρώτο κύκλο σε ορισμένα σημεία C και C 1. Τότε στα τρίγωνα ABC και ABC 1 Το AB είναι μια κοινή πλευρά, AC = AC 1,C =Από το 1, ωστόσο, τα τρίγωνα ABC και ABC 1 δεν είναι ίσα.

Στη διατύπωση σημείων ισότητας τριγώνων, μπορείτε να συμπεριλάβετε όχι μόνο πλευρές και γωνίες, αλλά και άλλα στοιχεία τριγώνων. Ας εξετάσουμε διάφορες διατυπώσεις κριτηρίων για την ισότητα των τριγώνων με τρία στοιχεία, συμπεριλαμβανομένων των πλευρών, των γωνιών, των υψών, των διχοτόμων και των διαμέσου των τριγώνων. Ας μάθουμε την εγκυρότητα των αντίστοιχων σημείων.

Εάν η γωνία, η πλευρά απέναντι από αυτή τη γωνία και το ύψος που πέφτει στην άλλη πλευρά ενός τριγώνου είναι αντίστοιχα ίσα με τη γωνία, την πλευρά και το ύψος ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα.

Αφήστε τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1 ΜΕ = ΜΕ 1 , ΑΒ = ΕΝΑ 1 σι 1, ύψος A.H.ίσο με το ύψος ΕΝΑ 1 H 1 (Εικ. 3). Ας αποδείξουμε ότι τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1 είναι ίσα.

Ορθογώνια τρίγωνα ABHΚαι ΕΝΑ 1 σι 1 HΤο 1 είναι ίσο στο πόδι και στην υποτείνουσα. Που σημαίνει, σι = σι 1 . Λαμβάνοντας υπ 'όψιν ότι ΜΕ = ΜΕ 1, έχουμε ισότητα ΕΝΑ = ΕΝΑ 1 . Έτσι, σε τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 Γ 1

ΑΒ= ΕΝΑ 1 σι 1 , ΕΝΑ = ΕΝΑ 1 , σι = σι 1 .

Επομένως, αυτά τα τρίγωνα είναι ίσα σε πλευρές και δύο παρακείμενες γωνίες.

Αφήστε τη γωνία, την πλευρά που γειτνιάζει με αυτή τη γωνία και το ύψος που χαμηλώνει στην άλλη πλευρά δίπλα στη δεδομένη γωνία ενός τριγώνου να είναι αντίστοιχα ίσα με τη γωνία, την πλευρά και το ύψος του άλλου τριγώνου (Εικ. 4).

Ας δώσουμε ένα παράδειγμα που δείχνει ότι η ισότητα των υποδεικνυόμενων στοιχείων των τριγώνων δεν επαρκεί για την ισότητα των ίδιων των τριγώνων.

Ας σκεφτούμε ορθογώνια τρίγωνα ABHΚαι ΕΝΑ 1 σι 1 H 1 (H = H 1 = 90 ο), στο οποίο

ΑΒ = ΕΝΑ 1 σι 1 , σι = σι 1 , A.H. = ΕΝΑ 1 H 1

(Εικ. 5). Στις συνέχειες των πλευρών B.H.Και σι 1 H 1 αφήστε κατά μέρος άνισα τμήματα HCΚαι H 1 ντο 1 . Στη συνέχεια σε τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1

ΑΒ = ΕΝΑ 1 σι 1 , σι = σι 1 ,

ύψη A.H.Και ΕΝΑ 1 HΤο 1 είναι ίσο, αλλά τα ίδια τα τρίγωνα δεν είναι ίσα.

Εάν δύο πλευρές και η διάμεσος που περικλείεται μεταξύ τους ενός τριγώνου είναι αντίστοιχα ίσες με δύο πλευρές και τη διάμεσο ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα.

Αφήστε τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1

ΜΕΤΑ ΧΡΙΣΤΟΝ.= ΕΝΑ 1 ντο 1 , ΠΡΟ ΧΡΙΣΤΟΥ. = σι 1 ντο 1 ,

διάμεσος SMίσο με διάμεσο C 1 Μ 1 (Εικ. 6). Ας αποδείξουμε ότι τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1 είναι ίσα.

Ας συνεχίσουμε τις διάμεσους και ας αφήσουμε στην άκρη τα τμήματα M.D. = ΕΚ.Και Μ 1 ρε 1 = ντο 1 Μ 1 (Εικ. 6).

Τετράπλευρα ACBDΚαι ΕΝΑ 1 ΜΕ 1 σι 1 ρε 1 - παραλληλόγραμμα. Τρίγωνα ACDΚαι ΕΝΑ 1 ντο 1 ρε

ACD = ΕΝΑ 1 ντο 1 ρε 1 .

Ομοίως, τρίγωνα BCDΚαι σι 1 ντο 1 ρεΤο 1 είναι ίσο σε τρεις πλευρές. Ως εκ τούτου,

BCD = σι 1 ντο 1 ρε 1 .

Που σημαίνει, ΜΕ = ΜΕ 1 και τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντοΤο 1 είναι ίσο και στις δύο πλευρές και η μεταξύ τους γωνία.


Έστω η γωνία, η πλευρά που γειτνιάζει με αυτήν τη γωνία και η διάμεσος που σύρεται σε αυτήν την πλευρά ενός τριγώνου είναι αντίστοιχα ίσες με τη γωνία, την πλευρά και τη διάμεσο ενός άλλου τριγώνου (Εικ. 7).


Θεωρήστε έναν κύκλο με κέντρο στο σημείο Μ(Εικ. 8). Ας σχεδιάσουμε δύο διαμέτρους ΑΒΚαι ΕΝΑ 1 σι 1 . Μέσα από τελείες ΕΝΑ, ΕΝΑ 1 , Μσχεδιάστε έναν άλλο κύκλο και επιλέξτε ένα σημείο πάνω του ντο, όπως φαίνεται στην εικόνα. Σε τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο

ΑΒ = ΕΝΑ 1 σι 1 , ΕΝΑ = ΕΝΑ 1 ,

διάμεσος Γ Μ αλφάβητοΚαι ΕΝΑ 1 σι 1 ντοόχι ίσα.

Εάν μια πλευρά και δύο διάμεσοι που σύρονται σε δύο άλλες πλευρές ενός τριγώνου είναι αντίστοιχα ίσες με μια πλευρά και δύο διάμεσους ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα.

Αφήστε τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1 ΑΒ = ΕΝΑ 1 σι 1, διάμεσος ΕΙΜΑΙ.ίσο με τη διάμεσο ΕΝΑ 1 Μ 1, διάμεσος B.K.ίσο με τη διάμεσο σι 1 κ 1 (Εικ. 9). Ας αποδείξουμε ότι τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1 είναι ίσα.

Πόντοι ΟΚαι Ο 1, οι τομές των διαμέσου αυτών των τριγώνων διαιρούν τις διάμεσους σε αναλογία 2:1, μετρώντας από την κορυφή. Τρίγωνα λοιπόν ABOΚαι ΕΝΑ 1 σι 1 ΟΤο 1 είναι ίσο σε τρεις πλευρές. Ως εκ τούτου,

BAO = σι 1 ΕΝΑ 1 Ο 1 ,

αυτό σημαίνει τρίγωνα A.B.M.Και ΕΝΑ 1 σι 1 ΜΤο 1 είναι ίσο και στις δύο πλευρές και η μεταξύ τους γωνία. Να γιατί

αλφάβητο = ΕΝΑ 1 σι 1 ντο 1 .

Ομοίως, αποδεικνύεται ότι

BAC = σι 1 ΕΝΑ 1 ντο 1 .

Τα τρίγωνα λοιπόν αλφάβητοΚαι ΕΝΑ 1 σι 1 ντοΤο 1 είναι ίσο σε πλευρές και δύο παρακείμενες γωνίες.


Έστω η γωνία και οι δύο διάμεσοι που σύρονται στις πλευρές του ενός τριγώνου αντίστοιχα με τη γωνία και δύο διάμεσους ενός άλλου τριγώνου (Εικ. 10).


Ας δώσουμε ένα παράδειγμα που δείχνει ότι η ισότητα των υποδεικνυόμενων στοιχείων δεν αρκεί για την ισότητα των ίδιων των τριγώνων.

Για να το κάνετε αυτό, σκεφτείτε δύο ίσους κύκλουςμε κέντρα στα σημεία Ο 1 και Ο 2 που αγγίζουν το ένα το άλλο σε ένα σημείο Μ(Εικ. 11).

Ας σχεδιάσουμε μια συγχορδία σε ένα από αυτά ΑΒκαι άμεση ΕΙΜΑΙ., τέμνοντας τον δεύτερο κύκλο σε κάποιο σημείο ντο. Ας σχεδιάσουμε ένα τμήμα ΠΡΟ ΧΡΙΣΤΟΥ.. Παίρνουμε ένα τρίγωνο αλφάβητο. Ας σχεδιάσουμε μια διάμεσο σε αυτό CKκαι δηλώνουν Οένα σημείο που το διαιρεί σε αναλογία 2:1, μετρώντας από την κορυφή ντο. Ας σχεδιάσουμε έναν κύκλο με το κέντρο στο σημείο Ο, ακτίνα κύκλου O.C., τέμνοντας τον δεύτερο κύκλο στο σημείο ντο 1 . Ας κάνουμε ένα άμεσο ντο 1 Μκαι δηλώνουν ΕΝΑ 1 το σημείο τομής του με τον πρώτο κύκλο. Ας υποδηλώσουμε κ 1 σημείο τομής συγχορδίας ΕΝΑ 1 σικαι ευθεία ντο 1 Ο. Σε τρίγωνα αλφάβητοΚαι ΕΝΑ 1 ΠΡΟ ΧΡΙΣΤΟΥ. 1 ΕΝΑ = ΕΝΑ 1, διάμεσος CKΚαι ντο 1 κ 1 ίσος, διάμεσος Β.Μ.- στρατηγός. Ωστόσο, τρίγωνα αλφάβητοΚαι ΕΝΑ 1 ΠΡΟ ΧΡΙΣΤΟΥ. 1 δεν είναι ίσα.

Εάν δύο πλευρές και η διχοτόμος μεταξύ τους ενός τριγώνου είναι αντίστοιχα ίσες με δύο πλευρές και τη διχοτόμο ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα.

Αφήστε τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1

ΜΕΤΑ ΧΡΙΣΤΟΝ.= ΕΝΑ 1 ντο 1 , ΠΡΟ ΧΡΙΣΤΟΥ. = σι 1 ντο 1 ,

διαχωριστική γραμμή CDίσο με τη διχοτόμο ΜΕ 1 ρε 1 . Ας αποδείξουμε ότι τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1 είναι ίσα.

Ας συνεχίσουμε τις πλευρές ΜΕΤΑ ΧΡΙΣΤΟΝ.Και ΕΝΑ 1 ντο 1 και σχεδιάστε τα τμήματα στις συνέχειές τους C.E. = ΠΡΟ ΧΡΙΣΤΟΥ.Και ντο 1 μι 1 = σι 1 ντο 1 (Εικ. 12). Επειτα

Τρίγωνα B.C.E.Και σι 1 ντο 1 μιΤο 1 είναι ίσο σε τρεις πλευρές. Που σημαίνει, μι = μι 1 και ΕΙΝΑΙ = σι 1 μι 1 . Τρίγωνα ABEΚαι ΕΝΑ 1 σι 1 μιΤο 1 είναι ίσο και στις δύο πλευρές και η μεταξύ τους γωνία. Που σημαίνει, ΑΒ = ΕΝΑ 1 σι 1 . Τα τρίγωνα λοιπόν αλφάβητοΚαι ΕΝΑ 1 σι 1 ντοΤο 1 είναι ίσο σε τρεις πλευρές.


Έστω η γωνία, η πλευρά που γειτνιάζει με αυτή τη γωνία και η διχοτόμος που σύρεται στην άλλη πλευρά δίπλα στη δεδομένη γωνία ενός τριγώνου αντίστοιχα με τη γωνία, την πλευρά και τη διχοτόμο ενός άλλου τριγώνου (Εικ. 13).


Παράδειγμα τριγώνων αλφάβητοΚαι αλφάβητο 1, που φαίνεται στο Σχήμα 14, δείχνει ότι η ισότητα των υποδεικνυόμενων στοιχείων δεν είναι αρκετή για την ισότητα των ίδιων των τριγώνων.

Πράγματι, σε τρίγωνα αλφάβητοΚαι αλφάβητο 1 σι- γενική, ΑΒ- κοινή πλευρά, διχοτόμοι ΕΝΑ ΔΚαι ΕΝΑ Δ 1 είναι ίσα. Ωστόσο, τρίγωνα αλφάβητοΚαι αλφάβητο 1 δεν είναι ίσα.

Αφήστε την πλευρά, τη διάμεσο και το ύψος που τραβιέται στις άλλες δύο πλευρές ενός τριγώνου να είναι αντίστοιχα ίσα με την πλευρά, τη διάμεσο και το ύψος του άλλου τριγώνου (Εικ. 15).


Ας δώσουμε ένα παράδειγμα που δείχνει ότι η ισότητα των υποδεικνυόμενων στοιχείων δεν αρκεί για την ισότητα των ίδιων των τριγώνων.

Για να το κάνετε αυτό, σκεφτείτε έναν κύκλο και μια γωνία με μια κορυφή στο κέντρο ΕΝΑαυτόν τον κύκλο (Εικ. 16). Ας βάλουμε ένα τμήμα στο πλάι του ΑΒ, μεγαλύτερη σε διάμετρο, και από τη μέση του κσχεδιάστε μια ευθεία γραμμή παράλληλη προς την άλλη πλευρά της γωνίας και τέμνουσα τον κύκλο σε ορισμένα σημεία ΜΚαι Μ 1 . Ας τραβήξουμε ευθείες γραμμές Β.Μ., Β.Μ. 1 και τα σημεία τομής τους με την πλευρά της γωνίας συμβολίζουμε ανάλογα ντοΚαι ντο 1 . Στη συνέχεια σε τρίγωνα αλφάβητοΚαι αλφάβητο 1 πλευρά ΑΒ- σύνολο, ύψος B.H.- σύνολο, διάμεσος ΕΙΜΑΙ.Και ΕΙΜΑΙ.Το 1 είναι ίσο, αλλά τα τρίγωνα αλφάβητοΚαι αλφάβητο 1 δεν είναι ίσα.

Δύο τρίγωνα είναι ίσα αν η πλευρά, η διάμεσος και το υψόμετρο που τραβιέται στην άλλη πλευρά ενός τριγώνου είναι αντίστοιχα ίσα με την πλευρά, τη διάμεσο και το ύψος του άλλου τριγώνου.

Αφήστε τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1 ΜΕΤΑ ΧΡΙΣΤΟΝ. = ΕΝΑ 1 ντο 1, διάμεσος ΕΚ.Και ντο 1 Μ 1 ίσο, ύψη CHΚαι ντο 1 H 1 είναι ίσα (Εικ. 17). Ας αποδείξουμε ότι τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1 είναι ίσα.

Πράγματι, ορθογώνια τρίγωνα ACHΚαι ΕΝΑ 1 ντο 1 HΤο 1 είναι ίσο σε υποτείνουσα και πόδι. Επομένως ο F ΕΝΑ= Φ ΕΝΑ 1 και A.H. = ΕΝΑ 1 H 1 . Ορθογώνια τρίγωνα CMHΚαι ντο 1 Μ 1 HΤο 1 είναι ίσο σε υποτείνουσα και πόδι. Ως εκ τούτου, Μ.Η. = Μ 1 H 1, από όπου ΕΙΜΑΙ. = ΕΝΑ 1 Μ 1 σημαίνει ΑΒ = ΕΝΑ 1 σι 1 . Τα τρίγωνα λοιπόν αλφάβητοΚαι ΕΝΑ 1 σι 1 ντοΤο 1 είναι ίσο και στις δύο πλευρές και η μεταξύ τους γωνία.


Δύο τρίγωνα είναι ίσα αν οι τρεις διάμεσοι ενός τριγώνου είναι αντίστοιχα ίσες με τις τρεις διάμεσες του άλλου τριγώνου.

Αφήστε τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1 είναι αντίστοιχα ίσα με τη διάμεσο Ο Α.Κ.Και ΕΝΑ 1 κ 1 , B.L.Και σι 1 μεγάλο 1 , ΕΚ.Και ντο 1 Μ 1 (Εικ. 18). Ας αποδείξουμε ότι τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1 είναι ίσα.

Αφήνω ΟΚαι Ο 1 - σημεία τομής των διάμεσων αυτών των τριγώνων. Σημειώστε ότι οι διάμεσοι ΟΜΚαι Ο 1 Μ 1 τρίγωνα ABOΚαι ΕΝΑ 1 σι 1 Ο 1 είναι ίσα, αφού αποτελούν το ένα τρίτο των αντίστοιχων διαμέσου αυτών των τριγώνων.

Σύμφωνα με το κριτήριο της ισότητας των τριγώνων, που αποδείξαμε στον αριθμό 3, τρίγωνα ABOΚαι ΕΝΑ 1 σι 1 Ο 1 είναι ίσα, που σημαίνει ΑΒ = ΕΝΑ 1 σι 1 .

Ομοίως, αποδεικνύεται ότι ΠΡΟ ΧΡΙΣΤΟΥ. = σι 1 ντο 1 και ΜΕΤΑ ΧΡΙΣΤΟΝ. = ΕΝΑ 1 ντο 1 . Τα τρίγωνα λοιπόν αλφάβητοΚαι ΕΝΑ 1 σι 1 ντοΤο 1 είναι ίσο σε τρεις πλευρές.


Δύο τρίγωνα είναι ίσα αν τα τρία ύψη ενός τριγώνου είναι αντίστοιχα ίσα με τα τρία ύψη του άλλου τριγώνου.

Αφήστε τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1 είναι αντίστοιχα ίσα με τα ύψη A.H.Και ΕΝΑ 1 H 1 , B.G.Και σι 1 σολ 1 , CFΚαι ντο 1 φά 1 (Εικ. 19). Ας αποδείξουμε ότι τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1 είναι ίσα.

Ας υποδηλώσουμε τις πλευρές των τριγώνων αντίστοιχα ένα, σι, ντοΚαι ένα 1 , σι 1 , ντο 1 και τα αντίστοιχα ύψη η α, β β, η γΚαι η 1ένα , η 1σι , η 1ντο. Υπάρχουν ισότητες αχ α = bh β = κεφ γΚαι ένα 1 η 1ένα = σι 1 η 1σι = ντο 1 η 1ντο. Διαιρώντας τις πρώτες ισότητες όρο προς όρο στη δεύτερη, λαμβάνουμε ισότητες από τις οποίες προκύπτει ότι τα τρίγωνα αλφάβητοΚαι ΕΝΑ 1 σι 1 ντο 1 είναι παρόμοια. Δεδομένου ότι τα αντίστοιχα ύψη αυτών των τριγώνων είναι ίσα, δεν είναι μόνο παρόμοια, αλλά και ίσα.