Εκπαιδευτικό και μεθοδολογικό εγχειρίδιο
να προετοιμαστούν για τις εξετάσεις του Ενιαίου Κράτους στα μαθηματικά

Η ΤΡΙΓΩΝΟΜΕΤΡΙΑ ΣΤΗ ΧΡΗΣΗ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ

Ο σκοπός αυτού του σεμιναρίου είναι να βοήθεια σε μαθητές στην προετοιμασία για την Ενιαία Κρατική Εξέταση στα μαθηματικά στην ενότητα "Τριγωνομετρία".

ΣΕ εγχειρίδιοδιενεργείται ανάλυση και δίνονται λύσεις σε τυπικά προβλήματα στην τριγωνομετρία που προσφέρει το Ινστιτούτο της Μόσχας ανοιχτή εκπαίδευσησε διάφορους ελέγχους, διαγνωστικούς, εκπαιδευτικούς, επίδειξης και τα χαρτιά των εξετάσεωνστα μαθηματικά για μαθητές της 10ης και 11ης τάξης.

Μετά την ανάλυση κάθε τυπικού προβλήματος, δίνονται παρόμοια προβλήματα για ανεξάρτητη επίλυση.

Με τα απαραίτητα θεωρητικές πληροφορίες, που χρησιμοποιείται για την επίλυση προβλημάτων, μπορείτε να βρείτε στην ενότητα «Τριγωνομετρία» του «Εγχειριδίου Μαθηματικών για Σχολικούς Μαθητές».

Με το κύριο μεθόδους λύσης τριγωνομετρικές εξισώσεις μπορείτε να μας γνωρίσετε στο δικό μας εκπαιδευτικό εγχειρίδιο«Επίλυση τριγωνομετρικών εξισώσεων».

Για μαθητές των τάξεων 10 και 11 που θέλουν να προετοιμαστούν καλά και να περάσουν Ενιαία κρατική εξέταση στα μαθηματικά ή τη ρωσική γλώσσαεπί υψηλή βαθμολογία, Το εκπαιδευτικό κέντροΗ «Resolventa» πραγματοποιεί μαθήματα προετοιμασίας για την Ενιαία Κρατική Εξέταση.

Διοργανώνουμε και για μαθητές

Με demo Επιλογές Ενιαίας Κρατικής Εξέτασης , που δημοσιεύτηκε στην επίσημη πύλη πληροφοριώνΕνας Κρατική Εξέταση, μπορείτε να βρείτε στο

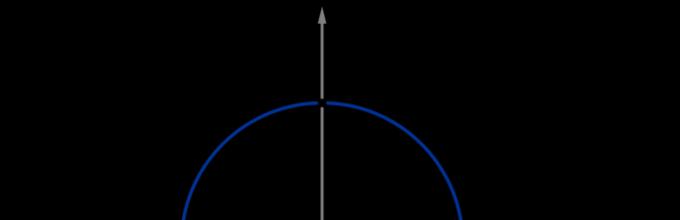
\(\blacktriangleright\) Θεωρούμε ένα ορθογώνιο σύστημα συντεταγμένων και σε αυτό έναν κύκλο με μοναδιαία ακτίνα και κέντρο στην αρχή.

Γωνία στο \(1^\circ\)- είναι έτσι επίκεντρη γωνία, το οποίο στηρίζεται σε ένα τόξο του οποίου το μήκος είναι ίσο με το \(\dfrac1(360)\) το μήκος ολόκληρου του κύκλου.

\(\μαύρο τρίγωνο\) Θα εξετάσουμε τις γωνίες στον κύκλο στον οποίο η κορυφή βρίσκεται στο κέντρο του κύκλου και η μία πλευρά συμπίπτει πάντα με τη θετική κατεύθυνση του άξονα \(Ox\) (επισημαίνεται με κόκκινο χρώμα στο σχήμα) .
Οι γωνίες σημειώνονται με αυτόν τον τρόπο \(45^\circ,\ 180^\circ,\ 240^\circ\):

Σημειώστε ότι η γωνία \(0^\circ\) είναι μια γωνία της οποίας και οι δύο πλευρές συμπίπτουν με τη θετική κατεύθυνση του άξονα \(Ox\) .

Το σημείο στο οποίο η δεύτερη πλευρά μιας τέτοιας γωνίας \(\άλφα\) τέμνει τον κύκλο θα ονομάζεται \(P_(\alpha)\) .
Η θέση του σημείου \(P_(0)\) θα ονομάζεται αρχική θέση.

Έτσι, μπορούμε να πούμε ότι περιστρέφουμε σε κύκλο από την αρχική θέση \(P_0\) στη θέση \(P_(\alpha)\) κατά μια γωνία \(\alpha\) .

\(\μαύρο τρίγωνο\) Μια αριστερόστροφη περιστροφή σε κύκλο είναι μια θετική περιστροφή. Μια περιστροφή δεξιόστροφα είναι μια αρνητική περιστροφή.

Για παράδειγμα, στο σχήμα σημειώνονται οι γωνίες \(-45^\circ, -90^\circ, -160^\circ\):

\(\μαύρο τρίγωνο\) Θεωρήστε το σημείο \(P_(30^\circ)\) σε έναν κύκλο. Για να περιστρέψετε σε κύκλο από την αρχική θέση στο σημείο \(P_(30^\circ)\), πρέπει να περιστρέψετε τη γωνία \(30^\circ\) (πορτοκαλί). Αν κάνουμε μια πλήρη περιστροφή (δηλαδή κατά \(360^\circ\) ) και άλλη μια στροφή κατά \(30^\circ\) , τότε θα φτάσουμε πάλι σε αυτό το σημείο, αν και έχουμε ήδη κάνει μια στροφή κατά μια γωνία \(390^\circ=360^\circ+30^\circ\)(μπλε). Μπορούμε επίσης να φτάσουμε σε αυτό το σημείο κάνοντας μια στροφή στο \(-330^\circ\) (πράσινο), στο \(750^\circ=360^\circ+360^\circ+30^\circ\)και τα λοιπά.

Έτσι, κάθε σημείο του κύκλου αντιστοιχεί σε έναν άπειρο αριθμό γωνιών, και αυτές οι γωνίες διαφέρουν μεταξύ τους κατά έναν ακέραιο αριθμό πλήρων περιστροφών ( \(n\cdot360^\circ, n\in\mathbb(Z)\)).
Για παράδειγμα, η γωνία \(30^\circ\) είναι \(360^\circ\) μεγαλύτερη από τη γωνία \(-330^\circ\) και \(2\cdot 360^\circ\) μικρότερη από τη γωνία \(750^\circ\) .

Όλες οι γωνίες που βρίσκονται στο σημείο \(P_(30^\circ)\) μπορούν να γραφτούν με τη μορφή: \(\alpha=30^\circ+n\cdot 360^\circ, \n\in\mathbb(Z)\).

\(\μαύρο τρίγωνο\) Γωνία σε \(1\) ακτίνια- αυτή είναι η κεντρική γωνία που στηρίζεται σε ένα τόξο του οποίου το μήκος είναι ίσο με την ακτίνα του κύκλου:

Επειδή το μήκος ολόκληρου του κύκλου με ακτίνα \(R\) είναι ίσο με \(2\pi R\), και σε μέτρο μοίρας - \(360^\circ\), τότε έχουμε \(360^\circ=2\pi \cdot 1\textbf(rad)\), που \ Αυτός είναι ο βασικός τύπος με τον οποίο μπορείτε να μετατρέψετε μοίρες σε ακτίνια και αντίστροφα.

Παράδειγμα 1.Βρείτε το μέτρο του ακτινίου της γωνίας \(60^\circ\) .

Επειδή \(180^\circ = \pi \Rightarrow 1^\circ = \dfrac(\pi)(180) \Rightarrow 60^\circ=\dfrac(\pi)3\)

Παράδειγμα 2.Εύρημα μέτρο βαθμούγωνία \(\dfrac34 \pi\) .

Επειδή \(\pi=180^\circ \Δεξί βέλος \dfrac34 \pi=\dfrac34 \cdot 180^\circ=135^\circ\).

Συνήθως γράφουν, για παράδειγμα, όχι \(\dfrac(\pi)4 \text(rad)\), αλλά απλώς \(\dfrac(\pi)4\) (δηλαδή η μονάδα μέτρησης "rad" παραλείπεται). Σημειώστε ότι ο προσδιορισμός των μοιρών όταν γράφετε μια γωνία μην χαμηλώνεις. Έτσι, γράφοντας «η γωνία είναι ίση με \(1\)» εννοούμε ότι «η γωνία είναι ίση με \(1\) ακτίνια», και όχι «η γωνία είναι ίση με \(1\) μοίρες».

Επειδή \(\pi \πάχος περίπου 3,14 \Δεξί βέλος 180^\circ \χάχος κατά προσέγγιση 3,14 \textbf(rad) \Δεξί βέλος 1 \textbf(rad) \πάχος κατά προσέγγιση 57^\circ\).
Μια τέτοια κατά προσέγγιση αντικατάσταση δεν μπορεί να γίνει σε προβλήματα, αλλά η γνώση του τι \(1\) ακτίνων σε μοίρες είναι περίπου ίσο με συχνά βοηθά στην επίλυση ορισμένων προβλημάτων. Για παράδειγμα, με αυτόν τον τρόπο είναι ευκολότερο να βρεθεί μια γωνία \(5\) ακτίνων σε έναν κύκλο: είναι περίπου ίση με \(285^\circ\) .

\(\μαύρο τρίγωνο\) Από την πορεία της επιπεδομετρίας (γεωμετρία σε επίπεδο) γνωρίζουμε ότι για γωνίες \(0<\alpha< 90^\circ\) определены синус, косинус, тангенс и котангенс следующим образом:
αν δοθεί ένα ορθογώνιο τρίγωνο με πλευρές \(a, b, c\) και γωνία \(\άλφα\), τότε:

Επειδή Οποιεσδήποτε γωνίες ορίζονται στον μοναδιαίο κύκλο \(\alpha\in(-\infty;+\infty)\), τότε πρέπει να προσδιορίσετε το ημίτονο, το συνημίτονο, την εφαπτομένη και την συνεφαπτομένη για οποιαδήποτε γωνία.
Θεωρήστε τον μοναδιαίο κύκλο και πάνω του τη γωνία \(\alpha\) και το αντίστοιχο σημείο \(P_(\alpha)\):

Ας χαμηλώσουμε την κάθετο \(P_(\alpha)K\) από το σημείο \(P_(\alpha)\) στον άξονα \(Ox\) . Παίρνουμε ένα ορθογώνιο τρίγωνο \(\τρίγωνο OP_(\alpha)K\) από το οποίο έχουμε: \[\sin\alpha=\dfrac(P_(\alpha)K)(P_(\alpha)O) \qquad \cos \alpha=\dfrac(OK)(P_(\alpha)O)\]Σημειώστε ότι το τμήμα \(OK\) δεν είναι τίποτα άλλο από την τετμημένη \(x_(\alpha)\) του σημείου \(P_(\alpha)\) και το τμήμα \(P_(\alpha)K\) είναι η τεταγμένη \(y_(\άλφα)\) . Σημειώστε επίσης ότι από τότε πήραμε τον μοναδιαίο κύκλο, τότε \(P_(\alpha)O=1\) είναι η ακτίνα του.
Ετσι, \[\sin\alpha=y_(\alpha), \qquad \cos \alpha=x_(\alpha)\]

Έτσι, αν το σημείο \(P_(\alpha)\) είχε συντεταγμένες \((x_(\alpha)\,;y_(\alpha))\), τότε μέσω της αντίστοιχης γωνίας οι συντεταγμένες του μπορούν να ξαναγραφούν ως \(( \ cos\alpha\,;\sin\alpha)\) .

Ορισμός: 1. Το ημίτονο της γωνίας \(\άλφα\) είναι η τεταγμένη του σημείου \(P_(\άλφα)\) που αντιστοιχεί σε αυτή τη γωνία στον μοναδιαίο κύκλο.

2. Το συνημίτονο της γωνίας \(\άλφα\) είναι η τετμημένη του σημείου \(P_(\άλφα)\) που αντιστοιχεί σε αυτή τη γωνία στον μοναδιαίο κύκλο.

Επομένως, ο άξονας \(Oy\) ονομάζεται άξονας των ημιτόνων, ο άξονας \(Ox\) ονομάζεται άξονας των συνημιτόνων.

\(\μαύρο τρίγωνο\) Ο κύκλος μπορεί να χωριστεί σε \(4\) τέταρτα, όπως φαίνεται στο σχήμα.

Επειδή στο τέταρτο \(I\) τόσο η τετμημένη όσο και οι τεταγμένες όλων των σημείων είναι θετικά, τότε τα συνημίτονο και τα ημίτονο όλων των γωνιών από αυτό το τέταρτο είναι επίσης θετικά.
Επειδή στο \(II\) τέταρτο, οι τεταγμένες όλων των σημείων είναι θετικές και οι τετμημένες είναι αρνητικές, τότε τα συνημίτονα όλων των γωνιών από αυτό το τέταρτο είναι αρνητικά και τα ημίτονο είναι θετικά.
Ομοίως, μπορείτε να προσδιορίσετε το πρόσημο του ημιτόνου και του συνημιτονοειδούς για τα υπόλοιπα τέταρτα.

Παράδειγμα 3.Εφόσον, για παράδειγμα, τα σημεία \(P_(\frac(\pi)(6))\) και \(P_(-\frac(11\pi)6)\) συμπίπτουν, τότε οι συντεταγμένες τους είναι ίσες, δηλ. \(\sin\dfrac(\pi)6=\sin \left(-\dfrac(11\pi)6\right),\ \cos \dfrac(\pi)6=\cos \left(-\dfrac( 11\pi)6\δεξιά)\).

Παράδειγμα 4.Εξετάστε τα σημεία \(P_(\alpha)\) και \(P_(\pi-\alpha)\) . Αφήστε για ευκολία ας \(0<\alpha<\dfrac{\pi}2\) .

Ας σχεδιάσουμε κάθετες στον άξονα \(Ox\) : \(OK\) και \(OK_1\) . Τα τρίγωνα \(OKP_(\alpha)\) και \(OK_1P_(\pi-\alpha)\) είναι ίσα σε υποτείνουσα και γωνία ( \(\γωνία P_(\alpha)OK=\γωνία P_(\pi-\alpha)OK_1=\alpha\)). Ως εκ τούτου, \(OK=OK_1, KP_(\alpha)=K_1P_(\pi-\alpha)\). Επειδή σημειακές συντεταγμένες \(P_(\alpha)=(OK;KP_(\alpha))=(\cos\alpha\,;\sin\alpha)\), και τα σημεία \(P_(\pi-\alpha)=(-OK_1;K_1P_(\pi-\alpha))=(\cos(\pi-\alpha)\,;\sin(\pi-\alpha))\), ως εκ τούτου, \[\cos(\pi-\alpha)=-\cos\alpha, \qquad \sin(\pi-\alpha)=\sin\alpha\]

Με αυτόν τον τρόπο καλούνται άλλοι τύποι φόρμουλες μείωσης: \[(\large(\begin(array)(l|r) \hline \sin(\pi-\alpha)=\sin\alpha & \cos(\pi-\alpha)=-\cos\alpha\\ \sin(\pi+\alpha)=-\sin\alpha & \cos(\pi+\alpha)=-\cos\alpha\\ \sin(2\pi\pm\alpha)=\pm\sin\alpha & \cos (2\pi\pm\alpha)=\cos\alpha\\ \sin \left(\dfrac(\pi)2\pm\alpha\right)=\cos\alpha & \cos\left(\dfrac (\pi)2\pm\alpha\right)=\pm\sin\alpha\\ \hline \end(array)))\]

Χρησιμοποιώντας αυτούς τους τύπους, μπορείτε να βρείτε το ημίτονο ή το συνημίτονο οποιασδήποτε γωνίας, μειώνοντας αυτήν την τιμή στο ημίτονο ή συνημίτονο της γωνίας από το τέταρτο \(I\).

Πίνακας ημιτόνων, συνημιτόνων, εφαπτομένων και συνεφαπτομένων γωνιών από το πρώτο τέταρτο:
\[(\large(\begin(array)(|c|c|c|c|c|c|) \hline &&&&&\\[-17pt] & \quad 0 \quad (0^ \circ)& \quad \dfrac(\pi)6 \quad (30^\circ) & \quad \dfrac(\pi)4 \quad (45^\circ) & \quad \dfrac(\pi)3 \quad (60^\circ )& \quad \dfrac(\pi)2 \quad (90^\circ) \\ &&&&&\\[-17pt] \hline \sin & 0 &\frac12&\frac(\sqrt2)2&\frac(\sqrt3) 2&1\\ \hline \cos &1&\frac(\sqrt3)2&\frac(\sqrt2)2&\frac12&0\\ \hline \mathrm(tg) &0 &\frac(\sqrt3)3&1&\sqrt3&\infty\\ \hline \mathrm(ctg) &\infty &\sqrt3&1&\frac(\sqrt3)3&0\\ \hline \end(πίνακας))\]

Σημειώστε ότι αυτές οι τιμές εμφανίζονται στην ενότητα «Γεωμετρία σε επίπεδο (πλανομετρία). Μέρος II» στο θέμα «Αρχικές πληροφορίες για το ημίτονο, το συνημίτονο, την εφαπτομένη και την συνεφαπτομένη».

Παράδειγμα 5.Βρείτε το \(\sin(\dfrac(3\pi)4)\) .

Ας μετατρέψουμε τη γωνία: \(\dfrac(3\pi)4=\dfrac(4\pi-\pi)(4)=\pi-\dfrac(\pi)4\)

Ετσι, \(\sin(\dfrac(3\pi)4)=\sin\left(\pi-\dfrac(\pi)4\right)=\sin\dfrac(\pi)4=\dfrac(\sqrt2) 2\).

\(\blacktriangleright\) Για να διευκολύνετε την απομνημόνευση και τη χρήση τύπων μείωσης, μπορείτε να ακολουθήσετε τον ακόλουθο κανόνα.

Περίπτωση 1.\(n\cdot \pi\pm \alpha\) \[\sin(n\cdot \pi\pm \alpha)=\bigodot \sin\alpha\] \[\cos(n\cdot \pi\pm \alpha)=\bigodot \cos\alpha\]

Το πρόσημο μιας γωνίας μπορεί να βρεθεί προσδιορίζοντας σε ποιο τεταρτημόριο βρίσκεται. Χρησιμοποιώντας αυτόν τον κανόνα, υποθέτουμε ότι η γωνία \(\alpha\) βρίσκεται στο \(I\) τεταρτημόριο.

Περίπτωση 2.Εάν η γωνία μπορεί να αναπαρασταθεί με τη μορφή , όπου \(n\in\mathbb(N)\) , τότε \[\sin(n\cdot \pi+\dfrac(\pi)2\pm \alpha)=\bigodot \cos\alpha\]όπου στη θέση του \(\bigodot\) είναι το πρόσημο του ημιτόνου της γωνίας \(n\cdot \pi\pm \alpha\) . \[\cos(n\cdot \pi+\dfrac(\pi)2\pm \alpha)=\bigodot \sin\alpha\]όπου στη θέση του \(\bigodot\) είναι το πρόσημο του συνημιτόνου της γωνίας \(n\cdot \pi\pm \alpha\) .

Το πρόσημο καθορίζεται με τον ίδιο τρόπο όπως στην περίπτωση του \(1\) .

Σημειώστε ότι στην πρώτη περίπτωση η συνάρτηση παραμένει αμετάβλητη, και στη δεύτερη περίπτωση αλλάζει (λένε ότι η συνάρτηση αλλάζει σε συνάρτηση).

Παράδειγμα 6.Βρείτε το \(\sin \dfrac(13\pi)(3)\) .

Ας μετατρέψουμε τη γωνία: \(\dfrac(13\pi)(3)=\dfrac(12\pi+\pi)(3)=4\pi+\dfrac(\pi)3\), ως εκ τούτου, \(\sin \dfrac(13\pi)(3)=\sin \left(4\pi+\dfrac(\pi)3\right)=\sin\dfrac(\pi)3=\dfrac(\sqrt3) 2\)

Παράδειγμα 7.Βρείτε το \(\cos \dfrac(17\pi)(6)\) .

Ας μετατρέψουμε τη γωνία: \(\dfrac(17\pi)(6)=\dfrac(18\pi-\pi)(6)=3\pi-\dfrac(\pi)6\), ως εκ τούτου, \(\cos \dfrac(17\pi)(6)=\cos \left(3\pi-\dfrac(\pi)6\right)=-\cos\dfrac(\pi)6=-\dfrac( \sqrt3)2\)

\(\μαύρο τρίγωνο\) Εύρος τιμών ημιτόνου και συνημιτόνου.
Επειδή οι συντεταγμένες \(x_(\alpha)\) και \(y_(\alpha)\) οποιουδήποτε σημείου \(P_(\alpha)\) στον κύκλο μονάδας βρίσκονται στην περιοχή από \(-1\) έως \ (1\) , και \(\cos\alpha\) και \(\sin\alpha\) είναι η τετμημένη και η τεταγμένη, αντίστοιχα, αυτού του σημείου, τότε \[(\large(-1\leq \cos\alpha\leq 1 ,\qquad -1\leq\sin\alpha\leq 1))\]

Από ορθογώνιο τρίγωνο σύμφωνα με το Πυθαγόρειο θεώρημα έχουμε: \(x^2_(\άλφα)+y^2_(\άλφα)=1^2\)
Επειδή \(x_(\alpha)=\cos\alpha,\ y_(\alpha)=\sin\alpha \Rightarrow\) \[(\large(\sin^2\alpha+\cos^2\alpha=1)) - \textbf(βασική τριγωνομετρική ταυτότητα (GTT))\]

\(\μαύρο τρίγωνο\) Εφαπτομένη και συνεφαπτομένη.

Επειδή \(\mathrm(tg)\,\alpha=\dfrac(\sin\alpha)(\cos\alpha), \cos\alpha\ne 0\)

\(\mathrm(ctg)\,\alpha=\dfrac(\cos\alpha)(\sin\alpha), \sin\alpha\ne 0\), Οτι:

1) \((\large(\mathrm(tg)\,\alpha\cdot \mathrm(ctg)\,\alpha=1, \cos\alpha\ne 0, \sin\alpha \ne 0))\)

2) η εφαπτομένη και η συνεφαπτομένη είναι θετικές στα \(I\) και \(III\) τέταρτα και αρνητικές στα \(II\) και \(IV\) τέταρτα.

3) το εύρος τιμών της εφαπτομένης και της συνεφαπτομένης - όλοι οι πραγματικοί αριθμοί, δηλ. \(\mathrm(tg)\,\alpha\in\mathbb(R), \ \mathrm(ctg)\,\alpha\in\mathbb(R)\)

4) Οι τύποι αναγωγής ορίζονται επίσης για την εφαπτομένη και την συνεφαπτομένη.

Περίπτωση 1. \[\mathrm(tg)\,(n\cdot \pi\pm \alpha)=\bigodot \mathrm(tg)\,\alpha\]όπου στη θέση του \(\bigodot\) είναι το πρόσημο της εφαπτομένης της γωνίας \(n\cdot \pi\pm \alpha\) (\(\cos\alpha\ne 0\) ). \[\mathrm(ctg)\,(n\cdot \pi\pm \alpha)=\bigodot \mathrm(ctg)\,\alpha\]όπου στη θέση του \(\bigodot\) είναι το πρόσημο της συνεφαπτομένης γωνίας \(n\cdot \pi\pm \alpha\) (\(\sin\alpha\ne 0\) ).

Περίπτωση 2.Αν η γωνία μπορεί να παρασταθεί ως \(n\cdot \pi+\dfrac(\pi)2\pm\alpha\), όπου \(n\in\mathbb(N)\) , τότε \[\mathrm(tg)\,(n\cdot \pi+\dfrac(\pi)2\pm \alpha)=\bigodot \mathrm(ctg)\,\alpha\]όπου στη θέση \(\bigodot\) υπάρχει πρόσημο της εφαπτομένης της γωνίας \(n\cdot \pi\pm \alpha\) (\(\sin\alpha\ne 0\) ). \[\mathrm(ctg)\,(n\cdot \pi+\dfrac(\pi)2\pm \alpha)=\bigodot \mathrm(tg)\,\alpha\]όπου στη θέση του \(\bigodot\) είναι το πρόσημο της συνεφαπτομένης γωνίας \(n\cdot \pi\pm \alpha\) (\(\cos\alpha\ne 0\) ).

5) ο άξονας της εφαπτομένης διέρχεται από το σημείο \((1;0)\) παράλληλο με τον ημιτονοειδή άξονα και η θετική κατεύθυνση του άξονα της εφαπτομένης συμπίπτει με τη θετική κατεύθυνση του άξονα ημιτόνου.
ο άξονας της συνεφαπτομένης διέρχεται από το σημείο \((0;1)\) παράλληλο προς τον άξονα συνημιτόνου και η θετική κατεύθυνση του άξονα συνεφαπτομένης συμπίπτει με τη θετική κατεύθυνση του άξονα συνημιτόνου.

Θα δώσουμε μια απόδειξη αυτού του γεγονότος χρησιμοποιώντας το παράδειγμα του άξονα της εφαπτομένης.

\(\triangle OP_(\alpha)K \sim \triangle AOB \Rightarrow \dfrac(P_(\alpha)K)(OK)=\dfrac(BA)(OB) \Rightarrow \dfrac(\sin\alpha)( \cos\alpha)=\dfrac(BA)1 \Δεξί βέλος BA=\mathrm(tg)\,\alpha\).

Έτσι, εάν το σημείο \(P_(\alpha)\) συνδέεται με μια ευθεία γραμμή στο κέντρο του κύκλου, τότε αυτή η ευθεία γραμμή θα τέμνει την εφαπτομένη σε ένα σημείο του οποίου η τιμή είναι \(\mathrm(tg)\ ,\άλφα\) .

6) οι ακόλουθοι τύποι προκύπτουν από την κύρια τριγωνομετρική ταυτότητα: \ Ο πρώτος τύπος προκύπτει διαιρώντας τη δεξιά και την αριστερή πλευρά του OTT με το \(\cos^2\alpha\), ο δεύτερος διαιρώντας με το \(\sin^2\alpha\) .

Σημειώστε ότι η εφαπτομένη δεν ορίζεται σε γωνίες όπου το συνημίτονο είναι μηδέν (αυτό είναι \(\alpha=\dfrac(\pi)2+\pi n, n\in\mathbb(Z)\));
η συνεφαπτομένη δεν ορίζεται σε γωνίες όπου το ημίτονο είναι μηδέν (αυτό είναι \(\alpha=\pi+\pi n, n\in\mathbb(Z)\)).

\(\μαύρο τρίγωνο\) Ομοιότητα συνημιτονοειδούς και περιττότητα ημιτόνου, εφαπτομένη, συνεφαπτομένη.

Θυμηθείτε ότι μια συνάρτηση \(f(x)\) καλείται ακόμα κι αν \(f(-x)=f(x)\) .

Μια συνάρτηση ονομάζεται περιττή αν \(f(-x)=-f(x)\) .

Μπορεί να φανεί από τον κύκλο ότι το συνημίτονο της γωνίας \(\alpha\) είναι ίσο με το συνημίτονο της γωνίας \(-\alpha\) για οποιεσδήποτε τιμές του \(\alpha\):

Έτσι, το συνημίτονο είναι μια άρτια συνάρτηση, που σημαίνει ότι ο τύπος \[(\Large(\cos(-x)=\cos x))\] είναι αληθής

Είναι σαφές από τον κύκλο ότι το ημίτονο της γωνίας \(\alpha\) είναι αντίθετο από το ημίτονο της γωνίας \(-\alpha\) για οποιεσδήποτε τιμές του \(\alpha\) :

Έτσι, το ημίτονο είναι μια περιττή συνάρτηση, που σημαίνει ότι ο τύπος είναι σωστός \[(\Μεγάλο(\sin(-x)=-\sin x))\]

Η εφαπτομένη και η συνεφαπτομένη είναι επίσης περιττές συναρτήσεις: \[(\Μεγάλο(\mathrm(tg)\,(-x)=-\mathrm(tg)\,x))\] \[(\Μεγάλο(\mathrm(ctg)\,(-x)=-\mathrm(ctg)\,x))\]

Επειδή \(\mathrm(tg)\,(-x)=\dfrac(\sin (-x))(\cos(-x))=\dfrac(-\sin x)(\cos x)=-\mathrm (tg)\,x \qquad \mathrm(ctg)\,(-x)=\dfrac(\cos(-x))(\sin(-x))=-\mathrm(ctg)\,x\))

Όπως δείχνει η πρακτική, ένα από τα πιο δύσκολα τμήματα των μαθηματικών που συναντούν οι μαθητές στην Ενιαία Κρατική Εξέταση είναι η τριγωνομετρία. Η επιστήμη των αναλογιών διαστάσεων στα τρίγωνα αρχίζει να μαθαίνεται στην 8η τάξη. Οι εξισώσεις αυτού του τύπου περιέχουν μια μεταβλητή κάτω από το πρόσημο των τριγωνομετρικών συναρτήσεων. Παρά το γεγονός ότι τα πιο απλά από αυτά: \(sin x = a\) , \(cos x = a\) , \(tg x = a\) , \(ctg x = a\) - είναι γνωστά σχεδόν σε όλους μαθητής, η εφαρμογή τους είναι συχνά δύσκολη.

Στην Ενιαία Κρατική Εξέταση στα μαθηματικά σε επίπεδο προφίλ, μια σωστά λυμένη εργασία τριγωνομετρίας βαθμολογείται πολύ υψηλή. Ένας μαθητής μπορεί να λάβει έως και 4 βασικούς βαθμούς για τη σωστή ολοκλήρωση μιας εργασίας από αυτήν την ενότητα. Για να γίνει αυτό, η αναζήτηση φύλλων απάτης σχετικά με την τριγωνομετρία για τις εξετάσεις του Ενιαίου Κράτους είναι σχεδόν άσκοπη. Η πιο λογική λύση είναι να προετοιμαστείτε καλά για τις εξετάσεις.

Πως να το κάνεις?

Για να διασφαλίσετε ότι η τριγωνομετρία στην Εξέταση Ενιαίου Κράτους στα μαθηματικά δεν σας τρομάζει, χρησιμοποιήστε την πύλη μας κατά την προετοιμασία. Είναι βολικό, απλό και αποτελεσματικό. Σε αυτήν την ενότητα της εκπαιδευτικής μας πύλης, που είναι ανοιχτή σε μαθητές τόσο στη Μόσχα όσο και σε άλλες πόλεις, παρουσιάζεται με προσιτό τρόπο θεωρητικό υλικό και τύποι τριγωνομετρίας για την Ενιαία Κρατική Εξέταση. Επίσης, για όλους τους μαθηματικούς ορισμούς έχουμε επιλέξει παραδείγματα με αναλυτική περιγραφή της διαδικασίας επίλυσής τους.

Αφού μελετήσετε τη θεωρία στην ενότητα "Τριγωνομετρία" κατά την προετοιμασία για τις εξετάσεις του Ενιαίου Κράτους, συνιστούμε να μεταβείτε στους "Κατάλογους" ώστε οι γνώσεις που αποκτήθηκαν να αφομοιωθούν καλύτερα. Εδώ μπορείτε να επιλέξετε προβλήματα για ένα θέμα που σας ενδιαφέρει και να δείτε τις λύσεις τους. Έτσι, η επανάληψη της θεωρίας της τριγωνομετρίας στην Εξέταση του Ενιαίου Κράτους θα είναι όσο το δυνατόν πιο αποτελεσματική.

Τι πρέπει να ξέρετε;

Πρώτα απ 'όλα, πρέπει να μάθετε τις τιμές των οξέων γωνιών \(sin\) , \(cos\) , \(tg\) , \(ctg\) από \(0°\) έως \(90° \) . Επίσης, κατά την προετοιμασία για την Ενιαία Κρατική Εξέταση στη Μόσχα, αξίζει να θυμηθούμε τις βασικές μεθόδους επίλυσης προβλημάτων τριγωνομετρίας. Θα πρέπει να σημειωθεί ότι όταν ολοκληρώνετε εργασίες, πρέπει να μειώσετε την εξίσωση στην απλούστερη μορφή της. Μπορείτε να το κάνετε ως εξής:

παραγοντοποίηση της εξίσωσης?
αντικατάσταση μιας μεταβλητής (αναγωγή σε αλγεβρικές εξισώσεις).
που οδηγεί σε μια ομοιογενή εξίσωση.
μετακίνηση στη μισή γωνία.
μετατροπή προϊόντων σε ποσά·
εισάγοντας μια βοηθητική γωνία.
χρησιμοποιώντας την καθολική μέθοδο αντικατάστασης.

Σε αυτήν την περίπτωση, τις περισσότερες φορές ο μαθητής πρέπει να χρησιμοποιήσει αρκετές από τις μεθόδους που αναφέρονται κατά τη διάρκεια της λύσης.

Πίσω μπροστά

Προσοχή! Οι προεπισκοπήσεις διαφανειών είναι μόνο για ενημερωτικούς σκοπούς και ενδέχεται να μην αντιπροσωπεύουν όλα τα χαρακτηριστικά της παρουσίασης. Εάν ενδιαφέρεστε για αυτό το έργο, κατεβάστε την πλήρη έκδοση.

«Πες μου και θα ξεχάσω,
Δείξε μου και θα θυμηθώ
Συμμετάσχετε με και θα μάθω».
(Κινέζικη παροιμία)

Τα μαθηματικά έχουν γίνει εδώ και καιρό η γλώσσα της επιστήμης και της τεχνολογίας, και τώρα διεισδύουν ολοένα και περισσότερο στην καθημερινή ζωή και την καθημερινή γλώσσα, και εισάγονται όλο και περισσότερο σε τομείς που φαίνονται παραδοσιακά απομακρυσμένοι από αυτά. Η εντατική μαθηματοποίηση διαφόρων τομέων της ανθρώπινης δραστηριότητας έχει ενταθεί ιδιαίτερα με την ταχεία ανάπτυξη των υπολογιστών. Η μηχανογράφηση της κοινωνίας και η εισαγωγή σύγχρονων τεχνολογιών της πληροφορίας απαιτούν μαθηματική παιδεία ενός ατόμου σε κάθε χώρο εργασίας. Αυτό προϋποθέτει τόσο συγκεκριμένες μαθηματικές γνώσεις όσο και συγκεκριμένο στυλ σκέψης. Ειδικότερα, η εκμάθηση της τριγωνομετρίας είναι μια σημαντική πτυχή. Η μελέτη των τριγωνομετρικών συναρτήσεων χρησιμοποιείται ευρέως στην πράξη, στη μελέτη πολλών φυσικών διεργασιών, στη βιομηχανία, ακόμη και στην ιατρική. Στους μαθητές που θα χρησιμοποιούν τα μαθηματικά στις επαγγελματικές τους δραστηριότητες στο μέλλον πρέπει να παρέχεται υψηλή μαθηματική προετοιμασία.

Η τριγωνομετρία αποτελεί αναπόσπαστο μέρος του σχολικού μαθήματος των μαθηματικών. Η καλή γνώση και οι ισχυρές δεξιότητες στην τριγωνομετρία αποτελούν απόδειξη επαρκούς επιπέδου μαθηματικής κουλτούρας και απαραίτητη προϋπόθεση για την επιτυχή μελέτη των μαθηματικών, της φυσικής και ορισμένων τεχνικών κλάδων σε ένα πανεπιστήμιο. Ωστόσο, ένα σημαντικό ποσοστό αποφοίτων σχολείων αποκαλύπτει από χρόνο σε χρόνο πολύ κακή προετοιμασία σε αυτό το σημαντικό τμήμα των μαθηματικών, όπως αποδεικνύεται από τα αποτελέσματα των προηγούμενων ετών, καθώς μια ανάλυση της ενιαίας κρατικής εξέτασης έδειξε ότι οι μαθητές κάνουν πολλά λάθη όταν ολοκληρώνουν εργασίες σε αυτό το συγκεκριμένο τμήμα ή μην τα πάρετε καθόλου για τέτοιες εργασίες.

Αλλά ακόμη και οι Έλληνες, στην αυγή της ανθρωπότητας, θεωρούσαν την τριγωνομετρία την πιο σημαντική από τις επιστήμες, γιατί η γεωμετρία είναι η βασίλισσα των μαθηματικών και η τριγωνομετρία είναι η βασίλισσα της γεωμετρίας. Επομένως, εμείς, χωρίς να αμφισβητούμε τους αρχαίους Έλληνες, θα θεωρήσουμε την τριγωνομετρία μια από τις σημαντικότερες ενότητες του σχολικού μαθήματος και γενικότερα όλων των μαθηματικών επιστημών.

Η φυσική και η γεωμετρία δεν μπορούν να κάνουν χωρίς τριγωνομετρία. Η Ενιαία Κρατική Εξέταση δεν μπορεί να κάνει χωρίς τριγωνομετρία. Μόνο στο Μέρος Β, ερωτήσεις σχετικά με την τριγωνομετρία βρίσκονται σχεδόν στο ένα τρίτο των τύπων εργασιών. Αυτό περιλαμβάνει την επίλυση των απλούστερων τριγωνομετρικών εξισώσεων στην εργασία Β5 και την εργασία με τριγωνομετρικές εκφράσεις στην εργασία Β7 και τη μελέτη τριγωνομετρικών συναρτήσεων στην εργασία Β14, καθώς και τις εργασίες Β12, οι οποίες περιέχουν τύπους που περιγράφουν φυσικά φαινόμενα και περιέχουν τριγωνομετρικές συναρτήσεις. Είναι αδύνατο να μην σημειωθούν γεωμετρικές εργασίες, στη λύση των οποίων χρησιμοποιούνται οι ορισμοί του ημιτονοειδούς, συνημιτόνου, εφαπτομένης και συνεφαπτομένης οξείας γωνίας ορθογωνίου τριγώνου και βασικές τριγωνομετρικές ταυτότητες. Και αυτό είναι μόνο το μέρος Β! Υπάρχουν όμως και αγαπημένες τριγωνομετρικές εξισώσεις με επιλογή ριζών C1 και «όχι τόσο αγαπημένες» γεωμετρικές εργασίες C2 και C4.

Πώς μπορούν οι μαθητές να εκπαιδευτούν σε αυτά τα θέματα; Μπορεί να προσφερθεί ένας μεγάλος αριθμός μεθόδων, αλλά το πιο σημαντικό είναι ότι τα παιδιά δεν έχουν αίσθημα φόβου και περιττού άγχους, λόγω της τεράστιας ποικιλίας διαφορετικών εργασιών και τύπων. Και για αυτό είναι απαραίτητο να δημιουργηθεί μια θετική διάθεση κατά την επίλυση αυτών των εργασιών. Αυτή η παρουσίαση μπορεί να χρησιμοποιηθεί για τη διεξαγωγή μαθημάτων με μαθητές και για ομιλία σε σεμινάρια για μαθηματικούς στο πλαίσιο της προετοιμασίας για την Ενιαία Κρατική Εξέταση. Προσφέρει ορισμένους τύπους εργασιών και συζητά τις λύσεις τους.

Η καλή εκπαίδευση μπορεί να είναι όχι μόνο μια απλή λύση αυτών των εργασιών, αλλά και η συλλογή τους από τους ίδιους τους μαθητές. Ανάλογα με την προετοιμασία, αυτές μπορεί να είναι δοκιμές για την επίλυση περιορισμών στην επίλυση τριγωνομετρικών εξισώσεων C1, ακόμη και των ίδιων των εξισώσεων.

Μια άλλη ενεργή μέθοδος είναι η διεξαγωγή μαθημάτων με τη μορφή πνευματικών παιχνιδιών. Μία από τις πιο βολικές επιλογές, νομίζω, είναι η μορφή "Προσαρμοσμένο παιχνίδι". Αυτή η φόρμα παιχνιδιού, ειδικά τώρα με τη χρήση παρουσιάσεων υπολογιστή, μπορεί να χρησιμοποιηθεί κατά τη διάρκεια των δοκιμαστικών μαθημάτων, μετά τη μελέτη θεμάτων και κατά την προετοιμασία για την Ενιαία Κρατική Εξέταση. Η προτεινόμενη εργασία περιέχει «Το δικό σου παιχνίδι. Επίλυση τριγωνομετρικών εξισώσεων και ανισώσεων.»

Το αποτέλεσμα της προτεινόμενης εργασίας θα πρέπει να είναι η επιτυχής επίλυση εργασιών Ενιαίας Κρατικής Εξέτασης στο θέμα «Τριγωνομετρία».

Το μάθημα βίντεο "Get an A" περιλαμβάνει όλα τα απαραίτητα θέματα για την επιτυχή επιτυχία της Ενιαίας Κρατικής Εξέτασης στα μαθηματικά με 60-65 βαθμούς. Πλήρως όλες οι εργασίες 1-13 του Προφίλ Unified State Exam στα μαθηματικά. Κατάλληλο και για επιτυχία στη Βασική Ενιαία Κρατική Εξέταση στα μαθηματικά. Αν θέλετε να περάσετε τις εξετάσεις του Ενιαίου Κράτους με 90-100 μόρια, πρέπει να λύσετε το μέρος 1 σε 30 λεπτά και χωρίς λάθη!

Μάθημα προετοιμασίας για την Ενιαία Κρατική Εξέταση για τις τάξεις 10-11, καθώς και για εκπαιδευτικούς. Όλα όσα χρειάζεστε για να λύσετε το Μέρος 1 της Ενιαίας Κρατικής Εξέτασης στα μαθηματικά (τα πρώτα 12 προβλήματα) και το πρόβλημα 13 (τριγωνομετρία). Και αυτά είναι περισσότερα από 70 μόρια στην Ενιαία Κρατική Εξέταση και ούτε ένας μαθητής 100 βαθμών ούτε ένας φοιτητής ανθρωπιστικών επιστημών μπορεί να τα κάνει χωρίς αυτά.

Όλη η απαραίτητη θεωρία. Γρήγορες λύσεις, παγίδες και μυστικά της Ενιαίας Κρατικής Εξέτασης. Όλες οι τρέχουσες εργασίες του μέρους 1 από την τράπεζα εργασιών FIPI έχουν αναλυθεί. Το μάθημα συμμορφώνεται πλήρως με τις απαιτήσεις της Ενιαίας Κρατικής Εξέτασης 2018.

Το μάθημα περιέχει 5 μεγάλα θέματα, 2,5 ώρες το καθένα. Κάθε θέμα δίνεται από την αρχή, απλά και ξεκάθαρα.

Εκατοντάδες εργασίες Ενιαίας Κρατικής Εξέτασης. Προβλήματα λέξεων και θεωρία πιθανοτήτων. Απλοί και εύκολοι στην απομνημόνευση αλγόριθμοι για την επίλυση προβλημάτων. Γεωμετρία. Θεωρία, υλικό αναφοράς, ανάλυση όλων των τύπων εργασιών Ενιαίας Κρατικής Εξέτασης. Στερεομετρία. Δύσκολες λύσεις, χρήσιμα cheat sheets, ανάπτυξη χωρικής φαντασίας. Τριγωνομετρία από το μηδέν στο πρόβλημα 13. Κατανόηση αντί να στριμώχνω. Σαφείς εξηγήσεις περίπλοκων εννοιών. Αλγεβρα. Ρίζες, δυνάμεις και λογάριθμοι, συνάρτηση και παράγωγος. Μια βάση για την επίλυση σύνθετων προβλημάτων του Μέρους 2 της Ενιαίας Κρατικής Εξέτασης.

ΕΝΑ)Λύστε την εξίσωση 2(\sin x-\cos x)=tgx-1.

σι) \αριστερά[ \frac(3\pi )2;\,3\pi \δεξιά].

Δείξε λύση

Λύση

ΕΝΑ)Ανοίγοντας τις αγκύλες και μετακινώντας όλους τους όρους στην αριστερή πλευρά, παίρνουμε την εξίσωση 1+2 \sin x-2 \cos x-tg x=0. Λαμβάνοντας υπόψη ότι \cos x \neq 0, ο όρος 2 \sin x μπορεί να αντικατασταθεί από 2 tan x \cos x, λαμβάνουμε την εξίσωση 1+2 tg x \cos x-2 \cos x-tg x=0,που ομαδοποιώντας μπορεί να αναχθεί στη μορφή (1-tg x)(1-2 \cos x)=0.

1) 1-tg x=0, μαύρισμα x=1, x=\frac\pi 4+\pi n, n \in \mathbb Z;

2) 1-2 \cos x=0, \cos x=\frac12, x=\pm \frac\pi 3+2\pi n, n \in \mathbb Z.

σι)Χρησιμοποιώντας τον κύκλο αριθμών, επιλέξτε τις ρίζες που ανήκουν στο διάστημα \αριστερά[ \frac(3\pi )2;\, 3\pi \δεξιά].

x_1=\frac\pi 4+2\pi =\frac(9\pi )4,

x_2=\frac\pi 3+2\pi =\frac(7\pi )3,

x_3=-\frac\pi 3+2\pi =\frac(5\pi )3.

Απάντηση

ΕΝΑ) \frac\pi 4+\pi n, \pm\frac\pi 3+2\pi n, n \in \mathbb Z;

σι) \frac(5\pi )3, \frac(7\pi )3, \frac(9\pi )4.

Κατάσταση

ΕΝΑ)Λύστε την εξίσωση (2\sin ^24x-3\cos 4x)\cdot \sqrt (tgx)=0.

σι)Να αναφέρετε τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα \left(0;\,\frac(3\pi )2\right] ;

Δείξε λύση

Λύση

ΕΝΑ) ODZ: \begin(περιπτώσεις) tgx\geqslant 0\\x\neq \frac\pi 2+\pi k,k \in \mathbb Z. \end(περιπτώσεις)

Η αρχική εξίσωση στο ODZ είναι ισοδύναμη με ένα σύνολο εξισώσεων

\left[\!\!\begin(array)(l) 2 \sin ^2 4x-3 \cos 4x=0,\\tg x=0. \end(πίνακας)\δεξιά.

Ας λύσουμε την πρώτη εξίσωση. Για να γίνει αυτό θα κάνουμε μια αντικατάσταση \cos 4x=t, t \σε [-1; 1].Τότε \sin^24x=1-t^2. Παίρνουμε:

2(1-t^2)-3t=0,

2t^2+3t-2=0,

t_1=\frac12, t_2=-2, t_2\notin [-1; 1].

\cos 4x=\frac12,

4x=\pm\frac\pi 3+2\pi n,

x=\pm \frac\pi (12)+\frac(\pi n)2, n \in \mathbb Z.

Ας λύσουμε τη δεύτερη εξίσωση.

tg x=0,\, x=\pi k, k \in \mathbb Z.

Χρησιμοποιώντας τον κύκλο μονάδας, βρίσκουμε λύσεις που ικανοποιούν το ODZ.

Το σύμβολο «+» σηματοδοτεί το 1ο και 3ο τέταρτο, στα οποία tg x>0.

Παίρνουμε: x=\pi k, k \in \mathbb Z; x=\frac\pi (12)+\pi n, n \in \mathbb Z; x=\frac(5\pi )(12)+\pi m, m \in \mathbb Z.

σι)Ας βρούμε τις ρίζες που ανήκουν στο διάστημα \αριστερά(0;\,\frac(3\pi )2\δεξιά].

x=\frac\pi (12), x=\frac(5\pi )(12); x=\pi ; x=\frac(13\pi )(12); x=\frac(17\pi )(12).

Απάντηση

ΕΝΑ) \pi k, k \in \mathbb Z; \frac\pi (12)+\pi n, n \in \mathbb Z; \frac(5\pi )(12)+\pi m, m \in \mathbb Z.

σι) \πι; \frac\pi (12); \frac(5\pi )(12); \frac(13\pi )(12); \frac(17\pi )(12).

Πηγή: «Μαθηματικά. Προετοιμασία για την Ενιαία Κρατική Εξέταση 2017. Επίπεδο προφίλ." Εκδ. F. F. Lysenko, S. Yu. Kulabukhova.

Κατάσταση

ΕΝΑ)Λύστε την εξίσωση: \cos ^2x+\cos ^2\frac\pi 6=\cos ^22x+\sin ^2\frac\pi 3;

σι)Καταγράψτε όλες τις ρίζες που ανήκουν στο διάστημα \left(\frac(7\pi )2;\,\frac(9\pi )2\right].

Δείξε λύση

Λύση

ΕΝΑ)Επειδή \sin \frac\pi 3=\cos \frac\pi 6,Οτι \sin ^2\frac\pi 3=\cos ^2\frac\pi 6,Αυτό σημαίνει ότι η δεδομένη εξίσωση είναι ισοδύναμη με την εξίσωση \cos^2x=\cos ^22x, η οποία, με τη σειρά της, είναι ισοδύναμη με την εξίσωση \cos^2x-\cos ^2 2x=0.

Αλλά \cos ^2x-\cos ^22x= (\cos x-\cos 2x)\cdot (\cos x+\cos 2x)Και

\cos 2x=2 \cos ^2 x-1, οπότε η εξίσωση γίνεται

(\cos x-(2 \cos ^2 x-1))\,\cdot(\cos x+(2 \cos ^2 x-1))=0,

(2 \cos ^2 x-\cos x-1)\,\cdot (2 \cos ^2 x+\cos x-1)=0.

Τότε είτε 2 \cos ^2 x-\cos x-1=0, είτε 2 \cos ^2 x+\cos x-1=0.

Λύνοντας την πρώτη εξίσωση ως δευτεροβάθμια εξίσωση για το \cos x, παίρνουμε:

(\cos x)_(1,2)=\frac(1\pm\sqrt 9)4=\frac(1\pm3)4.Επομένως είτε \cos x=1 είτε \cos x=-\frac12.Αν \cos x=1, τότε x=2k\pi , k \in \mathbb Z. Αν \cos x=-\frac12,Οτι x=\pm \frac(2\pi )3+2s\pi, s \in \mathbb Z.

Ομοίως, λύνοντας τη δεύτερη εξίσωση, παίρνουμε είτε \cos x=-1 είτε \cos x=\frac12.Αν \cos x=-1, τότε οι ρίζες x=\pi +2m\pi , m \in \mathbb Z.Αν \cos x=\frac12,Οτι x=\pm \frac\pi 3+2n\pi , n \in \mathbb Z.

Ας συνδυάσουμε τις λύσεις που προέκυψαν:

x=m\pi , m \in \mathbb Z; x=\pm \frac\pi 3 +s\pi , s \in \mathbb Z.

σι)Ας επιλέξουμε τις ρίζες που εμπίπτουν σε ένα δεδομένο διάστημα χρησιμοποιώντας έναν κύκλο αριθμών.

Παίρνουμε: x_1 =\frac(11\pi )3, x_2=4\pi, x_3 =\frac(13\pi )3.

Απάντηση

ΕΝΑ) m\pi, m\in \mathbb Z; \pm \frac\pi 3 +s\pi , s \in \mathbb Z;

σι) \frac(11\pi )3, 4\pi, \frac(13\pi )3.

Πηγή: «Μαθηματικά. Προετοιμασία για την Ενιαία Κρατική Εξέταση 2017. Επίπεδο προφίλ." Εκδ. F. F. Lysenko, S. Yu. Kulabukhova.

Κατάσταση

ΕΝΑ)Λύστε την εξίσωση 10\cos ^2\frac x2=\frac(11+5ctg\left(\dfrac(3\pi )2-x\right) )(1+tgx).

σι)Να αναφέρετε τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα \left(-2\pi ; -\frac(3\pi)2\δεξιά).

Δείξε λύση

Λύση

ΕΝΑ) 1. Σύμφωνα με τον τύπο μείωσης, ctg\left(\frac(3\pi )2-x\right) =tgx.Το πεδίο ορισμού της εξίσωσης θα είναι τέτοιες τιμές του x τέτοιες ώστε \cos x \neq 0 και tan x \neq -1. Ας μετατρέψουμε την εξίσωση χρησιμοποιώντας τον τύπο συνημιτόνου διπλής γωνίας 2 \cos ^2 \frac x2=1+\cos x.Παίρνουμε την εξίσωση: 5(1+\cos x) =\frac(11+5tgx)(1+tgx).

σημειώσε ότι \frac(11+5tgx)(1+tgx)= \frac(5(1+tgx)+6)(1+tgx)= 5+\frac(6)(1+tgx),οπότε η εξίσωση γίνεται: 5+5 \cos x=5 +\frac(6)(1+tgx).Από εδώ \cos x =\frac(\dfrac65)(1+tgx), \cos x+\sin x =\frac65.

2. Μετασχηματίστε το \sin x+\cos x χρησιμοποιώντας τον τύπο αναγωγής και τον τύπο του αθροίσματος των συνημιτόνων: \sin x=\cos \left(\frac\pi 2-x\right), \cos x+\sin x= \cos x+\cos \left(\frac\pi 2-x\right)= 2\cos \frac\pi 4\cos \left(x-\frac\pi 4\right)= \sqrt 2\cos \left(x-\frac\pi 4\right) = \frac65.

Από εδώ \cos \left(x-\frac\pi 4\right) =\frac(3\sqrt 2)5.Που σημαίνει, x-\frac\pi 4= arc\cos \frac(3\sqrt 2)5+2\pi k, k \in \mathbb Z,

ή x-\frac\pi 4= -arc\cos \frac(3\sqrt 2)5+2\pi t, t \in \mathbb Z.

Να γιατί x=\frac\pi 4+arc\cos \frac(3\sqrt 2)5+2\pi k,k \in \mathbb Z,

ή x =\frac\pi 4-arc\cos \frac(3\sqrt 2)5+2\pi t,t \in \mathbb Z.

Οι τιμές του x που βρέθηκαν ανήκουν στον τομέα ορισμού.

σι)Ας μάθουμε πρώτα πού πέφτουν οι ρίζες της εξίσωσης σε k=0 και t=0. Αυτοί θα είναι αριθμοί ανάλογα a=\frac\pi 4+arccos \frac(3\sqrt 2)5Και b=\frac\pi 4-arccos \frac(3\sqrt 2)5.

1. Ας αποδείξουμε τη βοηθητική ανισότητα:

\frac(\sqrt 2)(2)<\frac{3\sqrt 2}2<1.

Πραγματικά, \frac(\sqrt 2)(2)=\frac(5\sqrt 2)(10)<\frac{6\sqrt2}{10}=\frac{3\sqrt2}{5}.

Σημειώστε επίσης ότι \left(\frac(3\sqrt 2)5\right) ^2=\frac(18)(25)<1^2=1, Που σημαίνει \frac(3\sqrt 2)5<1.

2. Από τις ανισότητες (1) Με την ιδιότητα συνημιτόνου τόξου παίρνουμε:

τόξο 1

Από εδώ \frac\pi 4+0<\frac\pi 4+arc\cos \frac{3\sqrt 2}5<\frac\pi 4+\frac\pi 4,

0<\frac\pi 4+arccos \frac{3\sqrt 2}5<\frac\pi 2,

Επίσης, -\frac\pi 4

0=\frac\pi 4-\frac\pi 4<\frac\pi 4-arccos \frac{3\sqrt 2}5< \frac\pi 4<\frac\pi 2,

Για k=-1 και t=-1 λαμβάνουμε τις ρίζες της εξίσωσης a-2\pi και b-2\pi.

\Bigg(a-2\pi =-\frac74\pi +arccos \frac(3\sqrt 2)5,\, b-2\pi =-\frac74\pi -arccos \frac(3\sqrt 2)5\Bigg).Εν -2\pi

2\pi Αυτό σημαίνει ότι αυτές οι ρίζες ανήκουν στο δεδομένο διάστημα \left(-2\pi , -\frac(3\pi )2\right).

Για άλλες τιμές των k και t, οι ρίζες της εξίσωσης δεν ανήκουν στο δεδομένο διάστημα.

Πράγματι, αν k\geqslant 1 και t\geqslant 1, τότε οι ρίζες είναι μεγαλύτερες από 2\pi. Αν k\leqslant -2 και t\leqslant -2, τότε οι ρίζες είναι μικρότερες -\frac(7\pi )2.

Απάντηση

ΕΝΑ) \frac\pi4\pm arccos\frac(3\sqrt2)5+2\pi k, k\in\mathbb Z;

σι) -\frac(7\pi)4\pm arccos\frac(3\sqrt2)5.

Πηγή: «Μαθηματικά. Προετοιμασία για την Ενιαία Κρατική Εξέταση 2017. Επίπεδο προφίλ." Εκδ. F. F. Lysenko, S. Yu. Kulabukhova.

Κατάσταση

ΕΝΑ)Λύστε την εξίσωση \sin \left(\frac\pi 2+x\right) =\sin (-2x).

σι)Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα ;

Δείξε λύση

Λύση

ΕΝΑ)Ας μετατρέψουμε την εξίσωση:

\cos x =-\sin 2x,

\cos x+2 \sin x \cos x=0,

\cos x(1+2 \sin x)=0,

\cos x=0,

x =\frac\pi 2+\pi n, n\in \mathbb Z;

1+2 \sin x=0,

\sin x=-\frac12,

x=(-1)^(k+1)\cdot \frac\pi 6+\pi k, k \in \mathbb Z.

σι)Βρίσκουμε τις ρίζες που ανήκουν στο τμήμα χρησιμοποιώντας τον μοναδιαίο κύκλο.

Το υποδεικνυόμενο διάστημα περιέχει έναν μόνο αριθμό \frac\pi 2.

Απάντηση

ΕΝΑ) \frac\pi 2+\pi n, n \in \mathbb Z; (-1)^(k+1)\cdot \frac\pi 6+\pi k, k \in \mathbb Z;

σι) \frac\pi 2.

Πηγή: «Μαθηματικά. Προετοιμασία για την Ενιαία Κρατική Εξέταση 2017. Επίπεδο προφίλ." Εκδ. F. F. Lysenko, S. Yu. Kulabukhova.

Κατάσταση

δεν περιλαμβάνεται στο DZ.

Που σημαίνει, \sin x \neq 1.

Διαιρέστε και τις δύο πλευρές της εξίσωσης με έναν παράγοντα (\sin x-1),διαφορετικό από το μηδέν. Παίρνουμε την εξίσωση \frac 1(1+\cos 2x)=\frac 1(1+\cos (\pi +x)),ή εξίσωση 1+\cos 2x=1+\cos (\pi +x).Εφαρμόζοντας τον τύπο αναγωγής στην αριστερή πλευρά και τον τύπο αναγωγής στα δεξιά, λαμβάνουμε την εξίσωση 2 \cos ^2 x=1-\cos x.Αυτή η εξίσωση είναι με αντικατάσταση \cos x=t,Οπου -1 \leqslant t \leqslant 1μειώστε το στο τετράγωνο: 2t^2+t-1=0,των οποίων οι ρίζες t_1=-1Και t_2=\frac12.Επιστρέφοντας στη μεταβλητή x, παίρνουμε \cos x = \frac12ή \cos x=-1,που x=\frac \pi 3+2\pi m, m\in \mathbb Z, x=-\frac \pi 3+2\pi n, n \in \mathbb Z, x=\pi +2\pi k, k \in \mathbb Z.

σι)Ας λύσουμε τις ανισότητες

1) -\frac(3\pi )2 \leqslant \frac(\pi )3+2\pi m \leqslant -\frac \pi 2,

2) -\frac(3\pi )2 \leqslant -\frac \pi 3+2\pi n \leqslant -\frac \pi (2,)

3) -\frac(3\pi )2 \leqslant \pi+2\pi k \leqslant -\frac \pi 2, Μ, n, k \in \mathbb Z.

1) -\frac(3\pi )2 \leqslant \frac(\pi )3+2\pi m \leqslant -\frac \pi 2, -\frac32\leqslant \frac13+2m \leqslant -\frac12 -\frac(11)6 \leqslant 2m\leqslant -\frac56, -\frac(11)(12) \leqslant m \leqslant -\frac5(12).

\αριστερά [-\frac(11)(12);-\frac5(12)\right].

2) -\frac (3\pi) 2 \leqslant -\frac(\pi )3+2\pi n \leqslant -\frac(\pi )(2), -\frac32 \leqslant -\frac13 +2n \leqslant -\frac12, -\frac76 \leqslant 2n \leqslant -\frac1(6), -\frac7(12) \leqslant n \leqslant -\frac1(12).

Δεν υπάρχουν ακέραιοι αριθμοί στην περιοχή \left[ -\frac7(12) ; -\frac1(12)\right].

3) -\frac(3\pi )2 \leqslant \pi +2\pi k\leqslant -\frac(\pi )2, -\frac32 \leqslant 1+2k\leqslant -\frac12, -\frac52 \leqslant 2k \leqslant -\frac32, -\frac54 \leqslant k \leqslant -\frac34.

Αυτή η ανισότητα ικανοποιείται από k=-1 και μετά x=-\pi.