Ранг на матрицата е важна нумеричка карактеристика. Најкарактеристична задача која бара наоѓање на ранг на матрицата е да го тестираат унифициран систем на линеарни алгебарски равенки. Во оваа статија ќе го дадеме концептот на одделението на матрицата и ќе ги разгледаме методите на неговиот престој. За подобро асимилација на материјалот, ги анализираме решенијата на неколку примери во детали.
Навигација страница.
Утврдување на одделението на матрицата и потребните дополнителни концепти.
Пред да ја избирате дефиницијата за одделението на матрицата, неопходно е добро да се справите со концептот на малолетник, а темелите на Marytrix подразбираат способност за пресметување на одредник. Значи, ние препорачуваме, доколку е потребно, да се потсетиме на теоријата на статијата методи за наоѓање на детерминанта на матрицата, својствата на детерминантот.
Земете ја матрицата со цел. Дозволете K да биде одреден природен број кој не го надминува најмалите од M и N броевите, односно ![]() .
.
Дефиниција.
Мала на К-ти ред Матрикс А се нарекува детерминанта на квадратна матрица на редот составен од елементите на матрицата А, кои однапред ги избрале колумните избрани жици и K колони, а локацијата на матричните елементи е зачувана.
Со други зборови, ако во матрицата и избришете (P-K) редови и (N-K) колони, и од преостанатите елементи за да се направи матрица, истовремено одржувајќи го уредувањето на елементите на матрицата А, тогаш детерминанта на Како резултат на матрицата е мала од редот k матрикс a.
Ние ќе разбереме со дефиницијата на малолетникот на матрицата на пример.
Размислете за матрицата  .
.
Ние пишуваме неколку малолетни лица од првиот ред на оваа матрица. На пример, ако ја избереме третата низа и втората колона на матрицата А, тогаш нашиот избор одговара на помалиот од првиот ред ![]() . Со други зборови, за добивање на ова малолетно лице, ги преминавме првите и втората реда, како и првите, трети и четврти столбови од Матрикс А, и од преостанатиот елемент беа детерминанта. Ако ја одберете првата низа и третата колона на матрицата А, тогаш ќе добиеме мали
. Со други зборови, за добивање на ова малолетно лице, ги преминавме првите и втората реда, како и првите, трети и четврти столбови од Матрикс А, и од преостанатиот елемент беа детерминанта. Ако ја одберете првата низа и третата колона на матрицата А, тогаш ќе добиеме мали ![]() .
.
Ние ја илустрираме постапката за добивање дискутирани малолетни лица од првиот ред  и.
и.  .
.
Така, рударите од првиот ред на матрицата се елементи на матрицата.
Да покажеме неколку малолетни лица од вториот поредок. Изберете две линии и две колони. На пример, земете ги првите и втората реда и третата и четвртата колона. Со овој избор имаме втор ред малолетник  . Ова малолетникот, исто така, може да биде вградено од матрицата и од третиот ред, првата и втората колона.
. Ова малолетникот, исто така, може да биде вградено од матрицата и од третиот ред, првата и втората колона.
Друг малолетник од вториот поредок на матрицата А е.
Ние ќе ја илустрираме изградбата на овие малолетни лица од вториот поредок  и.
и.  .
.
Малолетните од третиот ред на матрицата А може да се најдат слично. Бидејќи во матрицата и само три линии, тогаш изберете ги сите. Ако ги изберете трите први колони на овие редови, тогаш ќе добиеме малопродажен од третиот ред 
Исто така може да се изгради со преминување на последната колона од матрицата а.
Уште еден малолетник е трет ред 
Како резултат на преминувањето на третата колона на матрицата а.
Еве цртеж, покажувајќи изградба на овие малолетни лица од третиот ред  и.
и.  .
.
За оваа матрица, малолетникот на Редот над третиот не постои, бидејќи.
Колку малолетни лица од k-th цел матрица и ред?
Бројот на наредби со малолетници К може да се пресмета како, каде  и.
и.  - Бројот на комбинации од П од К и од Н од К, соодветно.
- Бројот на комбинации од П од К и од Н од К, соодветно.
Како да ги изградите сите малолетни лица за K Matrixa и цел P за n?
Потребни ни се различни броеви на жиците на Матрикс и многу броеви на колони. Снимајте сè комбинации од P елементи од К (Тие ќе кореспондираат со избраните редови на Матриксот А при изградба на помал редослед k). За секоја комбинација на броеви на ред, ние секвенцијално ги додаваме сите комбинации од n елементи од броеви на K колони. Овие групи на комбинации на линии и броеви на колоните на матриксните колони ќе помогнат да ги направат сите малолетни лица од редот k.
Ние ќе анализираме на пример.
Пример.
Најди ги сите малолетни лица од вториот ред на матрицата.
Одлука.
Бидејќи редоследот на изворната матрица е 3 до 3, вкупните малолетни лица од вториот поредок ќе бидат  .
.
Ги пишуваме сите комбинации од 3 2 броеви на линиите на матрицата А: 1, 2; 1, 3 и 2, 3. Сите комбинации од 3 во 2 колони броеви се 1, 2; 1, 3 и 2, 3.
Земете ги првите и вториот линии на матрицата а. Со изборот на првите и втората колона на овие редови, првите и третата колони, втората и третата колони, соодветно ќе ги примаме малолетниците. 
За првите и трети линии со сличен избор на колони имаме 
Останува за вториот и третиот реда додадете прва и втора, прва и трета, втора и трета колони: 
Значи, се наоѓаат сите девет малолетни лица од вториот поредок на матрицата.
Сега можете да одите на дефиницијата за одделението на матрицата.
Дефиниција.
Ранг Матрикс - Ова е највисок редослед на помали матрица, освен нула.
Ранг Матрикс А означува како ранг (А). Можете исто така да се сретнете со ознаките rg (а) или заѕвони (а).
Од дефинициите на одделението на Матрикс и Мала, матрицата може да заклучи дека прстенот на нултата матрица е нула, а ранг на матрицата не е помал од еден.
Наоѓање на одделение на матрица по дефиниција.
Значи, првиот метод за наоѓање на ранг на матрицата е метод на интерстицијален малкоров. Овој метод се заснова на одредување на одделението на матрицата.
Да треба да го најдеме ранг на матрицата и редот.
Накратко опишете алгоритам Решенија за овој проблем со начинот на мали сортирање.
Ако има барем еден елемент на матрицата, различен од нула, тогаш ранг на матрицата е барем еднаков на еден (бидејќи постои малолетник од првиот ред, а не еднаков на нула).
Следно, поминете низ малолетниците од вториот поредок. Ако сите малолетни лица од вториот поредок се нула, ранг Матриксот е еднаков на еден. Ако има барем една глупост малолетник од вториот поредок, тогаш се свртува кон третиот ред помало земање мостри, а крпа на матрицата е најмалку два.
Слично на тоа, ако сите малолетни лица од третиот ред се еднакви на нула, тогаш ранг на матрицата е два. Ако има најмалку еден малолетник од третиот редослед, освен нула, тогаш ранг на матрицата е најмалку три, а ние се скршиме на четвртиот ред зло.
Забележете дека прстенот на матрицата не може да го надмине најмалиот од броевите p и n.
Пример.
Пронајдете го ранг на матрицата  .
.
Одлука.
Бидејќи матрицата не е нула, тогаш нејзиниот ранг не е помал од еден.
Мала од втор ред  Поради тоа, различно од нула, ранг на матрицата не е помал од два. Ние се свртиме кон третиот ред помало земање мостри. Сите тие
Поради тоа, различно од нула, ранг на матрицата не е помал од два. Ние се свртиме кон третиот ред помало земање мостри. Сите тие  парчиња
парчиња 


Сите малолетни лица од третиот ред се нула. Затоа, ранг на матрицата е два.
Одговор:
Ранг (а) \u003d 2.
Наоѓање на одделение од матрица со методот на раздвижените малолетници.
Постојат и други методи за наоѓање на ранг на матрица кои ви дозволуваат да го добиете резултатот со помалку пресметковна операција.
Еден од овие методи е метод на раздвижените заинтересирани.
Кажете S. концептот на здодевен малолетник.
Се вели дека малолетникот М во ред (k + 1) налогот на матрицата се врзува помалиот М од налогот K матрикс А, ако матрицата што одговара на малолетникот М во ред, "содржи" матрица што одговара на малолетникот М.
Со други зборови, матрицата што одговара на граничниот малт M се добива од матрицата што одговара на граничи со малолетник М во ред, преминување на елементите на една линија и една колона.
На пример, размислете за матрицата  И земи го малолетното поредок. Ги пишуваме сите малолетни лица за фокусирање:
И земи го малолетното поредок. Ги пишуваме сите малолетни лица за фокусирање: 
Методот на фокусирање на малцинствата е оправдан од следната теорема (го даваме текстот без доказ).
Теорема.
Ако целото Министерство за економизирање на MATRIX и нарачката P за N е нула, тогаш сите малолетници од налогот (K + 1) матрица се нула.
Така, за да ја пронајдете одделението на матрицата, не е неопходно да ги средите сите малолетни лица, доволно исчезнување. Бројот на рудари, кој се фокусира на малолетник на редот на Матрикс и ред, е со формулата ![]() . Треба да се напомене дека на малолетници, кои го фокусираат малолетникот К-Т-ти редот на Матрикс А, не повеќе од послуќни (К + 1)-член на матрицата а. Затоа, во повеќето случаи, употребата на методот на раздвижените рудари е попрофитабилна за едноставноста на сите заинтересии.
. Треба да се напомене дека на малолетници, кои го фокусираат малолетникот К-Т-ти редот на Матрикс А, не повеќе од послуќни (К + 1)-член на матрицата а. Затоа, во повеќето случаи, употребата на методот на раздвижените рудари е попрофитабилна за едноставноста на сите заинтересии.
Да се \u200b\u200bсвртиме кон наоѓање на одделение на матрица со методот на раздвижените малолетници. Накратко опишете алгоритам на овој метод.
Ако матрицата не е нула, тогаш како рудар од првата нарачка земаме било кој елемент на матрицата, и други од нула. Ние ги сметаме за гранични малолетници. Ако тие се сите нула, тогаш прстенот на матрицата е еднаков на еден. Ако има барем еден ненуден обврзувачки малолетник (неговиот редослед е два), тогаш се свртуваме кон разгледување на своите обврзувачки малолетници. Ако тие се сите нула, тогаш ранг (а) \u003d 2. Ако барем еден обврзувачки малолетник е различен од нула (неговиот редослед е еднаков на три), тогаш ги разгледуваме неговите обврзувачки малолетници. Итн. Како резултат на тоа, ранг (А) \u003d k, ако сите малолетници за фокусирање (k + 1)--тата цел на матрицата се нула, или ранг (а) \u003d мин (P, N), ако има незначително малолетник, Врзување на помал редослед (мин (p, n) - 1).
Ние ќе го анализираме начинот на раздвижените малолетни лица за да ја пронајдеме одделението на матрицата на примерот.
Пример.
Пронајдете го ранг на матрицата  Методот на раздвижените малолетници.
Методот на раздвижените малолетници.
Одлука.
Бидејќи елементот А 1 1 матрица е различен од нула, ние ќе го земеме како министер за првиот ред. Да почнеме да бараме пограничен рудар освен нула: 
Фондацијата се наоѓа во втор ред, различен од нула. Со поместување на неговите гранични малолетници (нивни ![]() парчиња):
парчиња): 
Сите малолетни лица, кои фокусирајќи го малолетникот на вториот поредок се нула, затоа, ранг на матрицата А е два.
Одговор:
Ранг (а) \u003d 2.
Пример.
Пронајдете го ранг на матрицата  Со помош на малолетни лица.
Со помош на малолетни лица.
Одлука.
Како што е различно од нула, првиот ред ќе го земе елементот a 1 1 \u003d 1 матрица a. Обично го помали од вториот ред  Не е еднаква на нула. Ова малолетник е фокусирано на малолетник од третиот ред
Не е еднаква на нула. Ова малолетник е фокусирано на малолетник од третиот ред  . Бидејќи тоа не е еднакво на нула и не постои ниту еден лаење малолетник за него, тогаш ранг на матрицата А е еднаков на три.
. Бидејќи тоа не е еднакво на нула и не постои ниту еден лаење малолетник за него, тогаш ранг на матрицата А е еднаков на три.
Одговор:
Ранг (а) \u003d 3.
Наоѓање на ранг со користење на елементарни матрични трансформации (GAUS метод).
Размислете за друг начин да го пронајдете ранг на матрицата.
Следниве трансформации на матрицата се нарекуваат елементарни:
- пермутација на места на жици (или колони) на матрицата;
- множење на сите елементи од било кој ред (колона) на матрицата на произволен број k, различен од нула;
- додај во елементи од било кој ред (колона) на соодветните елементи на друга линија (колона) на матрицата помножена со произволен број k.
Матрикс Б се нарекува еквивалентна матрица аАко сте добиени од со користење на конечен број на елементарни трансформации. Еквивалентноста на матриците е означена со симболот "~", односно е напишано A ~ B.
Наоѓањето на одделението на матрица со користење на елементарните матрикс трансформации се базира на изјавата: ако матрицата се добиени од матрицата со користење на конечен број на елементарни трансформации, потоа ранг (A) \u003d ранг (B).
Валидноста на ова одобрение произлегува од својствата на детерминантот на матрицата:
- Кога ги измагнува рековвите (или колоните) на матрицата, нејзината детерминанта го менува знакот. Ако е нула, тогаш кога стринговите дозволуваат (колони) останува нула.
- Кога ги размножувате сите елементи на било кој ред (колона) на матрицата на произволен број k, различен од нула, детерминанта на добиената матрица е еднаква на детерминанта на почетната матрица помножена со K. Ако детерминанта на почетната матрица е нула, тогаш по множење на сите елементи од било кој ред или колона, детерминанта на добиената матрица, исто така, ќе биде нула.
- Дополнувањето на елементите на одредена линија (колона) на матрицата на соодветните елементи на друга линија (колона) на матрицата помножена со број К, не ја менува својата детерминанта.
Суштината на методот на елементарни трансформации Тоа е да се донесе матрица, чиј ранг треба да го најдеме, на трапезоидни (во одреден случај до врвот триаголен) користејќи елементарни трансформации.
За што е направено? Ранг на матрици од овој вид е многу лесно да се најде. Таа е еднаква на бројот на линии кои содржат најмалку еден ненулен елемент. И бидејќи ранг на матрицата за време на елементарните трансформации не се менува, добиената вредност ќе биде ранг на оригиналната матрица.
Да дадеме илустрации на матрици, од кои едната треба да излезе по трансформациите. Нивното гледиште зависи од редот на матрицата.

Овие илустрации се шаблони на кои ја претвораме матрицата а.
Ние опишуваме метод на алгоритам.
Дозволете ни да треба да го пронајдеме ранг на нејасни матрикс А од нарачката (P може да биде еднаков на n).
Значи ,. Умножете ги сите елементи на првиот ред на матрицата А. Во овој случај, ние добиваме еквивалентна матрица, ние го означуваме (1): 
На елементите на вториот ред на добиената матрица а (1) додадете соодветни елементи на првата линија множи со. На елементи на третата линија додадете соодветните елементи на првата линија множи со. И така натаму до P-тиот ред. Ние добиваме еквивалентна матрица, ние го означуваме (2): 
Ако сите елементи на добиената матрица, кои се во линии од втората од p-yu се нула, ранг на оваа матрица е еднаков на еден, и затоа, ранг на првичната матрица е еднаков на еден.
Ако има барем еден ненулен елемент во редот од вториот до П-I, потоа продолжи да врши трансформации. И ние дејствуваме апсолутно слично, но само со дел од матрицата означена на сликата (2) 
Ако, а потоа ги преуредите стрингот и (или) колоните на матрицата А (2), така што "новиот" елемент станува ненуреро.
Бројот r се нарекува прстен на матрицата А, ако:
1) во матрицата А е помал од редот, различен од нула;
2) Сите малолетни лица (R + 1) и повисоко, ако тие постојат се нула.
Инаку, ранг на матрицата е највисок редослед на мали, различни од нула.
Ознаки: Ранга, r А или Р.
Од дефиницијата следи дека R е цел број позитивен број. За нула матрици, ранг се смета за нула.
Назначување на услуга. Онлајн калкулатор е дизајниран да се најде ранг Матрикс. Во овој случај, решението е зачувано во формат на Word и Excel. Видете Пример решение.
Инструкции. Изберете ја димензијата на матрицата, кликнете Next.
Дефиниција. Нека му биде дадена матрица р. Секоја помала матрица, различна од нула и со цел R, се нарекува основни, а линиите и колоните на неговите компоненти се основни жици и колони.
Според оваа дефиниција, матрицата А може да има неколку основни малолетници.
Ранг на една матрица e е n (бројот на жици).
Пример 1. Се дадени две матрици,  И нивната малолетник
И нивната малолетник  ,
,  . Кој може да се земе како основен?
. Кој може да се земе како основен?
Одлука. Мала М 1 \u003d 0, така што не може да биде основно за било која од матриците. Мала М 2 \u003d -9 ≠ 0 и има ред 2, што значи дека може да се земе како основни матрици А или / и Б, под услов тие да имаат рангирани еднакви на 2. Од detb \u003d 0 (како детерминанта со две пропорционални колони), тогаш rangb \u003d 2 и m 2 може да се земе за базната помала матрица Б. Ранг на матрицата А е 3, поради фактот дека deta \u003d -27 ≠ 0 И, според тоа, нарачајте го базниот малолетник од оваа матрица треба да биде 3, односно M2 не е основно за матрицата a. Забележете дека матрицата А е единствената база еднаква на детерминантот на матрицата а.
Теорема (врз основа на малолетник).
Секоја низа (колона) на матрицата е линеарна комбинација на нејзините основни жици (колони).
Последици од теоремата.
- Сите (R + 1) колони (линии) на Rank Matrix r линеарно зависна.
- Ако партанот на матрицата е помала од бројот на своите редови (колони), тогаш нејзините линии (колони) се линеарно зависни. Ако Ranga е еднаков на бројот на своите редови (колони), тогаш линиите (колоните) се линеарно независни.
- Детерминантата на матрицата А е нула ако и само ако нејзините линии (колони) се линеарно зависни.
- Ако додадете друга линија до Strix String (колона), (колона) се множи на било кој број освен нула, тогаш прстенот на матрицата нема да се промени.
- Ако во матрицата, преминете ја низата (колона), што е линеарна комбинација на други линии (колони), тогаш одделението на матрицата нема да се промени.
- Ранг на матрицата е еднаков на максималниот број на нејзините линеански независни линии (колони).
- Максималниот број на линеански независни линии се совпаѓа со максималниот број на линеански независни колони.
Пример 2. Најди ранг Матрикс  .
.
Одлука.
Врз основа на дефиницијата на одделението на матрицата, ние ќе бараме малолетник од највисок редослед, освен нула. Прво ја трансформираме матрицата во поедноставна форма. За да го направите ова, првата низа на матрица се размножува на (-2) и додадете во втората, тогаш тоа ќе се размножува на (-1) и ќе додадете на третото место.
Дефиниција. Ранг Матрикс Се нарекува максималниот број на линеарно независни линии како вектори.
Теорема 1 на ранг на матрицата. Ранг Матрикс Се нарекува максимален редослед на матрицата различна од нула.
Ние веќе го расклопивме концептот на малолетник во лекцијата за идентификатори, а сега го генерализираме. Земете некои редови во матрицата и колку колони, и ова "колку" треба да биде помал од бројот на редови и мртрикс, и за стрингови и колони тоа "колку" треба да биде ист број. Потоа, на пресекот колку редови и колку колони ќе бидат помали матрицата од нашата првична матрица. Детерминантата е матрици и ќе има малолетник на К-ти ред, ако "колку" споменати "(број на редови и колони) го означуваат К.
Дефиниција.Мала ( р.+1) -О-ред во кој избраните помали лаги р.- Редот, наречен, се нарекува граници за ова малолетно лице.
Најчесто се користат два начина наоѓање на ранг Матрикс. тоа метод на Busty Translors и. метод на елементарни трансформации (GAUS метод).
Со начинот на фокусирање на малолетници, се користи следнава теорема.
Теорема 2 на ранг на матрицата.Ако малолетникот може да се направи од матричните елементи р.- цел, не е еднаков на нула, тогаш ранг на матрицата е еднаков р..
Со методот на елементарни трансформации, се користи следниот имот:
Ако трапезоидна матрица се добиени со елементарни трансформации, што е еквивалентно на изворот, тогаш ранг на оваа матрица Тоа е бројот на редови во него, освен жиците кои се состојат од нули.
Воведување на одделение на матрица со методот на раздвижените малолетници
Досадното малолетник се нарекува малолетник со поголем редослед во врска со ова, ако овој помал редослед го содржи овој малолетник сам по себе.
На пример, со оглед на матрицата
Земете мало.
овие малолетници ќе се градат:
Алгоритам за наоѓање на матрица од одделение Следно.
1. Ние не наоѓаме еднаква нула на малолетници од вториот поредок. Ако сите малолетни лица од вториот редослед се еднакви на нула, ранг на матрицата ќе биде еднаков на еден ( р. =1 ).
2. Ако има најмалку еден втор ред мало, не е еднакво на нула, тогаш ние ги сочинуваме малолетникот на третиот ред. Ако сите малолетни лица од третиот ред се нула, тогаш крпа на матрицата е две ( р. =2 ).
3. Ако барем еден од вртењето на малолетни лица од третиот ред не е нула, тогаш ги сочинуваме основните малолетници. Ако сите плодни малолетници од четвртиот ред се нула, тогаш крпа на матрицата е три ( р. =2 ).
4. Продолжуваме се додека големината на матрицата дозволува.
Пример 1. Најди ранг Матрикс
 .
.
Одлука. Мала од втор ред ![]() .
.
Исклучи го. Четириесет фондови ќе бидат четири:
 ,
,
 ,
,
Така, сите финансиски малолетници од третиот ред се нула, затоа, ранг на оваа матрица е два ( р. =2 ).
Пример 2. Најди ранг Матрикс
Одлука. Ранг на оваа матрица е 1, бидејќи сите малолетни лица од вториот редослед на оваа матрица се еднакви на нула (во ова, како и во случаите на средства во два следниве примери, скапи студенти се поканети да бидат убедени независно, можеби Користење на правилата за пресметување на детерминанти), и меѓу малолетниците на првиот ред, односно меѓу елементите на матрицата, не постојат еднакви нула.
Пример 3. Најди ранг Матрикс
Одлука. Мала од вториот поредок на оваа матрица, во сите малолетници од третиот ред на оваа матрица се нула. Како резултат на тоа, ранг на оваа матрица е два.
Пример 4. Најди ранг Матрикс
Одлука. Ранг на оваа матрица е 3, бидејќи единствениот малолетник од третиот ред на оваа матрица е 3.
Воведување на ранг на матрицата со методот на елементарни трансформации (GAUS метод)
Веќе во примерот 1, може да се види дека задачата за одредување на одделението на матрицата со методот на раздвижените мали потреби за пресметување на голем број на детерминанти. Меѓутоа, постои начин да се намали обемот на компјутери на минимум. Овој метод се базира на употребата на елементарни трансформации на матрици и исто така се нарекува GAUS метод.
Според елементарните трансформации на матрицата се следните операции:
1) множење на било која низа или било која колона од матрица со број освен нула;
2) додавање на елементи од било која низа или било која колона од матрицата на соодветните елементи на друга линија или колона помножено со ист број;
3) промена на местата на два реда или колони на матрицата;
4) отстранување на "нула" жици, тоа е, како што сите елементи од кои се нула;
5) отстранување на сите пропорционални линии освен еден.
Теорема.Во случај на елементарна трансформација, ранг на матрицата не се менува. Со други зборови, ако сме елементарни трансформации од матрицата A. Префрлен на матрицата Б. Потоа.
Дозволете да се постави некоја матрица:
 .
.
Означете во оваа матрица  произволни стрингови I.
произволни стрингови I.  арбитрарни колони
арбитрарни колони  . Потоа детерминанта
. Потоа детерминанта  -О ред составен од елементите на матрицата
-О ред составен од елементите на матрицата  Се наоѓа на пресекот на означени линии и колони се нарекува малолетник
Се наоѓа на пресекот на означени линии и колони се нарекува малолетник  -О со цел матрица
-О со цел матрица  .
.
Дефиниција 1.13.Ранг Матрикс  тоа се нарекува најголем поредок на малолетник на оваа матрица, различен од нула.
тоа се нарекува најголем поредок на малолетник на оваа матрица, различен од нула.
За да се пресмета одделението на матрицата, сите негови малолетни лица од најмалата нарачка треба да се разгледаат и, доколку барем еден од нив е различен од нула, преминете на разгледувањето на малолетникот на високиот ред. Овој пристап за одредување на одделението на матрица се нарекува метод (или метод на раздвижени мали).
Задача 1.4.Методот на раздвижените малолетници за одредување на ранг на матрицата  .
.
 .
.
Размислете за првите редови на првиот ред, на пример,  . Потоа се свртуваме кон разгледување на некои конвекции од втор ред.
. Потоа се свртуваме кон разгледување на некои конвекции од втор ред.
На пример,  .
.
Конечно, ние ги анализираме првите редови на третиот ред.
 .
.
Така, највисок редослед на мали, различни од нула, е 2, според тоа,  .
.
При решавањето на проблемот 1.4, може да се забележи дека бројот на малолетни средства за врзување на вториот ред се разликува од нула. Во овој поглед, се одвива следниов концепт.
Дефиниција 1.14.Основниот малолетник на матрицата се нарекува било, различно од нула малолетник, чиј редослед е еднаков на маргината на матрицата.
Теорема 1.2.(Теорема врз основа на мало). Основи линии (основни колони) се линеарно независни.
Забележете дека линиите (колоните) на матрицата се линеарно зависни ако и само ако барем еден од нив може да биде претставена како линеарна комбинација на преостанатите.
Теорема 1.3.Бројот на линеарно независни линии на матрицата е еднаков на бројот на линеарно независни колони на матрицата и еднаков на крилјата на матрицата.
Теорема 1.4.(Неопходна и доволна застапна за еднаквост нулта детерминанта). Со цел да се утврди  со цел
со цел  тоа беше еднакво на нула, потребно е и доволно што нејзините линии (колони) се линеарно зависни.
тоа беше еднакво на нула, потребно е и доволно што нејзините линии (колони) се линеарно зависни.
Пресметката на одделението на матрицата врз основа на употребата на неговата дефиниција е премногу незгодна операција. Ова станува неопходно за матрици со висока нарачка. Во овој поглед, во пракса, партарот на матрицата се пресметува врз основа на користење на теоремите 10.2 - 10.4, како и користење на концептите за еквивалентност на матрици и елементарни трансформации.
Дефиниција 1.15.Две матрици  и.
и.  се нарекуваат еквивалентни ако нивните редови се еднакви, т.е.
се нарекуваат еквивалентни ако нивните редови се еднакви, т.е.  .
.
Ако матрицата  и.
и.  еквивалент, потоа прослават
еквивалент, потоа прослават 
 .
.
Теорема 1.5.Ранг на матрицата не се менува од елементарните трансформации.
Ние ќе ги повикаме елементарните трансформации на матрицата  било која од следниве постапки на матрицата:
било која од следниве постапки на матрицата:
Заменете ја низата по колони и колони со соодветни линии;
Пермутација на линии на матрицата;
Изразувајќи ја низата, чии елементи се нула;
Множење на било која низа со број освен нула;
Додавањето на елементите на една линија на соодветните елементи на друга линија се множи на истиот број  .
.
Последица на теорема 1.5.Ако матрицата  добиени од матрицата
добиени од матрицата  со помош на конечен број на елементарни трансформации, тогаш матрицата
со помош на конечен број на елементарни трансформации, тогаш матрицата  и.
и.  еквивалент.
еквивалент.
При пресметувањето на одделението на матрицата, треба да се донесе со конечен број на елементарни трансформации во трапезоидна форма.
Дефиниција 1.16.Трапезоидни ќе се нарекуваат таква форма на застапеност на матрицата, кога во границата помалиот поредок различен од нула, сите елементи кои се под дијагонала се применуваат на нула. На пример:
 .
.

Овде  , елементи на матрицата
, елементи на матрицата  се применуваат на нула. Тогаш формата на застапеноста на таквата матрица ќе биде трапезоидна.
се применуваат на нула. Тогаш формата на застапеноста на таквата матрица ќе биде трапезоидна.
Како по правило, матриците на трапезоидната форма се даваат со помош на алгоритмот Гаус. Идејата за алгоритмот Гаус е дека, множење на елементите на првиот ред на матрицата до соодветните мултипликатори, ги бараат сите елементи на првата колона под елементот.  , ќе се претвори во нула. Потоа, множењето на елементите на втората колона до соодветните мултипликатори, ги бараат сите елементи на втората колона под елементот.
, ќе се претвори во нула. Потоа, множењето на елементите на втората колона до соодветните мултипликатори, ги бараат сите елементи на втората колона под елементот.  , ќе се претвори во нула. Следно пристигне на ист начин.
, ќе се претвори во нула. Следно пристигне на ист начин.
Задача 1.5.Определете го ранг на матрицата со информации до трапезоидната форма.
 .
.
За погодност за примена на AlgorithM Gauss, можете да ги замените првите и третите линии.





 .
.
Очигледно тука тука  . Сепак, за да го донесете резултатот до повеќе елегантна форма, можете дополнително да продолжите конвертирање преку колоните.
. Сепак, за да го донесете резултатот до повеќе елегантна форма, можете дополнително да продолжите конвертирање преку колоните.







 .
.
И, исто така, разгледајте важна практична тема за апликација: студија за систем на линеарни равенки за компатибилност.
Кој е ранг на матрицата?
Хумористичниот епиграф на статијата содржи голем дел од вистината. Зборот "ранг" самиот е обично поврзан со некоја хиерархија, најчесто, со скали на услуги. Колку е поголемо човечкото знаење, искуство, способности, бел престој итн. - Колку е поголема неговата позиција и опсегот на можности. Јас сум изразен од страна на младите, под ранг подразбира општ степен на "стрмништво".
И нашите математички браќа живеат според истите принципи. Јас ќе донесам некои произволни за прошетка нулта матрици:
Размислете дали во матрицата некои нулиЗа кој ранг можеме да зборуваме? Секој е запознаен со неформалниот израз "целосна нула". Во општеството, матриците се исти:
Рангирана нула матрицасекоја големина е нула.
Забелешка : Нулта матрица е означена со грчкото писмо "Тета"
Со цел подобро да го разберат ранг на матрицата тука, а потоа ќе привлечам материјали за спасување аналитичка геометрија. Размислете за нула вектор нашиот тродимензионален простор кој не специфицира одредена насока и е бескорисна за изградба афината база. Од алгебарска гледна точка, координатите на овој вектор се евидентираат матрикс "Еден до три" и логично (во наведената геометриска смисла) Неопходно е ранг на оваа матрица да е нула.
Сега размислете за неколку nenulevoy. колони вектори и. вектори стринг:
Во секоја инстанца има најмалку еден ненулен елемент, и ова е веќе нешто!
Ранг на било која не-нула векторска низа (вектор на колона) е еднаков на еден
И општо земено - ако во матрицата произволни големини Постојат најмалку еден ненулен елемент, а потоа нејзиниот ранг не помалку Единици.
Алгебарски векторски жици и вектори на колоните се апстрактно апстрактни, па ние ќе се вратиме назад во геометриската асоцијација. Nenuleva. вектор Одредува сосема дефинирана насока во вселената и е погодна за изградба. основаЗатоа, ранг на матрицата ќе се смета за еднаква единица.
Теоретски сертификат : Во линеарна алгебра, вектор е елемент на векторски простор (дефиниран преку 8 аксиоми), кој, особено, може да биде нарачана низа (или колона) на важечки броеви со додатоци дефинирани за нив и множење со валиден број . Повеќе информации за векторите може да се најдат во статијата. Линеарни трансформации.
линеарно зависна (изразени едни во други). Од геометриска гледна точка, координатите на Колинеарниот вектор се евидентираат во втората низа. ![]() кој не го унапреди случајот во зградата тридимензионална базаДа се \u200b\u200bбиде вишок во оваа смисла. Така, ранг на оваа матрица е исто така еднаков на еден.
кој не го унапреди случајот во зградата тридимензионална базаДа се \u200b\u200bбиде вишок во оваа смисла. Така, ранг на оваа матрица е исто така еднаков на еден.
Ги препишуваме координатите на векторите во колоните ( транспонирање на матрицата):
Што се променило од гледна точка на ранг? Ништо. Колоните се пропорционални, тоа значи дека ранг е еднаков на еден. Патем, забележете дека сите три линии се исто така пропорционални. Тие можат да бидат идентификувани со координати три Колинеарски авионски вектори од кои само еден Тоа е корисно за изградба на "рамна" база. И ова е целосно во согласност со нашата геометриска смисла на ранг.
Горенаведениот пример следи важна изјава:
Ранг на матрицата на редови е еднаков на оценките на колоните. Јас веќе го спомнав ова малку на лекцијата за ефективни методи за пресметување на одредник.
Забелешка : Од линеарна зависност на жиците следи линеарна зависност на колоните (и обратно). Но, со цел да заштедите време, и поради навиката, речиси секогаш ќе зборувам за линеарна зависност на линиите.
Продолжете да го обучувате нашето омилено милениче. Додадете во матрицата на координата на третата линија на друг Колитини вектор ![]() :
:
Дали тој помогнал во изградбата на тридимензионална основа? Се разбира не. Сите три векторски прошетки таму и тука на една песна, а ранг на матрицата е еднаква на еден. Можете да земете колку колективни вектори, велат, 100, ги ставаат своите координати во "сто по една" матрица и ранг на таков облакодер, сепак ќе останат единствен.
Се запознаат со матрицата чии жици линеарно независно. Еден пар нелилин вектори е погоден за градење на три-димензионална база. Ранг на оваа матрица е два.
И што е ранг на матрицата? Редовите се чини дека не се пропорционални ..., тоа значи, во идејата за три. Сепак, ранг на оваа матрица е исто така еднаков на два. Ги преклопував првите две линии и го снимив резултатот подолу, тоа е линеарно изразено Трета линија преку првите две. Геометриски матриксните жици одговараат на три координати компании векториРабота во овој троен има пар нелилин другари.
Како што можеш да видиш линеарна зависност Во разгледуваната матрица не е очигледно, и денес ние само ќе научиме да го повлечеме "на чиста вода".
Мислам дека многумина се погодени што е ранг на матрицата!
Размислете за матрица чии жици линеарно независно. Образец на вектори афината основа, а ранг на оваа матрица е три.
Како што знаете, секој четврти, петти, десетти вектор на тродимензионален простор ќе биде линеарно изразен преку основни вектори. Затоа, ако додадете било кој број на линии во матрицата, тогаш нејзиниот ранг сепак ќе биде три.
Слични аргументи може да се вршат за големи разни матрици (јасни, без геометриско значење).
Дефиниција : ранг на матрицата е максималниот број на линеарно независни линии. Или: ранг на матрицата е максималниот број на линеарни независни колони. Да, нивниот број секогаш се совпаѓа.
Од горенаведеното, исто така е важен практичен обележје: ранг на матрицата не ја надминува својата минимална димензија. На пример, во матрицата  четири линии и пет колони. Минималната димензија е четири, затоа, ранг на оваа матрица не надминува 4.
четири линии и пет колони. Минималната димензија е четири, затоа, ранг на оваа матрица не надминува 4.
Ознаки: Во светската теорија и пракса не постои општо прифатен стандард за означување на одделението на матрицата, најчесто може да се сретнете: - Како што велат, Англичанецот пишува еден, германски друг. Затоа, ајде до познатиот анегдота за американскиот и рускиот пекол за да го назначи ранг на матрицата од страна на мајчин збор. На пример :. И ако "неименуваната" матрица, која е пронајдена многу, тогаш можете само да запишете.
Како да го пронајдете ранг на матрицата со помош на менаџери?
Ако бабата имаше петта колона во матрицата, тогаш еден ќе дознае уште една четвртина наредба ("сина", "малина" + 5-та колона).
Излез: Максималниот поредок на нежни помали е три, тоа значи тоа.
Можеби не сите до крај беше сфатена со оваа фраза: малолетник од 4-тата цел е нула, но меѓу малолетниците на 3-то наредба беше пронајден нула - затоа максималниот редослед не-нула Мали и еднакви на три.
Се поставува прашањето, и зошто веднаш да ја пресметате детерминант? Па, прво, во повеќето задачи, матрицата не е квадратна, но второ, дури и ако имате не-нула вредност, задачата со голема веројатност извади, бидејќи тоа обично подразбира стандард "дното нагоре" решение. И во разгледуваниот пример, нултата детерминанта на 4-тата цел и целосно сугерира дека крпа на матрицата е само помалку од четири.
Морам да признаам, расклопната задача што ја донесов со себе за подобро да го објаснам методот на раздвижените малолетници. Во вистинска пракса, сè е полесно:
Пример 2.
Пронајдете го партанот на матрицата со методот на раздвижените малолетници 
Решение и одговор на крајот на лекцијата.
Кога алгоритмот работи побрзо? Ајде да се вратиме на истата "четири четири" матрица  . Очигледно, одлуката ќе биде најкратката во случај на "добро" аголни заинтересирани:
. Очигледно, одлуката ќе биде најкратката во случај на "добро" аголни заинтересирани:
И, ако, поинаку -.
Одразот воопшто не е хипотетички - постојат многу примери каде сè е ограничено само од аголни рудари.
Сепак, во некои случаи, уште еден метод е поефикасен:
Како да го најдете ранг на матрица со помош на Gauss метод?
Став е наменет за читателите кои веќе се запознаени со од Гаус И малку рака на неа.
Од техничка гледна точка, методот не се одликува со новина:
1) Со помош на елементарни трансформации, ја даваме матрицата до типот на чекор;
2) Парта на матрица е еднаква на бројот на редови.
Јасно е дека користењето на методот GAUS не го менува одделението на матрицата, а суштината тука е исклучително едноставна: според алгоритмот, за време на елементарните трансформации, сите екстра пропорционални (линеарно зависни) линии се откриени и отстранети, како резултат на што останува "сувиот остаток" - максималниот број на линеарно Независни линии.
Ние трансформираме стара позната матрица со координати на три колекторски вектори: 
(1) Втората линија додаде првата низа множи со -2. На третата линија додаде првата линија.
(2) нула стрингови отстранува.
Така, една линија остана, според тоа. Што да се каже е многу побрзо од пресметувањето на девет нулти малолетни лица од вториот налог и само тогаш заклучи.
Ве потсетувам дека само по себе алгебарска матрица Невозможно е да се промени ништо, а трансформациите се изведуваат само со цел да се разјасни ранг! Патем, ајде да престанеме повторно на прашањето, зошто да не? Извор матрица.  Носи информации кои се фундаментално различни од информациите на матрицата и стрингот. Во некои математички модели (без претерување), разликата во еден број може да биде прашање на живот и смрт. ... Се сетив на училишните наставници по математиката на основните и средните класи, кои безмилосно ја прекинаа проценката за 1-2 поени за најмала неточност или отстапување од алгоритмот. И тоа беше ужасно навреда кога, наместо тоа, се чини дека ќе се гарантира "пет", "добро" или полошо. Разбирањето дојде многу подоцна - и како е поинаку, да ги довери личноста сателити, нуклеарни боеви глави и електрани? Но, не се грижиш, јас не работам во овие области \u003d)
Носи информации кои се фундаментално различни од информациите на матрицата и стрингот. Во некои математички модели (без претерување), разликата во еден број може да биде прашање на живот и смрт. ... Се сетив на училишните наставници по математиката на основните и средните класи, кои безмилосно ја прекинаа проценката за 1-2 поени за најмала неточност или отстапување од алгоритмот. И тоа беше ужасно навреда кога, наместо тоа, се чини дека ќе се гарантира "пет", "добро" или полошо. Разбирањето дојде многу подоцна - и како е поинаку, да ги довери личноста сателити, нуклеарни боеви глави и електрани? Но, не се грижиш, јас не работам во овие области \u003d)
Дозволете ни да се свртиме кон повеќе информативни задачи каде што, меѓу другото, ќе се запознаеме со важни пресметковни техники. гаус Метод:
Пример 3.
Пронајдете го ранг на матрица користејќи елементарни трансформации 
Одлука: Дана Матрикс "Четири пет", што значи дека нејзиниот ранг е очигледно не повеќе од 4.
Во првата колона, нема 1 или -1, затоа се потребни дополнителни чекори за да се добијат најмалку една единица. Во цело време на страницата, постојано поставував прашање: "Дали е можно да ги преуредите колоните за време на елементарните трансформации?". Тука - преуредена првата втора колона, и сè е во ред! Во повеќето задачи каде што се користи гаус Метод, колоните навистина можат да ги преуредат. Но, нема потреба. И поентата не е дури ни во можна конфузија со променливи, факт е дека во класичниот курс на обука на повисока математика, оваа акција традиционално не се разгледува, па затоа ќе биде многу криво на таква брзина (а потоа тоа ќе биде принудени сè).
Втората точка се однесува на броевите. За време на одлуката е корисно да се води од следниве емпириски правила: елементарните трансформации може да се намалат со броевите на матрикс ако е можно.. На крајот на краиштата, со единица-две-три, многу е полесно да се работи многу полесно отколку, на пример, од 23, 45 и 97. и првата акција е насочена не само за да се добие единица во првата колона, туку и до елиминација на броеви 7 и 11.
Прво комплетно решение, потоа коментари: 
(1) Втората линија додаде првата низа множи со -2. На третата линија додаде првата низа помножена со -3. И на грамада: 1-ви линија беше додадена на 4-та линија множи со -1.
(2) Последните три линии се пропорционални. Отстранети 3 и 4 линии, втората линија се пресели на прво место.
(3) Втората линија додаде првата низа множи со -3.
Во дво-линиската матрица дадена на сцената.
Одговор:
Сега вашиот ред е да ги мачи четири-четири матрица:
Пример 4.
Најди ги матрицата заѕвони од Гаус 
Го потсетувам тоа гаус Метод Не претпоставува недвосмислена ригидност, а вашата одлука најверојатно ќе биде различна од мојата одлука. Кратка задача за дизајн на примерокот на крајот на лекцијата.
Кој метод да се користи за да ја пронајдете одделението на матрицата?
Во пракса, често не се вели во кој метод мора да се користи за да се најде ранг. Во таква ситуација, состојбата треба да се анализира - за некои матрици, порационално е да се спроведе решение преку малолетниците, а за другите е значително попрофитабилно да се применат елементарни трансформации:
Пример 5.
Најди ранг Матрикс 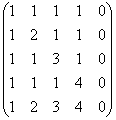
Одлука: Првиот начин некако исчезнува \u003d)
Само погоре, јас советував да не ги допрам колоните на матрицата, но кога има нулта колона, или пропорционални / совпаѓање колони, тогаш сеуште вреди да се спроведе ампутација: 
(1) Петтата нула колона, отстранете ја од матрицата. Така, ранг на матрицата не е повеќе од четири. Првата линија беше помножена со -1. Ова е уште еден брендиран GAUS метод, кој го претвора следниов ефект во пријатна прошетка:
(2) на сите редови, почнувајќи од вториот, додаде првиот стринг.
(3) Првата линија беше помножена со -1, третата линија беше поделена на 2, четвртата линија беше поделена на 3. до петтата линија додаде вториот низа множи со -1.
(4) До петтата линија додаде третата линија множи со -2.
(5) Последните две линии се пропорционални со петтата отстранета.
Како резултат на тоа, се добиени 4 линии.
Одговор:
Стандардна пет-приказна за самостојно учење:
Пример 6.
Најди ранг Матрикс
Кратко решение и одговор на крајот на лекцијата.
Треба да се напомене дека фразата "ранг на матрицата" нема толку често да се сретне во пракса, и во повеќето задачи што можете да ги направите без него. Но, постои една задача каде што концептот што се разгледува е главната личност, а во склучувањето на статијата ќе ја разгледаме оваа практична примена:
Како да се испита систем на линеарни равенки за единици?
Често, покрај решението системи на линеарни равенки Со состојба, тоа е претходно испитување во единици, односно да се докаже дека воопшто постои одлука. Клучна улога во таквите инспекциски претстави капера Капера теоремаЈас формулирам во потребната форма:
Ако ранг системски матрици еднаква на заѕвони проширен систем Матрикс, тогаш системот е координиран, и ако овој број се совпаѓа со бројот на непознати, тогаш решението е уникатно.
Така, за да го проучите системот за компатибилност, треба да ја проверите еднаквоста ![]() каде - систем Матрикс (сетете се на терминологијата од лекцијата Гаус Метод), но - проширен систем Матрикс (I.e. Matrix со коефициенти со променливи + колона на слободни членови).
каде - систем Матрикс (сетете се на терминологијата од лекцијата Гаус Метод), но - проширен систем Матрикс (I.e. Matrix со коефициенти со променливи + колона на слободни членови).