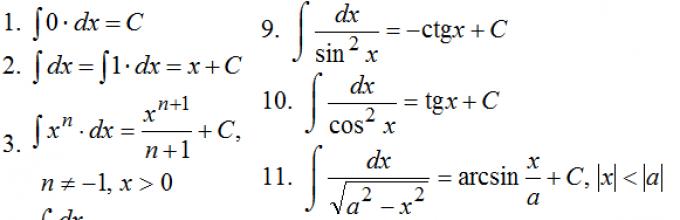Ниже перечислены четыре основных метода интегрирования.
1)
Правило интегрирования суммы или разности.
.
Здесь и далее u, v, w
- функции от переменной интегрирования x
.
2)
Вынесение постоянной за знак интеграла.
Пусть c
- постоянная, не зависящая от x
.
Тогда ее можно вынести за знак интеграла.
3)
Метод замены переменной.
Рассмотрим неопределенный интеграл .
Если удастся подобрать такую функцию φ(x)
от x
,
так что
,
то, выполнив замену переменной t = φ(x)
,
имеем
.
4)
Формула интегрирования по частям.
,
где u
и v
- это функции от переменной интегрирования.
Конечная цель вычисления неопределенных интегралов - это, путем преобразований, привести заданный интеграл к простейшим интегралам, которые называются табличными. Табличные интегралы выражаются через элементарные функции по известным формулам.
См. Таблица интегралов >>>
Пример
Вычислить неопределенный интеграл
Решение
Замечаем, что подынтегральная функция является суммой и разностью трех членов:
,
и .
Применяем метод 1
.
Далее замечаем, что подынтегральные функции новых интегралов умножены на постоянные 5, 4,
и 2
,
соответственно. Применяем метод 2
.
В таблице интегралов находим формулу
.
Полагая n = 2
,
находим первый интеграл.
Перепишем второй интеграл в виде
.
Замечаем, что .
Тогда
Применяем третий метод. Делаем замену переменной t = φ(x) = ln
x
.
.
В таблице интегралов находим формулу
Поскольку переменная интегрирования может обозначаться любой буквой, то
Перепишем третий интеграл в виде
.
Применяем формулу интегрирования по частям.
Положим .
Тогда
;
;
;
;
.
Окончательно имеем
.
Соберем члены с x 3
.
.
Ответ
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Интегрирование - это одна из основных операций в матанализе. Таблицы известных первообразных могут быть полезны, но сейчас они, после появления систем компьютерной алгебры, теряют свою значимость. Ниже находится список больше всего встречающихся первообразных.
Таблица основных интегралов
Другой, компактный вариант

Таблица интегралов от тригонометрических функций
От рациональных функций
От иррациональных функций
Интегралы от трансцендентных функций

"C" – произвольная константа интегрирования, которая определяется, если известно значение интеграла в какой-либо точке. Каждая функция имеет бесконечное число первообразных.
У большинства школьников и студентов бывают проблемы с вычислением интегралов. На этой странице собраны таблицы интегралов от тригонометрических, рациональных, иррациональных и трансцендентных функций, которые помогут в решении. Еще вам поможет таблица производных .
Видео - как находить интегралы
Если вам не совсем понятна данная тема, посмотрите видео, в котором всё подробно объясняется.Таблица первообразных
Используя свойства неопределенных интегралов и таблицу основных интегралов,
можно интегрировать некоторые функции.
ПРИЁМЫ ИНТЕГРИРОВАНИЯ
Метод подстановки
Наиболее общим приёмом интегрирования функций является метод
подстановки, который применяется тогда, когда искомый интеграл
является табличным, но путем ряда элементарных преобразований он может быть
сведен к табличному.
переменную.т заменяют переменной / по формуле х=φ(t) и,
следовательно, dx произведением φ"(t)dt.
Интегрирование по частям
Пример: необходимо найти интеграл
Здесь в двойные вертикальные линии заключены все вычисления, которые
являются подготовительными для применения формулы интегрирования по
частям. Подготовительные записи могут быть вынесены за пределы уравнения.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Задача. Найти приращение функции, первообразной для функции f(x), при
переходе аргумента х от значения а к значению b.
Решение. Положим, что интегрированием найдено
Как видим, в выражении приращения первообразной функции F(x) + С 1
отсутствует постоянная величина С 1 . А так как под С 1 подразумевалось любое
данное число, то полученный результат приводит к следующему заключению: при
переходе аргумента х от значения х=а к значению х=b все функции F(x) + С,
первообразные для данной функции f(x), имеют одно и то же приращение, равное
F(b)-F(a).
Это приращение принято называть определенным интегралом и обозначать
символом
Таким образом, искомый интеграл равен 6.
Геометрический смысл определенного интеграла
1. Найти площадь одной арки синусоиды.
Тело вращения изображено на рисунке.
В качестве плоскости я выберем плоскость ху.
Пример №2. Нахождение определенного интеграла методом замены переменной
интегрирования
Пример №3. Нахождение определенного интеграла методом интегрирования по
частям.
Соотношения между массой m и плотностью р:
Соотношения между электрическим зарядом q и силой тока I:
Соотношения между теплоёмкостью с и количеством теплоты Q:
Описание движения вязкой жидкости, крови по сосудам, распределения
давления крови в сердечнососудистой системе, тепловых, электрических,
магнитных, оптических процессов, связанных с жизнедеятельностью
организма, требует применение интегрирования.
ТРЕНИНГ: РЕШЕНИЕ ПРИМЕРОВ
точки меняется по закону v = (6t +7) м/с
Определить, как зависит от времени пройденный путь, если скорость материальной
точки меняется по закону v = (6t +7)м/с, если известно, что в начальный момент
времени (t=0), материальная точка находилась на расстоянии s 0 = 4м от начала
Найти работу, совершаемую пружиной при её удлинении от x 1 до х 2 .
Решение.
Чтобы проинтегрировать данную функцию, необходимо сделать замену
переменной
Гак как 4-х 2 ≤2-х на отрезке [-1;2], то площадь S данной фигуры вычисляется
следующим образом:
Решение.
u = sinx
du = cosxdx
новые пределы интегрирования: u 1 = 0 (т.к. x 1 = 0, подставим это значение в новую
функцию - u = sinx, u 1 = sinx 1 = 0)
возникновении в нем индукционного тока,
| |
| ответ: |
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференциальные уравнения - это уравнения, содержащие искомые
функции, их производные различных порядков и независимые переменные.
Теория дифференциальных уравнений возникла в конце 17 века под
влиянием потребностей механики и других естественнонаучных дисциплин,
по существу одновременно с интегральным исчислением и
дифференциальным исчислением.
Простейшие дифференциальные уравнения встречались уже в работах И.
Ньютона и Г. Лейбница; термин "дифференциальные уравнения"
принадлежит Лейбницу. Задачу нахождения неопределённого интеграла F (х)
функции f(x) Ньютон рассматривал просто как частный случай его второй
задачи. Такой подход был для Ньютона, как создателя основ
математического естествознания вполне оправданным: в очень большом
числе случаев законы природы, управляющие теми или иными процессами,
выражаются в форме дифференциальных уравнений, а расчёт течения этих
процессов сводится к решению дифференциальных уравнений.
Следующие два простых примера могут служить иллюстрацией к
сказанному.
1) Если тело, нагретое до температуры Т, помещено в среду, температура
которой равна нулю, то при известных условиях можно считать, что
приращение ΔТ(отрицательное в случае Т> 0) его температуры за малый
промежуток времени Δt с достаточной точностью выражается формулой
где k - постоянный коэффициент. При математической обработке этой
физической задачи считают, что выполняется точно соответствующее
предельное соотношение между дифференциалами
т. е. имеет место дифференциальное уравнение
где Т обозначает производную no t.
растяжения пружины, приводят груз в
движение. Если х (t) обозначает
величину отклонения тела от
положения равновесия в момент
времени t, то ускорение тела
выражается 2-й производной х" (t).
Сила тх" (t), действующая на тело,
при небольших растяжениях пружины
по законам теории упругости пропорциональна отклонению х (t). Т. о.,
получается дифференциальное уравнение
 |
| Его решение имеет вид: |