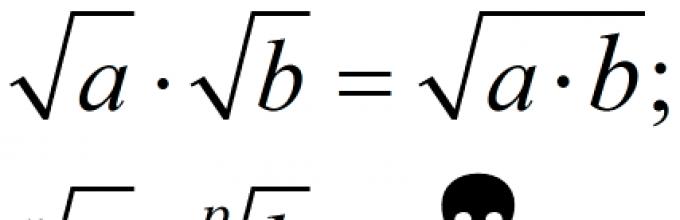Η ν η ρίζα και οι βασικές της ιδιότητες. Χρήση των ιδιοτήτων των ριζών κατά τον μετασχηματισμό παράλογων παραστάσεων, παραδειγμάτων, λύσεων Μετασχηματισμός παραστάσεων με αριθμούς κάτω από τα σημάδια των ριζών

Ξανακοίταξα την πινακίδα... Και, πάμε!

Ας ξεκινήσουμε με κάτι απλό:

Μισό λεπτό. αυτό, που σημαίνει ότι μπορούμε να το γράψουμε ως εξής:

Το έπιασα; Εδώ είναι το επόμενο για εσάς:

Δεν εξάγονται ακριβώς οι ρίζες των αριθμών που προκύπτουν; Κανένα πρόβλημα - εδώ είναι μερικά παραδείγματα:

Τι γίνεται αν δεν υπάρχουν δύο, αλλά περισσότεροι πολλαπλασιαστές; Το ίδιο! Ο τύπος για τον πολλαπλασιασμό των ριζών λειτουργεί με οποιονδήποτε αριθμό παραγόντων:

Τώρα εντελώς μόνοι σας:

Απαντήσεις:Μπράβο! Συμφωνώ, όλα είναι πολύ εύκολα, το κύριο πράγμα είναι να γνωρίζετε τον πίνακα πολλαπλασιασμού!

Διαίρεση ρίζας

Τακτοποιήσαμε τον πολλαπλασιασμό των ριζών, τώρα ας προχωρήσουμε στην ιδιότητα της διαίρεσης.

Να σας υπενθυμίσω ότι η φόρμουλα στο γενική εικόναμοιάζει με αυτό:

Το οποίο σημαίνει ότι η ρίζα του πηλίκου είναι ίση με το πηλίκο των ριζών.

Λοιπόν, ας δούμε μερικά παραδείγματα:

Αυτό είναι όλη η επιστήμη. Εδώ είναι ένα παράδειγμα:

Όλα δεν είναι τόσο ομαλά όσο στο πρώτο παράδειγμα, αλλά, όπως μπορείτε να δείτε, δεν υπάρχει τίποτα περίπλοκο.

Τι γίνεται αν συναντήσετε αυτήν την έκφραση:

Απλά πρέπει να εφαρμόσετε τον τύπο προς την αντίθετη κατεύθυνση:

Και ιδού ένα παράδειγμα:

Μπορεί επίσης να συναντήσετε αυτήν την έκφραση:

Όλα είναι ίδια, μόνο εδώ πρέπει να θυμάστε πώς να μεταφράζετε κλάσματα (αν δεν θυμάστε, κοιτάξτε το θέμα και επιστρέψτε!). Θυμάσαι; Τώρα ας αποφασίσουμε!

Είμαι βέβαιος ότι έχετε αντιμετωπίσει τα πάντα, τώρα ας προσπαθήσουμε να ανεβάσουμε τις ρίζες σε βαθμούς.

Εκθεσιμότητα

Τι συμβαίνει αν η τετραγωνική ρίζα είναι στο τετράγωνο; Είναι απλό, θυμηθείτε την έννοια της τετραγωνικής ρίζας ενός αριθμού - αυτός είναι ένας αριθμός του οποίου η τετραγωνική ρίζα είναι ίση με.

Λοιπόν, αν τετραγωνίσουμε έναν αριθμό του οποίου η τετραγωνική ρίζα είναι ίση, τι παίρνουμε;

Λοιπόν, φυσικά,!

Ας δούμε παραδείγματα:

Είναι απλό, σωστά; Τι γίνεται αν η ρίζα είναι σε διαφορετικό βαθμό; Είναι εντάξει!

Ακολουθήστε την ίδια λογική και θυμηθείτε τις ιδιότητες και τις πιθανές ενέργειες με μοίρες.

Διαβάστε τη θεωρία για το θέμα "" και όλα θα σας γίνουν εξαιρετικά ξεκάθαρα.

Για παράδειγμα, εδώ είναι μια έκφραση:

Σε αυτό το παράδειγμα, ο βαθμός είναι άρτιος, αλλά τι γίνεται αν είναι περιττός; Και πάλι, εφαρμόστε τις ιδιότητες των εκθετών και συνυπολογίστε τα πάντα:

Όλα φαίνονται ξεκάθαρα με αυτό, αλλά πώς να εξαγάγετε τη ρίζα ενός αριθμού σε μια δύναμη; Εδώ, για παράδειγμα, είναι αυτό:

Πολύ απλό, σωστά; Τι γίνεται αν ο βαθμός είναι μεγαλύτερος από δύο; Ακολουθούμε την ίδια λογική χρησιμοποιώντας τις ιδιότητες των μοιρών:

Λοιπόν, είναι όλα ξεκάθαρα; Στη συνέχεια, λύστε μόνοι σας τα παραδείγματα:

Και ιδού οι απαντήσεις:

Μπαίνοντας κάτω από το σημάδι της ρίζας

Τι δεν μάθαμε να κάνουμε με τις ρίζες! Το μόνο που μένει είναι να εξασκηθείτε στην εισαγωγή του αριθμού κάτω από το σύμβολο της ρίζας!

Είναι πραγματικά εύκολο!

Ας πούμε ότι έχουμε έναν αριθμό γραμμένο

Τι μπορούμε να κάνουμε με αυτό; Λοιπόν, φυσικά, κρύψτε τα τρία κάτω από τη ρίζα, να θυμάστε ότι το τρία είναι η τετραγωνική ρίζα του!

Για τι το χρειαζόμαστε αυτό; Ναι, απλώς για να επεκτείνουμε τις δυνατότητές μας κατά την επίλυση παραδειγμάτων:

Πώς σας αρέσει αυτή η ιδιότητα των ριζών; Κάνει τη ζωή πολύ πιο εύκολη; Για μένα, αυτό ακριβώς είναι! Μόνο Πρέπει να θυμόμαστε ότι μπορούμε να εισάγουμε θετικούς αριθμούς μόνο κάτω από το σύμβολο της τετραγωνικής ρίζας.

Λύστε μόνοι σας αυτό το παράδειγμα -
Κατάφερες; Ας δούμε τι πρέπει να πάρετε:

Μπράβο! Καταφέρατε να εισάγετε τον αριθμό κάτω από το σύμβολο της ρίζας! Ας προχωρήσουμε σε κάτι εξίσου σημαντικό - ας δούμε πώς να συγκρίνουμε αριθμούς που περιέχουν τετραγωνική ρίζα!

Σύγκριση ριζών

Γιατί πρέπει να μάθουμε να συγκρίνουμε αριθμούς που περιέχουν τετραγωνική ρίζα;

Πολύ απλό. Συχνά, σε μεγάλες και μεγάλες εκφράσεις που συναντάμε στις εξετάσεις, λαμβάνουμε μια παράλογη απάντηση (θυμηθείτε τι είναι αυτό; Το έχουμε ήδη μιλήσει σήμερα!)

Πρέπει να τοποθετήσουμε τις λαμβανόμενες απαντήσεις στη γραμμή συντεταγμένων, για παράδειγμα, για να καθορίσουμε ποιο διάστημα είναι κατάλληλο για την επίλυση της εξίσωσης. Και εδώ προκύπτει το πρόβλημα: δεν υπάρχει αριθμομηχανή στις εξετάσεις, και χωρίς αυτήν, πώς μπορείτε να φανταστείτε ποιος αριθμός είναι μεγαλύτερος και ποιος μικρότερος; Αυτό είναι!

Για παράδειγμα, προσδιορίστε ποιο είναι μεγαλύτερο: ή;

Δεν μπορείς να πεις αμέσως. Λοιπόν, ας χρησιμοποιήσουμε την αποσυναρμολογημένη ιδιότητα της εισαγωγής ενός αριθμού κάτω από το σύμβολο της ρίζας;

Τότε προχωρήστε:

Λοιπόν, προφανώς, τι μεγαλύτερο αριθμόκάτω από το σημάδι της ρίζας, τόσο μεγαλύτερη είναι η ίδια η ρίζα!

Εκείνοι. αν τότε, .

Από αυτό συμπεραίνουμε σταθερά ότι. Και κανείς δεν θα μας πείσει για το αντίθετο!

Εξαγωγή ριζών από μεγάλους αριθμούς

Πριν από αυτό, εισάγαμε έναν πολλαπλασιαστή κάτω από το σύμβολο της ρίζας, αλλά πώς να τον αφαιρέσουμε; Απλά πρέπει να το συνυπολογίσετε σε παράγοντες και να εξαγάγετε ό,τι εξάγετε!

Ήταν δυνατό να ακολουθήσουμε έναν διαφορετικό δρόμο και να επεκταθούμε σε άλλους παράγοντες:

Δεν είναι κακό, σωστά; Οποιαδήποτε από αυτές τις προσεγγίσεις είναι σωστή, αποφασίστε όπως θέλετε.

Το Factoring είναι πολύ χρήσιμο κατά την επίλυση τέτοιων μη τυπικών προβλημάτων όπως αυτό:

Ας μην φοβόμαστε, αλλά πράξτε! Ας αποσυνθέσουμε κάθε παράγοντα κάτω από τη ρίζα σε ξεχωριστούς παράγοντες:

Τώρα δοκιμάστε το μόνοι σας (χωρίς αριθμομηχανή! Δεν θα είναι στις εξετάσεις):

Είναι αυτό το τέλος; Ας μην σταματήσουμε στα μισά!

Αυτό είναι όλο, δεν είναι τόσο τρομακτικό, σωστά;

Συνέβη; Μπράβο, έτσι είναι!

Τώρα δοκιμάστε αυτό το παράδειγμα:

Αλλά το παράδειγμα είναι ένα σκληρό καρύδι, οπότε δεν μπορείτε να καταλάβετε αμέσως πώς να το προσεγγίσετε. Αλλά, φυσικά, μπορούμε να το διαχειριστούμε.

Λοιπόν, ας ξεκινήσουμε το factoring; Ας σημειώσουμε αμέσως ότι μπορείτε να διαιρέσετε έναν αριθμό με (θυμηθείτε τα σημάδια της διαιρετότητας):

Τώρα, δοκιμάστε το μόνοι σας (και πάλι, χωρίς αριθμομηχανή!):

Λοιπόν, λειτούργησε; Μπράβο, έτσι είναι!

Ας το συνοψίσουμε

1. Η τετραγωνική ρίζα (αριθμητική τετραγωνική ρίζα) του μη αρνητικός αριθμόςΚαλείται ένας μη αρνητικός αριθμός του οποίου το τετράγωνο είναι ίσο με.
   .
2. Εάν πάρουμε απλώς την τετραγωνική ρίζα ενός πράγματος, παίρνουμε πάντα ένα μη αρνητικό αποτέλεσμα.
3. Ιδιότητες αριθμητικής ρίζας:
4. Κατά τη σύγκριση τετραγωνικές ρίζεςείναι απαραίτητο να θυμάστε ότι όσο μεγαλύτερος είναι ο αριθμός κάτω από το σύμβολο της ρίζας, τόσο μεγαλύτερη είναι η ίδια η ρίζα.

Πώς είναι η τετραγωνική ρίζα; Ολα ΕΝΤΑΞΕΙ;

Προσπαθήσαμε να σας εξηγήσουμε χωρίς φασαρία όλα όσα πρέπει να ξέρετε στις εξετάσεις για την τετραγωνική ρίζα.

Είναι η σειρά σου. Γράψτε μας αν αυτό το θέμα σας είναι δύσκολο ή όχι.

Μάθατε κάτι νέο ή όλα ήταν ήδη ξεκάθαρα;

Γράψτε στα σχόλια και καλή επιτυχία στις εξετάσεις σας!

Χαιρετίσματα, γάτες! Την τελευταία φορά συζητήσαμε λεπτομερώς τι είναι οι ρίζες (αν δεν θυμάστε, προτείνω να το διαβάσετε). Το κύριο στοιχείο από αυτό το μάθημα: υπάρχει μόνο ένας καθολικός ορισμός των ριζών, που είναι αυτό που πρέπει να γνωρίζετε. Τα υπόλοιπα είναι ανοησίες και χάσιμο χρόνου.

Σήμερα πάμε παρακάτω. Θα μάθουμε να πολλαπλασιάζουμε ρίζες, θα μελετήσουμε κάποια προβλήματα που σχετίζονται με τον πολλαπλασιασμό (αν δεν λυθούν αυτά τα προβλήματα μπορεί να γίνουν μοιραία στις εξετάσεις) και θα εξασκηθούμε σωστά. Προμηθευτείτε λοιπόν ποπ κορν, νιώστε άνετα και ας ξεκινήσουμε.

Ούτε εσύ δεν το έχεις καπνίσει ακόμα, έτσι δεν είναι;

Το μάθημα αποδείχθηκε αρκετά μεγάλο, οπότε το χώρισα σε δύο μέρη:

1. Αρχικά θα δούμε τους κανόνες του πολλαπλασιασμού. Το Cap φαίνεται να υπαινίσσεται: αυτό συμβαίνει όταν υπάρχουν δύο ρίζες, μεταξύ τους υπάρχει ένα σημάδι "πολλαπλασιασμού" - και θέλουμε να κάνουμε κάτι με αυτό.
2. Στη συνέχεια, ας δούμε την αντίθετη κατάσταση: υπάρχει μια μεγάλη ρίζα, αλλά ήμασταν πρόθυμοι να την αναπαραστήσουμε ως προϊόν δύο απλούστερων ριζών. Γιατί είναι απαραίτητο αυτό, είναι ένα ξεχωριστό ερώτημα. Θα αναλύσουμε μόνο τον αλγόριθμο.

Για όσους ανυπομονούν να περάσουν αμέσως στο δεύτερο μέρος, είστε ευπρόσδεκτοι. Ας ξεκινήσουμε με τα υπόλοιπα με τη σειρά.

Βασικός κανόνας πολλαπλασιασμού

Ας ξεκινήσουμε με το πιο απλό πράγμα - τις κλασικές τετραγωνικές ρίζες. Τα ίδια που συμβολίζονται με $\sqrt(a)$ και $\sqrt(b)$. Όλα είναι προφανή για αυτούς:

Κανόνας πολλαπλασιασμού. Για να πολλαπλασιάσετε μια τετραγωνική ρίζα με μια άλλη, απλώς πολλαπλασιάζετε τις ριζικές εκφράσεις τους και γράφετε το αποτέλεσμα κάτω από την κοινή ρίζα:

\[\sqrt(a)\cdot \sqrt(b)=\sqrt(a\cdot b)\]

Δεν επιβάλλονται πρόσθετοι περιορισμοί στους αριθμούς στα δεξιά ή στα αριστερά: εάν υπάρχουν οι ριζικοί παράγοντες, τότε υπάρχει και το προϊόν.

Παραδείγματα. Ας δούμε τέσσερα παραδείγματα με αριθμούς ταυτόχρονα:

\[\begin(align) & \sqrt(25)\cdot \sqrt(4)=\sqrt(25\cdot 4)=\sqrt(100)=10; \\ & \sqrt(32)\cdot \sqrt(2)=\sqrt(32\cdot 2)=\sqrt(64)=8; \\ & \sqrt(54)\cdot \sqrt(6)=\sqrt(54\cdot 6)=\sqrt(324)=18; \\ & \sqrt(\frac(3)(17))\cdot \sqrt(\frac(17)(27))=\sqrt(\frac(3)(17)\cdot \frac(17)(27 ))=\sqrt(\frac(1)(9))=\frac(1)(3). \\ \end(στοίχιση)\]

Όπως μπορείτε να δείτε, το κύριο σημείο αυτού του κανόνα είναι η απλοποίηση παράλογες εκφράσεις. Και αν στο πρώτο παράδειγμα εμείς οι ίδιοι θα είχαμε εξαγάγει τις ρίζες του 25 και του 4 χωρίς νέους κανόνες, τότε τα πράγματα γίνονται δύσκολα: τα $\sqrt(32)$ και τα $\sqrt(2)$ δεν θεωρούνται από μόνα τους, αλλά Το γινόμενο τους αποδεικνύεται τέλειο τετράγωνο, επομένως η ρίζα του είναι ίση με έναν ρητό αριθμό.

Θα ήθελα ιδιαίτερα να επισημάνω την τελευταία γραμμή. Εκεί, και οι δύο ριζικές εκφράσεις είναι κλάσματα. Χάρη στο προϊόν, πολλοί παράγοντες ακυρώνονται και ολόκληρη η έκφραση μετατρέπεται σε επαρκή αριθμό.

Φυσικά, τα πράγματα δεν θα είναι πάντα τόσο όμορφα. Μερικές φορές θα υπάρχει ένα πλήρες χάος κάτω από τις ρίζες - δεν είναι σαφές τι να το κάνετε και πώς να το μεταμορφώσετε μετά τον πολλαπλασιασμό. Λίγο αργότερα, όταν αρχίσετε να μελετάτε τις παράλογες εξισώσεις και ανισότητες, θα υπάρχουν κάθε λογής μεταβλητές και συναρτήσεις. Και πολύ συχνά, οι συγγραφείς προβλημάτων βασίζονται στο γεγονός ότι θα ανακαλύψετε ορισμένους όρους ή παράγοντες ακύρωσης, μετά τους οποίους το πρόβλημα θα απλοποιηθεί πολλές φορές.

Επιπλέον, δεν είναι καθόλου απαραίτητο να πολλαπλασιαστούν ακριβώς δύο ρίζες. Μπορείτε να πολλαπλασιάσετε τρία, τέσσερα ή και δέκα ταυτόχρονα! Αυτό δεν θα αλλάξει τον κανόνα. Ρίξε μια ματιά:

\[\begin(align) & \sqrt(2)\cdot \sqrt(3)\cdot \sqrt(6)=\sqrt(2\cdot 3\cdot 6)=\sqrt(36)=6; \\ & \sqrt(5)\cdot \sqrt(2)\cdot \sqrt(0.001)=\sqrt(5\cdot 2\cdot 0.001)= \\ & =\sqrt(10\cdot \frac(1) (1000))=\sqrt(\frac(1)(100))=\frac(1)(10). \\ \end(στοίχιση)\]

Και πάλι μια μικρή σημείωση για το δεύτερο παράδειγμα. Όπως μπορείτε να δείτε, στον τρίτο παράγοντα κάτω από τη ρίζα υπάρχει ένα δεκαδικό κλάσμα - στη διαδικασία των υπολογισμών το αντικαθιστούμε με ένα κανονικό, μετά το οποίο όλα μειώνονται εύκολα. Έτσι: Συνιστώ ανεπιφύλακτα να απαλλαγείτε από δεκαδικά κλάσματα σε οποιεσδήποτε παράλογες εκφράσεις (δηλαδή που περιέχουν τουλάχιστον ένα ριζικό σύμβολο). Αυτό θα σας εξοικονομήσει πολύ χρόνο και νεύρα στο μέλλον.

Αλλά αυτό ήταν μια λυρική παρέκβαση. Ας εξετάσουμε τώρα μια πιο γενική περίπτωση - όταν ο ριζικός εκθέτης περιέχει έναν αυθαίρετο αριθμό $n$, και όχι μόνο τον "κλασικό" δύο.

Η περίπτωση ενός αυθαίρετου δείκτη

Λοιπόν, τακτοποιήσαμε τις τετραγωνικές ρίζες. Τι να κάνουμε με τα κυβικά; Ή ακόμα και με ρίζες αυθαίρετου βαθμού $n$; Ναι, όλα είναι ίδια. Ο κανόνας παραμένει ο ίδιος:

Για να πολλαπλασιάσουμε δύο ρίζες βαθμού $n$, αρκεί να πολλαπλασιάσουμε τις ριζικές εκφράσεις τους και μετά να γράψουμε το αποτέλεσμα κάτω από μία ρίζα.

Γενικά, τίποτα περίπλοκο. Εκτός από το ότι το ποσό των υπολογισμών μπορεί να είναι μεγαλύτερο. Ας δούμε μερικά παραδείγματα:

Παραδείγματα. Υπολογισμός προϊόντων:

\[\begin(align) & \sqrt(20)\cdot \sqrt(\frac(125)(4))=\sqrt(20\cdot \frac(125)(4))=\sqrt(625)= 5; \\ & \sqrt(\frac(16)(625))\cdot \sqrt(0,16)=\sqrt(\frac(16)(625)\cdot \frac(16)(100))=\sqrt (\ frac(64)(((25)^(2))\cdot 25))= \\ & =\sqrt(\frac(((4)^(3)))(((25)^(3 )) ))=\sqrt(((\left(\frac(4)(25) \right))^(3)))=\frac(4)(25). \\ \end(στοίχιση)\]

Και πάλι προσοχή στη δεύτερη έκφραση. Πολλαπλασιάζουμε κυβικές ρίζες, απαλλαγούμε δεκαδικόςκαι ως αποτέλεσμα παίρνουμε το γινόμενο των αριθμών 625 και 25 στον παρονομαστή μεγάλος αριθμός- Προσωπικά, δεν μπορώ να υπολογίσω αμέσως με τι ισούται.

Επομένως, απλώς απομονώσαμε τον ακριβή κύβο στον αριθμητή και στον παρονομαστή και, στη συνέχεια, χρησιμοποιήσαμε μία από τις βασικές ιδιότητες (ή, αν προτιμάτε, ορισμό) της ρίζας $n$th:

\[\begin(align) & \sqrt(((a)^(2n+1)))=a; \\ & \sqrt(((a)^(2n)))=\αριστερά| a\σωστά|. \\ \end(στοίχιση)\]

Τέτοιες «μηχανουργίες» μπορούν να σας εξοικονομήσουν πολύ χρόνο στις εξετάσεις ή δοκιμαστική εργασία, θυμηθείτε λοιπόν:

Μην βιαστείτε να πολλαπλασιάσετε αριθμούς χρησιμοποιώντας ριζικές εκφράσεις. Πρώτα, ελέγξτε: τι γίνεται αν ο ακριβής βαθμός οποιασδήποτε έκφρασης είναι "κρυπτογραφημένος" εκεί;

Παρά το προφανές αυτής της παρατήρησης, οφείλω να ομολογήσω ότι οι περισσότεροι απροετοίμαστοι μαθητές δεν βλέπουν τους ακριβείς βαθμούς σε εύρος κενού σημείου. Αντίθετα, πολλαπλασιάζουν τα πάντα και μετά αναρωτιούνται: γιατί πήραν τόσο βάναυσους αριθμούς;

Ωστόσο, όλα αυτά είναι κουβέντα μωρού σε σύγκριση με αυτά που θα μελετήσουμε τώρα.

Πολλαπλασιασμός ριζών με διαφορετικούς εκθέτες

Εντάξει, τώρα μπορούμε να πολλαπλασιάσουμε τις ρίζες με τους ίδιους δείκτες. Τι γίνεται αν οι δείκτες είναι διαφορετικοί; Ας πούμε, πώς να πολλαπλασιάσετε ένα συνηθισμένο $\sqrt(2)$ με κάποια χάλια όπως $\sqrt(23)$; Είναι καν δυνατό να γίνει αυτό;

Ναι φυσικά μπορείς. Όλα γίνονται σύμφωνα με αυτόν τον τύπο:

Κανόνας για τον πολλαπλασιασμό των ριζών. Για να πολλαπλασιάσετε το $\sqrt[n](a)$ με το $\sqrt[p](b)$, αρκεί να εκτελέσετε τον ακόλουθο μετασχηματισμό:

\[\sqrt[n](a)\cdot \sqrt[p](b)=\sqrt(((a)^(p))\cdot ((b)^(n)))\]

Ωστόσο, αυτός ο τύπος λειτουργεί μόνο εάν Οι ριζικές εκφράσεις είναι μη αρνητικές. Αυτή είναι μια πολύ σημαντική σημείωση στην οποία θα επανέλθουμε λίγο αργότερα.

Προς το παρόν, ας δούμε μερικά παραδείγματα:

\[\begin(align) & \sqrt(3)\cdot \sqrt(2)=\sqrt(((3)^(4))\cdot ((2)^(3)))=\sqrt(81 \cdot 8)=\sqrt(648); \\ & \sqrt(2)\cdot \sqrt(7)=\sqrt(((2)^(5))\cdot ((7)^(2))=\sqrt(32\cdot 49)= \sqrt(1568); \\ & \sqrt(5)\cdot \sqrt(3)=\sqrt(((5)^(4))\cdot ((3)^(2))=\sqrt(625\cdot 9)= \sqrt(5625). \\ \end(στοίχιση)\]

Όπως μπορείτε να δείτε, τίποτα περίπλοκο. Τώρα ας καταλάβουμε από πού προήλθε η απαίτηση μη αρνητικότητας και τι θα συμβεί αν την παραβιάσουμε.

Ο πολλαπλασιασμός των ριζών είναι εύκολος

Γιατί οι ριζοσπαστικές εκφράσεις πρέπει να είναι μη αρνητικές;

Φυσικά μπορείς να είσαι σαν δασκάλους του σχολείουκαι παραθέτω έξυπνα το σχολικό βιβλίο:

Η απαίτηση μη αρνητικότητας σχετίζεται με διαφορετικούς ορισμούςρίζες ζυγών και περιττών βαθμών (ανάλογα, οι τομείς ορισμού τους είναι επίσης διαφορετικοί).

Λοιπόν, έγινε πιο ξεκάθαρο; Προσωπικά, όταν διάβασα αυτή τη βλακεία στην 8η δημοτικού, κατάλαβα κάτι σαν το εξής: «Η απαίτηση της μη αρνητικότητας συνδέεται με το *#&^@(*#@^#)~%» - εν ολίγοις, το έκανα Δεν καταλαβαίνω τίποτα εκείνη τη στιγμή.

Τώρα λοιπόν θα εξηγήσω τα πάντα με κανονικό τρόπο.

Αρχικά, ας μάθουμε από πού προέρχεται ο παραπάνω τύπος πολλαπλασιασμού. Για να το κάνετε αυτό, επιτρέψτε μου να σας υπενθυμίσω μια σημαντική ιδιότητα της ρίζας:

\[\sqrt[n](a)=\sqrt(((a)^(k)))\]

Με άλλα λόγια, μπορούμε εύκολα να αυξήσουμε τη ριζική έκφραση σε οποιαδήποτε φυσική δύναμη $k$ - σε αυτήν την περίπτωση, ο εκθέτης της ρίζας θα πρέπει να πολλαπλασιαστεί με την ίδια ισχύ. Επομένως, μπορούμε εύκολα να μειώσουμε οποιεσδήποτε ρίζες σε έναν κοινό εκθέτη και μετά να τις πολλαπλασιάσουμε. Από εδώ προέρχεται ο τύπος πολλαπλασιασμού:

\[\sqrt[n](a)\cdot \sqrt[p](b)=\sqrt(((a)^(p)))\cdot \sqrt(((b)^(n)))= \sqrt(((a)^(p))\cdot ((b)^(n)))\]

Αλλά υπάρχει ένα πρόβλημα που περιορίζει δραστικά τη χρήση όλων αυτών των τύπων. Σκεφτείτε αυτόν τον αριθμό:

Σύμφωνα με τον τύπο που μόλις δόθηκε, μπορούμε να προσθέσουμε οποιοδήποτε βαθμό. Ας προσπαθήσουμε να προσθέσουμε $k=2$:

\[\sqrt(-5)=\sqrt(((\left(-5 \right))^(2)))=\sqrt(((5)^(2)))\]

Αφαιρέσαμε το μείον ακριβώς γιατί το τετράγωνο καίει το μείον (όπως κάθε άλλο ζυγό βαθμό). Τώρα ας το κάνουμε αντίστροφη μετατροπή: «μειώστε» δύο σε εκθέτη και δύναμη. Μετά από όλα, οποιαδήποτε ισότητα μπορεί να διαβαστεί τόσο από αριστερά προς τα δεξιά όσο και από τα δεξιά προς τα αριστερά:

\[\begin(align) & \sqrt[n](a)=\sqrt(((a)^(k)))\Rightarrow \sqrt(((a)^(k)))=\sqrt[n ](ένα); \\ & \sqrt(((a)^(k)))=\sqrt[n](a)\Rightarrow \sqrt((((5)^(2)))=\sqrt(((5)^( 2)))=\sqrt(5). \\ \end(στοίχιση)\]

Αλλά μετά αποδεικνύεται ότι είναι κάποιο είδος χάλια:

\[\sqrt(-5)=\sqrt(5)\]

Αυτό δεν μπορεί να συμβεί, γιατί $\sqrt(-5) \lt 0$ και $\sqrt(5) \gt 0$. Αυτό σημαίνει ότι για ζυγές δυνάμεις και αρνητικούς αριθμούς ο τύπος μας δεν λειτουργεί πλέον. Μετά από αυτό έχουμε δύο επιλογές:

1. Να χτυπήσει τον τοίχο και να δηλώσει ότι τα μαθηματικά είναι μια ηλίθια επιστήμη, όπου «υπάρχουν κάποιοι κανόνες, αλλά αυτοί είναι ανακριβείς».
2. Εισαγάγετε πρόσθετους περιορισμούς βάσει των οποίων η φόρμουλα θα λειτουργεί 100%.

Στην πρώτη επιλογή, θα πρέπει να πιάνουμε συνεχώς περιπτώσεις "μη λειτουργικές" - είναι δύσκολο, χρονοβόρο και γενικά ουφ. Ως εκ τούτου, οι μαθηματικοί προτίμησαν τη δεύτερη επιλογή.

Αλλά μην ανησυχείτε! Στην πράξη, αυτός ο περιορισμός δεν επηρεάζει με κανέναν τρόπο τους υπολογισμούς, επειδή όλα τα προβλήματα που περιγράφονται αφορούν μόνο ρίζες περιττού βαθμού και μπορούν να ληφθούν τα μείον από αυτά.

Επομένως, ας διατυπώσουμε έναν ακόμη κανόνα, ο οποίος ισχύει γενικά για όλες τις ενέργειες με ρίζες:

Πριν πολλαπλασιάσετε τις ρίζες, βεβαιωθείτε ότι οι ριζικές εκφράσεις είναι μη αρνητικές.

Παράδειγμα. Στον αριθμό $\sqrt(-5)$ μπορείτε να αφαιρέσετε το μείον κάτω από το σύμβολο της ρίζας - τότε όλα θα είναι κανονικά:

\[\begin(align) & \sqrt(-5)=-\sqrt(5) \lt 0\Right arrow \\ & \sqrt(-5)=-\sqrt(((5)^(2))) =-\sqrt(25)=-\sqrt(((5)^(2)))=-\sqrt(5) \lt 0 \\ \end(στοίχιση)\]

Νιώθεις τη διαφορά; Εάν αφήσετε ένα μείον κάτω από τη ρίζα, τότε όταν η ριζική έκφραση τετραγωνιστεί, θα εξαφανιστεί και θα αρχίσουν τα χάλια. Και αν πρώτα αφαιρέσετε το μείον, τότε μπορείτε να τετραγωνίσετε/αφαιρέσετε μέχρι να γίνετε μπλε στο πρόσωπο - ο αριθμός θα παραμείνει αρνητικός.

Έτσι, ο πιο σωστός και πιο αξιόπιστος τρόπος πολλαπλασιασμού των ριζών είναι ο εξής:

1. Αφαιρέστε όλα τα αρνητικά από τις ρίζες. Τα μειονεκτήματα υπάρχουν μόνο σε ρίζες περιττής πολλαπλότητας - μπορούν να τοποθετηθούν μπροστά από τη ρίζα και, εάν είναι απαραίτητο, να μειωθούν (για παράδειγμα, εάν υπάρχουν δύο από αυτά τα μείον).
2. Εκτελέστε τον πολλαπλασιασμό σύμφωνα με τους κανόνες που συζητήθηκαν παραπάνω στο σημερινό μάθημα. Αν οι δείκτες των ριζών είναι ίδιοι, απλώς πολλαπλασιάζουμε τις ριζικές εκφράσεις. Και αν είναι διαφορετικά, χρησιμοποιούμε τον κακό τύπο \[\sqrt[n](a)\cdot \sqrt[p](b)=\sqrt(((a)^(p))\cdot ((b) ^(n) ))\].
3. 3.Απολαύστε το αποτέλεσμα και καλούς βαθμούς.:)

Καλά; Να ασκηθούμε;

Παράδειγμα 1: Απλοποιήστε την έκφραση:

\[\begin(align) & \sqrt(48)\cdot \sqrt(-\frac(4)(3))=\sqrt(48)\cdot \left(-\sqrt(\frac(4)(3 ) )) \right)=-\sqrt(48)\cdot \sqrt(\frac(4)(3))= \\ & =-\sqrt(48\cdot \frac(4)(3))=- \ sqrt(64)=-4; \end(στοίχιση)\]

Αυτή είναι η απλούστερη επιλογή: οι ρίζες είναι ίδιες και περίεργες, το μόνο πρόβλημα είναι ότι ο δεύτερος παράγοντας είναι αρνητικός. Αφαιρούμε αυτό το μείον από την εικόνα, μετά το οποίο υπολογίζονται εύκολα όλα.

Παράδειγμα 2: Απλοποιήστε την έκφραση:

\[\begin(align) & \sqrt(32)\cdot \sqrt(4)=\sqrt(((2)^(5)))\cdot \sqrt(((2)^(2))= \sqrt(((\left(((2)^(5)) \right))^(3))\cdot ((\left(((2)^(2)) \δεξιά))^(4) ))= \\ & =\sqrt(((2)^(15))\cdot ((2)^(8)))=\sqrt(((2)^(23))) \\ \end( ευθυγραμμίζω)\]

Πολλοί εδώ θα μπερδεύονταν με αυτό που συνέβη στο τέλος παράλογος αριθμός. Ναι, συμβαίνει: δεν μπορέσαμε να απαλλαγούμε εντελώς από τη ρίζα, αλλά τουλάχιστον απλοποιήσαμε σημαντικά την έκφραση.

Παράδειγμα 3: Απλοποιήστε την έκφραση:

\[\begin(align) & \sqrt(a)\cdot \sqrt(((a)^(4)))=\sqrt(((a)^(3))\cdot ((\left((( a)^(4)) \δεξιά))^(6))=\sqrt(((a)^(3))\cdot ((a)^(24)))= \\ & =\sqrt( ((a)^(27)))=\sqrt(((a)^(3\cdot 9)))=\sqrt(((a)^(3))) \end(στοίχιση)\]

Θα ήθελα να επιστήσω την προσοχή σας σε αυτό το έργο. Υπάρχουν δύο σημεία εδώ:

1. Η ρίζα δεν είναι ένας συγκεκριμένος αριθμός ή δύναμη, αλλά η μεταβλητή $a$. Με την πρώτη ματιά, αυτό είναι λίγο ασυνήθιστο, αλλά στην πραγματικότητα, κατά την επίλυση μαθηματικά προβλήματαΤις περισσότερες φορές θα πρέπει να αντιμετωπίσετε μεταβλητές.
2. Τελικά καταφέραμε να «μειώσουμε» τον ριζικό δείκτη και το βαθμό στη ριζοσπαστική έκφραση. Αυτό συμβαίνει αρκετά συχνά. Και αυτό σημαίνει ότι ήταν δυνατό να απλοποιηθούν σημαντικά οι υπολογισμοί εάν δεν χρησιμοποιούσατε τον βασικό τύπο.

Για παράδειγμα, θα μπορούσατε να κάνετε αυτό:

\[\begin(align) & \sqrt(a)\cdot \sqrt(((a)^(4)))=\sqrt(a)\cdot \sqrt(((\left((a)^( 4)) \δεξιά))^(2)))=\sqrt(a)\cdot \sqrt(((a)^(8))) \\ & =\sqrt(a\cdot ((a)^( 8)))=\sqrt(((a)^(9)))=\sqrt(((a)^(3\cdot 3)))=\sqrt(((a)^(3))) \ \\end(στοίχιση)\]

Στην πραγματικότητα, όλοι οι μετασχηματισμοί έγιναν μόνο με τη δεύτερη ρίζα. Και αν δεν περιγράψετε λεπτομερώς όλα τα ενδιάμεσα βήματα, τότε στο τέλος το ποσό των υπολογισμών θα μειωθεί σημαντικά.

Στην πραγματικότητα, έχουμε ήδη αντιμετωπίσει μια παρόμοια εργασία παραπάνω όταν λύσαμε το παράδειγμα $\sqrt(5)\cdot \sqrt(3)$. Τώρα μπορεί να γραφτεί πολύ πιο απλά:

\[\begin(align) & \sqrt(5)\cdot \sqrt(3)=\sqrt(((5)^(4))\cdot ((3)^(2)))=\sqrt(( (\left(((5)^(2))\cdot 3 \right))^(2)))= \\ & =\sqrt(((\left(75 \right))^(2))) =\sqrt(75). \end(στοίχιση)\]

Λοιπόν, έχουμε τακτοποιήσει τον πολλαπλασιασμό των ριζών. Τώρα ας εξετάσουμε την αντίστροφη λειτουργία: τι να κάνετε όταν υπάρχει ένα προϊόν κάτω από τη ρίζα;

Το υλικό σε αυτό το άρθρο θα πρέπει να θεωρηθεί ως μέρος του μετασχηματισμού θέματος των παράλογων εκφράσεων. Εδώ θα χρησιμοποιήσουμε παραδείγματα για να αναλύσουμε όλες τις λεπτές αποχρώσεις και τις αποχρώσεις (από τις οποίες υπάρχουν πολλές) που προκύπτουν κατά την εκτέλεση μετασχηματισμών με βάση τις ιδιότητες των ριζών.

Πλοήγηση στη σελίδα.

Ας θυμηθούμε τις ιδιότητες των ριζών

Δεδομένου ότι πρόκειται να ασχοληθούμε με τον μετασχηματισμό των εκφράσεων χρησιμοποιώντας τις ιδιότητες των ριζών, δεν θα σας βλάψει να θυμάστε τις κύριες ή ακόμα καλύτερα, να τις γράψετε σε χαρτί και να τις τοποθετήσετε μπροστά σας.

Πρώτα μελετήθηκε τετραγωνικές ρίζεςκαι τις ακόλουθες ιδιότητες τους (a, b, a 1, a 2, ..., a k είναι πραγματικοί αριθμοί):

Και αργότερα επεκτείνεται η ιδέα της ρίζας, εισάγεται ο ορισμός της ρίζας του nου βαθμού και εξετάζονται οι ακόλουθες ιδιότητες (a, b, a 1, a 2, ..., a k είναι πραγματικοί αριθμοί, m, n, n 1, n 2, ... , n k - φυσικοί αριθμοί):

Μετατροπή εκφράσεων με αριθμούς κάτω από ριζικά πρόσημα

Ως συνήθως, πρώτα μαθαίνουν να εργάζονται με αριθμητικές εκφράσεις και μόνο μετά περνούν σε εκφράσεις με μεταβλητές. Θα κάνουμε το ίδιο, και πρώτα θα ασχοληθούμε με τον μετασχηματισμό των παράλογων εκφράσεων που περιέχουν μόνο αριθμητικές εκφράσεις, και στη συνέχεια στην επόμενη παράγραφο θα εισαγάγουμε μεταβλητές κάτω από τα πρόσημα των ριζών.

Πώς μπορεί να χρησιμοποιηθεί για να μετασχηματίσει εκφράσεις; Είναι πολύ απλό: για παράδειγμα, μπορούμε να αντικαταστήσουμε μια παράλογη έκφραση με μια έκφραση ή το αντίστροφο. Δηλαδή, εάν η έκφραση που μετατρέπεται περιέχει μια έκφραση που ταιριάζει εμφανισιακά με την έκφραση από το αριστερό (δεξιό) μέρος οποιασδήποτε από τις αναφερόμενες ιδιότητες των ριζών, τότε μπορεί να αντικατασταθεί από την αντίστοιχη έκφραση από το δεξιό (αριστερό) μέρος. Αυτός είναι ο μετασχηματισμός των εκφράσεων χρησιμοποιώντας τις ιδιότητες των ριζών.

Ας δώσουμε μερικά ακόμη παραδείγματα.

Ας απλοποιήσουμε την έκφραση . Οι αριθμοί 3, 5 και 7 είναι θετικοί, οπότε μπορούμε να εφαρμόσουμε με ασφάλεια τις ιδιότητες των ριζών. Εδώ μπορείτε να ενεργήσετε με διαφορετικούς τρόπους. Για παράδειγμα, μια ρίζα που βασίζεται σε μια ιδιότητα μπορεί να αναπαρασταθεί ως , και μια ρίζα που χρησιμοποιεί μια ιδιότητα με k=3 - ως , με αυτήν την προσέγγιση η λύση θα μοιάζει με αυτό:

Κάποιος θα μπορούσε να το κάνει διαφορετικά αντικαθιστώντας με , και μετά με , οπότε η λύση θα μοιάζει με αυτό:

Άλλες λύσεις είναι δυνατές, για παράδειγμα:

Ας δούμε τη λύση σε ένα άλλο παράδειγμα. Ας μεταμορφώσουμε την έκφραση. Εξετάζοντας τη λίστα των ιδιοτήτων των ριζών, επιλέγουμε από αυτήν τις ιδιότητες που χρειαζόμαστε για να λύσουμε το παράδειγμα είναι σαφές ότι δύο από αυτές είναι χρήσιμες εδώ και , οι οποίες ισχύουν για οποιοδήποτε α. Εχουμε:

Εναλλακτικά, θα μπορούσε κανείς πρώτα να μετασχηματίσει τις ριζικές εκφράσεις χρησιμοποιώντας

και μετά εφαρμόστε τις ιδιότητες των ριζών

Μέχρι αυτό το σημείο, έχουμε μετατρέψει εκφράσεις που περιέχουν μόνο τετραγωνικές ρίζες. Ήρθε η ώρα να δουλέψετε με ρίζες που έχουν διαφορετικούς δείκτες.

Παράδειγμα.

Μετατρέψτε την παράλογη έκφραση .

Λύση.

Κατά ιδιοκτησία ο πρώτος παράγοντας ενός δεδομένου προϊόντος μπορεί να αντικατασταθεί από τον αριθμό −2:

Προχώρα. Δυνάμει της ιδιότητας, ο δεύτερος παράγοντας μπορεί να αναπαρασταθεί ως , και δεν θα ήταν κακό να αντικατασταθεί το 81 με τετραπλάσια ισχύ τριών, αφού στους υπόλοιπους παράγοντες ο αριθμός 3 εμφανίζεται κάτω από τα σημάδια των ριζών:

Συνιστάται να αντικαταστήσετε τη ρίζα ενός κλάσματος με μια αναλογία ριζών της μορφής, η οποία μπορεί να μετατραπεί περαιτέρω: . Εχουμε

Μετά την εκτέλεση πράξεων με δύο, η έκφραση που προκύπτει θα πάρει τη μορφή , και το μόνο που μένει είναι να μετασχηματίσουμε το γινόμενο των ριζών.

Για τη μετατροπή των προϊόντων των ριζών, συνήθως μειώνονται σε έναν δείκτη, για τον οποίο συνιστάται να λαμβάνονται οι δείκτες όλων των ριζών. Στην περίπτωσή μας, LCM(12, 6, 12) = 12, και μόνο η ρίζα θα πρέπει να μειωθεί σε αυτόν τον δείκτη, αφού οι άλλες δύο ρίζες έχουν ήδη έναν τέτοιο δείκτη. Η ισότητα, η οποία εφαρμόζεται από τα δεξιά προς τα αριστερά, μας επιτρέπει να αντεπεξέλθουμε σε αυτό το έργο. Ετσι . Λαμβάνοντας υπόψη αυτό το αποτέλεσμα, έχουμε

Τώρα το προϊόν των ριζών μπορεί να αντικατασταθεί από τη ρίζα του προϊόντος και να εκτελέσει τους υπόλοιπους, ήδη προφανείς, μετασχηματισμούς:

θα εκδώσουμε σύντομη εκδοχήλύσεις:

Απάντηση:

.

Τονίζουμε ξεχωριστά ότι για την εφαρμογή των ιδιοτήτων των ριζών είναι απαραίτητο να ληφθούν υπόψη οι περιορισμοί που επιβάλλονται στους αριθμούς κάτω από τα πρόσημα των ριζών (a≥0 κ.λπ.). Η αγνόησή τους μπορεί να προκαλέσει λανθασμένα αποτελέσματα. Για παράδειγμα, γνωρίζουμε ότι η ιδιότητα ισχύει για μη αρνητικό a . Με βάση αυτό, μπορούμε εύκολα να μετακινηθούμε, για παράδειγμα, από το σε, αφού το 8 είναι θετικός αριθμός. Αλλά αν πάρουμε μια σημαντική ρίζα ενός αρνητικού αριθμού, για παράδειγμα, και, με βάση την ιδιότητα που υποδεικνύεται παραπάνω, την αντικαταστήσουμε με , τότε στην πραγματικότητα αντικαθιστούμε το −2 με 2. Πράγματι, αχ. Δηλαδή, για το αρνητικό α η ισότητα μπορεί να είναι λανθασμένη, όπως και άλλες ιδιότητες των ριζών μπορεί να είναι λανθασμένες χωρίς να λαμβάνονται υπόψη οι προϋποθέσεις που καθορίζονται για αυτές.

Αλλά αυτό που ειπώθηκε στην προηγούμενη παράγραφο δεν σημαίνει καθόλου ότι εκφράσεις με αρνητικούς αριθμούς κάτω από τα πρόσημα των ριζών δεν μπορούν να μετασχηματιστούν χρησιμοποιώντας τις ιδιότητες των ριζών. Απλώς πρέπει να «προετοιμαστούν» πρώτα εφαρμόζοντας τους κανόνες για τη λειτουργία με αριθμούς ή χρησιμοποιώντας τον ορισμό μιας περιττής ρίζας ενός αρνητικού αριθμού, που αντιστοιχεί στην ισότητα , όπου −a είναι ένας αρνητικός αριθμός (ενώ το a είναι θετικό). Για παράδειγμα, δεν μπορεί να αντικατασταθεί αμέσως από , καθώς οι −2 και −3 είναι αρνητικοί αριθμοί, αλλά μας επιτρέπει να μετακινηθούμε από τη ρίζα στο , και στη συνέχεια να εφαρμόσουμε περαιτέρω την ιδιότητα της ρίζας ενός προϊόντος: . Και σε ένα από τα προηγούμενα παραδείγματα, ήταν απαραίτητο να μετακινηθείτε από τη ρίζα στη ρίζα της δέκατης όγδοης δύναμης όχι έτσι, αλλά έτσι .

Έτσι, για να μετατρέψετε εκφράσεις χρησιμοποιώντας τις ιδιότητες των ριζών, χρειάζεστε

• επιλέξτε την κατάλληλη ιδιότητα από τη λίστα,
• βεβαιωθείτε ότι οι αριθμοί κάτω από τη ρίζα ικανοποιούν τις προϋποθέσεις για την επιλεγμένη ιδιότητα (διαφορετικά θα πρέπει να πραγματοποιήσετε προκαταρκτικούς μετασχηματισμούς),
• και πραγματοποιήστε τον επιδιωκόμενο μετασχηματισμό.

Μετατροπή εκφράσεων με μεταβλητές κάτω από ριζικά πρόσημα

Για να μετασχηματίσετε παράλογες εκφράσεις που περιέχουν όχι μόνο αριθμούς αλλά και μεταβλητές κάτω από το σύμβολο της ρίζας, οι ιδιότητες των ριζών που αναφέρονται στην πρώτη παράγραφο αυτού του άρθρου πρέπει να εφαρμοστούν προσεκτικά. Αυτό οφείλεται κυρίως στις προϋποθέσεις που πρέπει να πληρούν οι αριθμοί που περιλαμβάνονται στους τύπους. Για παράδειγμα, με βάση τον τύπο, η παράσταση μπορεί να αντικατασταθεί από μια παράσταση μόνο για εκείνες τις τιμές του x που ικανοποιούν τις συνθήκες x≥0 και x+1≥0, αφού ο καθορισμένος τύπος καθορίζεται για a≥0 και b ≥0.

Ποιοι είναι οι κίνδυνοι από την παράβλεψη αυτών των συνθηκών; Η απάντηση σε αυτό το ερώτημα καταδεικνύεται ξεκάθαρα από το ακόλουθο παράδειγμα. Ας υποθέσουμε ότι πρέπει να υπολογίσουμε την τιμή μιας παράστασης στο x=−2. Αν αντικαταστήσουμε αμέσως τον αριθμό −2 αντί της μεταβλητής x, θα πάρουμε την τιμή που χρειαζόμαστε . Τώρα ας φανταστούμε ότι, με βάση ορισμένες εκτιμήσεις, μετατρέψαμε τη δεδομένη έκφραση στη μορφή , και μόνο μετά από αυτό αποφασίσαμε να υπολογίσουμε την τιμή. Αντικαθιστούμε τον αριθμό −2 με το x και καταλήγουμε στην παράσταση , που δεν βγάζει νόημα.

Ας δούμε τι συμβαίνει με το εύρος των επιτρεπόμενων τιμών (APV) της μεταβλητής x κατά τη μετάβαση από έκφραση σε έκφραση. Δεν ήταν τυχαίο που αναφέραμε το ODZ, καθώς αυτό είναι ένα σοβαρό εργαλείο για την παρακολούθηση του παραδεκτού των μετασχηματισμών που έγιναν, και μια αλλαγή στο ODZ μετά τη μετατροπή μιας έκφρασης θα πρέπει, τουλάχιστον, να σηκώνει κόκκινες σημαίες. Η εύρεση του ODZ για αυτές τις εκφράσεις δεν είναι δύσκολη. Για την έκφραση της ODZ προσδιορίζεται από την ανισότητα x·(x+1)≥0, η λύση της δίνει σύνολο αριθμών (−∞, −1]∪∪∪}