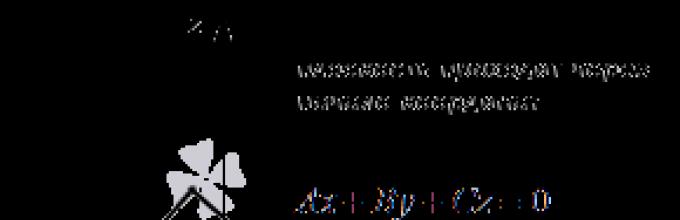
Εάν όλοι οι αριθμοί A, B, C και D είναι μη μηδενικοί, τότε καλείται η γενική εξίσωση του επιπέδου πλήρης... Διαφορετικά, καλείται η γενική εξίσωση του επιπέδου ατελής.

Εξετάστε όλα τα πιθανά κοινά ελλιπείς εξισώσεις επίπεδα σε ένα ορθογώνιο σύστημα συντεταγμένων Oxyz σε τρισδιάστατο χώρο.

Ας D \u003d 0, τότε έχουμε μια γενική ατελή εξίσωση του επιπέδου της φόρμας. Αυτό το επίπεδο στο ορθογώνιο σύστημα συντεταγμένων Oxyz διέρχεται από την προέλευση. Πράγματι, όταν αντικαθιστούμε τις συντεταγμένες ενός σημείου στην προκύπτουσα ελλιπή εξίσωση του επιπέδου, φτάνουμε σε μια ταυτότητα.


Σε, ή, ή έχουμε γενικές ατελείς εξισώσεις των επιπέδων, ή, ή, αντίστοιχα. Αυτές οι εξισώσεις ορίζουν επίπεδα παράλληλα με τα επίπεδα συντεταγμένων Oxy, Oxz και Oyz, αντίστοιχα (δείτε το άρθρο σχετικά με την κατάσταση του παραλληλισμού των επιπέδων) και περνώντας από τα σημεία και αντίστοιχα. Πότε. Από το σημείο ανήκει στο επίπεδο από συνθήκη, τότε οι συντεταγμένες αυτού του σημείου πρέπει να ικανοποιούν την εξίσωση του επιπέδου, δηλαδή, η ισότητα πρέπει να ισχύει. Από εδώ βρίσκουμε. Έτσι, η απαιτούμενη εξίσωση έχει τη μορφή.

Εδώ είναι ένας δεύτερος τρόπος επίλυσης αυτού του προβλήματος.

Δεδομένου ότι το επίπεδο, η γενική εξίσωση της οποίας πρέπει να συνθέσουμε, είναι παράλληλη με το επίπεδο Oyz, τότε ο κανονικός φορέας του επιπέδου Oyz μπορεί να ληφθεί ως ο φυσικός του φορέας. Ο κανονικός φορέας του επιπέδου συντεταγμένων Oyz είναι ο φορέας συντεταγμένων. Τώρα γνωρίζουμε τον κανονικό φορέα του επιπέδου και το σημείο του επιπέδου, επομένως, μπορούμε να καταγράψουμε τη γενική εξίσωσή του (λύσαμε ένα παρόμοιο πρόβλημα στην προηγούμενη παράγραφο αυτού του άρθρου):
, τότε οι συντεταγμένες του πρέπει να ικανοποιούν την εξίσωση του επιπέδου. Επομένως, η ισότητα όπου βρίσκουμε. Τώρα μπορούμε να γράψουμε την επιθυμητή γενική εξίσωση του επιπέδου, έχει τη μορφή.

Απάντηση:

Λίστα αναφορών.

  • Bugrov Y.S., Nikolsky S.M. Ανώτερα μαθηματικά. Τόμος 1: στοιχεία γραμμική άλγεβρα και αναλυτική γεωμετρία.
  • Ilyin V.A., Poznyak E.G. Αναλυτική γεωμετρία.

Μπορείτε να το ρυθμίσετε με διαφορετικούς τρόπους (ένα σημείο και ένα διάνυσμα, δύο σημεία και ένα διάνυσμα, τρία σημεία κ.λπ.). Με αυτό κατά νου, η εξίσωση του επιπέδου μπορεί να έχει διάφορες μορφές. Επίσης, εάν πληρούνται ορισμένες προϋποθέσεις, τα επίπεδα μπορεί να είναι παράλληλα, κάθετα, τέμνοντα κ.λπ. Θα μιλήσουμε για αυτό σε αυτό το άρθρο. Θα μάθουμε πώς να σχεδιάζουμε τη γενική εξίσωση του αεροπλάνου και πολλά άλλα.

Κανονική μορφή της εξίσωσης

Ας υποθέσουμε ότι υπάρχει ένας χώρος R 3 που έχει ένα ορθογώνιο σύστημα συντεταγμένων XYZ. Ας ορίσουμε ένα διάνυσμα α, το οποίο θα απελευθερωθεί από το αρχικό σημείο Ο. Μέσα από το τέλος του διανύσματος α, σχεδιάστε ένα επίπεδο P, το οποίο θα είναι κάθετο σε αυτό.

Υποδηλώνουμε σε ένα αυθαίρετο σημείο Q \u003d (x, y, z). Ας υπογράψουμε το διάνυσμα ακτίνας του σημείου Q με το γράμμα p. Σε αυτήν την περίπτωση, το μήκος του φορέα α είναι ίσο με p \u003d Ια και Ι \u003d (cosα, cosβ, cosγ).

Αυτός είναι ένας φορέας μονάδας, ο οποίος κατευθύνεται προς τα πλάγια, όπως ο φορέας α. Τα α, β και γ είναι οι γωνίες που σχηματίζονται μεταξύ του διανύσματος Ʋ και των θετικών κατευθύνσεων των διαστημικών αξόνων x, y, z, αντίστοιχα. Η προβολή οποιουδήποτε σημείου QϵП στο διάνυσμα Ʋ \u200b\u200bείναι μια σταθερή τιμή, η οποία είναι ίση με p: (p, Ʋ) \u003d p (p \u003d0).

Η παραπάνω εξίσωση έχει νόημα όταν p \u003d 0. Το μόνο πράγμα είναι ότι το επίπεδο P σε αυτήν την περίπτωση θα τέμνει το σημείο O (α \u003d 0), το οποίο είναι η προέλευση, και το διάνυσμα μονάδας Ʋ που εκδίδεται από το σημείο O θα είναι κάθετο προς το P, παρά την κατεύθυνσή του, που σημαίνει ότι ο φορέας Ʋ καθορίζεται με ακριβής στο σημείο. Η προηγούμενη εξίσωση είναι η εξίσωση του επιπέδου μας P, που εκφράζεται σε διανυσματική μορφή. Αλλά σε συντεταγμένες, θα μοιάζει με αυτό:

Το P εδώ είναι μεγαλύτερο από ή ίσο με 0. Βρήκαμε την εξίσωση του επιπέδου στο διάστημα σε κανονική μορφή.

Γενική εξίσωση

Εάν πολλαπλασιάσουμε την εξίσωση σε συντεταγμένες με οποιονδήποτε αριθμό που δεν είναι μηδέν, λαμβάνουμε μια εξίσωση που είναι ισοδύναμη με τη δεδομένη, η οποία ορίζει το ίδιο επίπεδο. Θα μοιάζει με αυτό:

Εδώ τα A, B, C είναι αριθμοί που είναι ταυτόχρονα μηδενικοί. Αυτή η εξίσωση αναφέρεται ως η γενική εξίσωση επιπέδου.

Εξισώσεις αεροπλάνων. Ειδικές περιπτώσεις

Η εξίσωση σε γενική μορφή μπορεί να τροποποιηθεί παρουσία πρόσθετες προϋποθέσεις... Ας εξετάσουμε μερικά από αυτά.

Ας υποθέσουμε ότι ο συντελεστής Α είναι ίσος με 0. Αυτό σημαίνει ότι αυτό το επίπεδο είναι παράλληλο με τον δεδομένο άξονα Οξ. Σε αυτήν την περίπτωση, η μορφή της εξίσωσης θα αλλάξει: Vu + Cz + D \u003d 0.

Ομοίως, η μορφή της εξίσωσης θα αλλάξει υπό τις ακόλουθες συνθήκες:

  • Πρώτον, εάν B \u003d 0, τότε η εξίσωση θα αλλάξει σε Ax + Cz + D \u003d 0, η οποία θα δείχνει ότι είναι παράλληλη με τον άξονα Oy.
  • Δεύτερον, εάν C \u003d 0, τότε η εξίσωση μετατρέπεται σε Ax + Vy + D \u003d 0, το οποίο θα μιλά για παραλληλισμό με τον δεδομένο άξονα Oz.
  • Τρίτον, αν D \u003d 0, η εξίσωση θα μοιάζει με Ax + Vy + Cz \u003d 0, που σημαίνει ότι το επίπεδο τέμνει το O (προέλευση).
  • Τέταρτον, εάν A \u003d B \u003d 0, τότε η εξίσωση θα αλλάξει σε Cz + D \u003d 0, η οποία θα αποδειχθεί παράλληλη με το Oxy.
  • Πέμπτον, εάν B \u003d C \u003d 0, τότε η εξίσωση γίνεται Ax + D \u003d 0, που σημαίνει ότι το επίπεδο προς το Oyz είναι παράλληλο.
  • Έκτον, εάν A \u003d C \u003d 0, τότε η εξίσωση θα έχει τη μορφή Vy + D \u003d 0, δηλαδή θα αναφέρει τον παραλληλισμό στην Oxz.

Προβολή εξίσωσης σε τμήματα

Στην περίπτωση που οι αριθμοί A, B, C, D είναι διαφορετικοί από το μηδέν, η μορφή εξίσωσης (0) μπορεί να έχει ως εξής:

x / a + y / b + z / c \u003d 1,

στο οποίο a \u003d -D / A, b \u003d -D / B, c \u003d -D / C.

Φτάνουμε στο τέλος Αξίζει να σημειωθεί ότι αυτό το επίπεδο θα τέμνει τον άξονα Ox σε ένα σημείο με συντεταγμένες (a, 0,0), Oy - (0, b, 0) και Oz - (0,0, c).

Λαμβάνοντας υπόψη την εξίσωση x / a + y / b + z / c \u003d 1, είναι εύκολο να απεικονιστεί οπτικά η θέση του επιπέδου σε σχέση με ένα δεδομένο σύστημα συντεταγμένων.

Συντεταγμένες κανονικού διανύσματος

Το κανονικό διάνυσμα n στο επίπεδο P έχει συντεταγμένες που είναι οι συντελεστές της γενικής εξίσωσης αυτού του επιπέδου, δηλαδή, n (A, B, C).

Προκειμένου να προσδιοριστούν οι συντεταγμένες του κανονικού n, αρκεί να γνωρίζουμε τη γενική εξίσωση του δεδομένου επιπέδου.

Όταν χρησιμοποιείτε την εξίσωση σε τμήματα, η οποία έχει τη μορφή x / a + y / b + z / c \u003d 1, όπως και με τη γενική εξίσωση, μπορείτε να γράψετε τις συντεταγμένες οποιουδήποτε κανονικού διανύσματος ενός δεδομένου επιπέδου: (1 / a + 1 / b + 1 / από).

Πρέπει να σημειωθεί ότι ο κανονικός φορέας βοηθά στην επίλυση διαφόρων προβλημάτων. Τα πιο συνηθισμένα προβλήματα περιλαμβάνουν το πρόβλημα απόδειξης της κάθετης ή παραλληλισμού των επιπέδων, το πρόβλημα εύρεσης των γωνιών μεταξύ επιπέδων ή γωνιών μεταξύ επιπέδων και γραμμών.

Προβολή της εξίσωσης του επιπέδου σύμφωνα με τις συντεταγμένες του σημείου και του κανονικού διανύσματος

Ένας μη μηδενικός φορέας n κάθετος σε ένα δεδομένο επίπεδο ονομάζεται κανονικός (κανονικός) για ένα δεδομένο επίπεδο.

Ας υποθέσουμε ότι στο συντονισμός χώρου (ορθογώνιο σύστημα συντεταγμένων) Oxyz δίνονται:

  • σημείο Мₒ με συντεταγμένες (xₒ, yₒ, zₒ);
  • μηδέν διάνυσμα n \u003d A * i + B * j + C * k.

Είναι απαραίτητο να καταρτιστεί μια εξίσωση για ένα επίπεδο που θα διέρχεται από το σημείο Mₒ κάθετα προς το κανονικό n.

Στο διάστημα, επιλέξτε οποιοδήποτε αυθαίρετο σημείο και δηλώστε το με M (x y, z). Αφήστε το διάνυσμα ακτίνας οποιουδήποτε σημείου M (x, y, z) να είναι r \u003d x * i + y * j + z * k και το διάνυσμα ακτίνας του σημείου Mₒ (xₒ, yₒ, zₒ) - rₒ \u003d xₒ * i + yₒ * j + zₒ * k. Το σημείο M θα ανήκει σε ένα δεδομένο επίπεδο εάν το διάνυσμα МₒМ είναι κάθετο προς το διάνυσμα n. Ας γράψουμε την κατάσταση ορθογωνικότητας χρησιμοποιώντας το προϊόν κουκκίδων:

[МₒМ, n] \u003d 0.

Δεδομένου ότι МₒМ \u003d r-rₒ, η διανυσματική εξίσωση του επιπέδου θα μοιάζει με αυτό:

Αυτή η εξίσωση μπορεί να έχει άλλη μορφή. Για αυτό, χρησιμοποιούνται οι ιδιότητες του προϊόντος κουκκίδων και μεταμορφώνεται η αριστερή πλευρά της εξίσωσης. \u003d -. Εάν το δηλώσουμε ως c, τότε έχουμε την ακόλουθη εξίσωση: - c \u003d 0 ή \u003d c, η οποία εκφράζει τη σταθερότητα των προβολών στον κανονικό φορέα διανυσμάτων ακτίνας δεδομένων σημείων που ανήκουν στο επίπεδο.

Τώρα μπορείτε να λάβετε τη μορφή συντεταγμένης γραφής της διανυσματικής εξίσωσης του επιπέδου μας \u003d 0. Δεδομένου r-rₒ \u003d (x-xₒ) * i + (y-yₒ) * j + (z-zₒ) * k, και n \u003d A * i + B * j + C * k, έχουμε:

Αποδεικνύεται ότι έχουμε μια εξίσωση ενός επιπέδου που διέρχεται από ένα σημείο κάθετο προς το κανονικό n:

A * (x- xₒ) + B * (y-yₒ) C * (z-zₒ) \u003d 0.

Η μορφή της εξίσωσης του επιπέδου σύμφωνα με τις συντεταγμένες δύο σημείων και ένα διάνυσμα γραμμικό στο επίπεδο

Ας ορίσουμε δύο αυθαίρετα σημεία M '(x', y ', z') και M ″ (x ″, y ″, z ″), καθώς και ένα διάνυσμα a (a ′, a ″, a).

Τώρα θα είμαστε σε θέση να καταρτίσουμε μια εξίσωση ενός δεδομένου επιπέδου, η οποία θα περάσει από τα υπάρχοντα σημεία M ′ και M ″, καθώς και οποιοδήποτε σημείο M με συντεταγμένες (x, y, z) παράλληλα με ένα δεδομένο διάνυσμα a.

Επιπλέον, τα διανύσματα M′M \u003d (x-x ′; y-y ′; zz ′) και M ″ M \u003d (x ″ -x ′; y ″ -y ′; z ″ -z ′) πρέπει να είναι ταυτόχρονα με το διάνυσμα a \u003d (a ′, a ″, a ‴), που σημαίνει ότι (M′M, M ″ M, a) \u003d 0.

Έτσι, η εξίσωση ενός αεροπλάνου στο διάστημα θα μοιάζει με αυτό:

Άποψη της εξίσωσης ενός αεροπλάνου που τέμνει τρία σημεία

Ας πούμε ότι έχουμε τρία σημεία: (x ′, y ′, z ′), (x ″, y ″, z ″), (x ‴, y ‴, z ‴), τα οποία δεν ανήκουν σε μία ευθεία γραμμή. Είναι απαραίτητο να γράψετε την εξίσωση του επιπέδου που διέρχεται από τα τρία σημεία που δίνονται. Η θεωρία της γεωμετρίας ισχυρίζεται ότι αυτό το είδος αεροπλάνου υπάρχει πραγματικά, μόνο είναι το μόνο και απαράμιλλο. Δεδομένου ότι αυτό το επίπεδο τέμνει το σημείο (x ′, y ′, z ′), η μορφή της εξίσωσης θα έχει ως εξής:

Εδώ τα A, B, C είναι μη μηδενικά ταυτόχρονα. Επίσης, το δεδομένο επίπεδο τέμνει δύο ακόμη σημεία: (x ″, y ″, z ″) και (x ‴, y ‴, z ‴). Ως προς αυτό, πρέπει να πληρούνται οι ακόλουθες προϋποθέσεις:

Τώρα μπορούμε να συνθέσουμε ένα ομοιογενές σύστημα με άγνωστα u, v, w:

Στο δικό μας περίπτωση x, y ή z είναι ένα αυθαίρετο σημείο που ικανοποιεί την εξίσωση (1). Λαμβάνοντας υπόψη την εξίσωση (1) και το σύστημα εξισώσεων (2) και (3), το σύστημα εξισώσεων που υποδεικνύεται στο παραπάνω σχήμα ικανοποιείται από τον φορέα N (A, B, C), ο οποίος είναι ασυνήθιστος. Αυτός είναι ο λόγος για τον οποίο ο καθοριστής αυτού του συστήματος είναι ίσος με το μηδέν.

Εξίσωση (1), την οποία έχουμε, αυτή είναι η εξίσωση του επιπέδου. Περνάει ακριβώς από 3 σημεία και είναι εύκολο να το ελέγξετε. Για να γίνει αυτό, πρέπει να επεκτείνουμε τον καθοριστικό μας παράγοντα με στοιχεία που βρίσκονται στην πρώτη γραμμή. Από τις υπάρχουσες ιδιότητες του καθοριστικού παράγοντα προκύπτει ότι το επίπεδο μας τέμνει ταυτόχρονα τρία αρχικά καθορισμένα σημεία (x ′, y ′, z ′), (x ″, y ″, z ″), (x ‴, y ‴, z ‴). Δηλαδή, έχουμε λύσει το έργο που έχει τεθεί μπροστά μας.

Γωνία γωνία μεταξύ επιπέδων

Η διεδρική γωνία είναι χωρική γεωμετρικό σχήμασχηματίζεται από δύο μισά επίπεδα που προέρχονται από μία ευθεία γραμμή. Με άλλα λόγια, αυτό είναι ένα μέρος του χώρου που περιορίζεται από αυτά τα μισά επίπεδα.

Ας πούμε ότι έχουμε δύο επίπεδα με τις ακόλουθες εξισώσεις:

Γνωρίζουμε ότι τα διανύσματα N \u003d (A, B, C) και N¹ \u003d (A¹, B¹, C¹) είναι κάθετα σύμφωνα με τα δεδομένα επίπεδα. Από την άποψη αυτή, η γωνία φ μεταξύ των διανυσμάτων Ν και Ν2 είναι ίση με τη γωνία (διεδρική), η οποία βρίσκεται μεταξύ αυτών των επιπέδων. Το κλιματικό προϊόν είναι:

NN¹ \u003d | N || N¹ | cos φ,

ακριβώς επειδή

cosφ \u003d NN¹ / | N || N¹ | \u003d (AA¹ + BB¹ + CC¹) / ((√ (A² + B² + C²)) * (√ (A¹) ² + (B¹) ² + (C¹) ²)).

Αρκεί να ληφθεί υπόψη ότι 0≤φ≤π.

Στην πραγματικότητα, τα δύο επίπεδα που τέμνονται σχηματίζουν δύο γωνίες (δίεδρο): φ 1 και φ 2. Το άθροισμά τους ισούται με π (φ 1 + φ 2 \u003d π). Όσον αφορά τα συνημίτητά τους, οι απόλυτες τιμές τους είναι ίσες, αλλά διαφέρουν ως προς τα σημάδια, δηλαδή, cos φ 1 \u003d -cos φ 2. Εάν στην εξίσωση (0) αντικαταστήσουμε τα A, B και C με τους αριθμούς -A, -B και -C, αντίστοιχα, τότε η εξίσωση που λαμβάνουμε θα καθορίσει το ίδιο επίπεδο, τη μόνη γωνία φ στην εξίσωση cos φ \u003d NN 1 / | Ν || Ν 1 | θα αντικατασταθεί από π-φ.

Κάθετη εξίσωση επιπέδου

Τα κάθετα επίπεδα είναι επίπεδα μεταξύ των οποίων η γωνία είναι 90 μοίρες. Χρησιμοποιώντας το υλικό που περιγράφεται παραπάνω, μπορούμε να βρούμε την εξίσωση ενός επιπέδου κάθετου προς ένα άλλο. Ας υποθέσουμε ότι έχουμε δύο επίπεδα: Ax + By + Cz + D \u003d 0 και A¹x + B¹y + C¹z + D \u003d 0. Μπορούμε να υποστηρίξουμε ότι θα είναι κάθετα εάν cosφ \u003d 0. Αυτό σημαίνει ότι NN¹ \u003d AA¹ + BB¹ + CC¹ \u003d 0.

Παράλληλη εξίσωση επιπέδου

Παράλληλα είναι δύο επίπεδα που δεν περιέχουν κοινά σημεία.

Η συνθήκη (οι εξισώσεις τους είναι ίδιες με την προηγούμενη παράγραφο) είναι ότι τα διανύσματα Ν και Ν2, που είναι κάθετα σε αυτά, είναι γραμμικά. Αυτό σημαίνει ότι πληρούνται οι ακόλουθες προϋποθέσεις αναλογικότητας:

A / A¹ \u003d B / B¹ \u003d C / C¹.

Εάν οι συνθήκες αναλογικότητας επεκταθούν - A / A¹ \u003d B / B¹ \u003d C / C¹ \u003d DD¹,

Αυτό δείχνει ότι τα αεροπλάνα συμπίπτουν. Αυτό σημαίνει ότι οι εξισώσεις Ax + By + Cz + D \u003d 0 και A¹x + B¹y + C¹z + D¹ \u003d 0 περιγράφουν ένα επίπεδο.

Απόσταση από αεροπλάνο από σημείο

Ας πούμε ότι έχουμε ένα επίπεδο P, το οποίο δίνεται από την εξίσωση (0). Είναι απαραίτητο να βρείτε την απόσταση από το σημείο με συντεταγμένες (xₒ, yₒ, zₒ) \u003d Qₒ. Για να το κάνετε αυτό, πρέπει να φέρετε την εξίσωση του επιπέδου P σε κανονική μορφή:

(p, v) \u003d p (p00).

Σε αυτήν την περίπτωση, ρ (x, y, z) είναι ο φορέας ακτίνας του σημείου μας Q, που βρίσκεται στο P, p είναι το μήκος του κάθετου P, το οποίο απελευθερώθηκε από το μηδέν σημείο, v είναι ο φορέας μονάδας, ο οποίος βρίσκεται στην κατεύθυνση a.

Η διαφορά ρ-ρº του διανύσματος ακτίνας κάποιου σημείου Q \u003d (x, y, z), που ανήκει στο P, καθώς και του διανύσματος ακτίνας ενός δεδομένου σημείου Q 0 \u003d (xₒ, yₒ, zₒ) είναι ένας τέτοιος φορέας του οποίου η απόλυτη τιμή v είναι ίση με την απόσταση d που μπορεί να βρεθεί από Q 0 \u003d (xₒ, yₒ, zₒ) έως П:

D \u003d | (ρ-ρ 0, v) |, αλλά

(ρ-ρ 0, v) \u003d (ρ, v) - (ρ 0, v) \u003d p- (ρ 0, v).

Έτσι αποδεικνύεται

d \u003d | (ρ 0, v) -p |.

Έτσι, θα βρούμε την απόλυτη τιμή της προκύπτουσας έκφρασης, δηλαδή την επιθυμητή d.

Χρησιμοποιώντας τη γλώσσα παραμέτρων, έχουμε το προφανές:

d \u003d | Axₒ + Byₒ + Czₒ | / √ (A² + B² + C²).

Αν ένα καθορισμένο σημείο Το Q 0 είναι στην άλλη πλευρά του επιπέδου P, όπως η προέλευση, τότε μεταξύ του διανύσματος ρ-ρ 0 και v είναι επομένως:

d \u003d - (ρ-ρ 0, v) \u003d (ρ 0, v) -p\u003e 0.

Στην περίπτωση που το σημείο Q 0 μαζί με την προέλευση βρίσκεται στην ίδια πλευρά του P, τότε η δημιουργημένη γωνία είναι οξεία, δηλαδή:

d \u003d (ρ-ρ 0, v) \u003d p - (ρ 0, v)\u003e 0.

Ως αποτέλεσμα, αποδεικνύεται ότι στην πρώτη περίπτωση (ρ 0, v)\u003e p, στη δεύτερη (ρ 0, v)<р.

Το εφαπτόμενο επίπεδο και η εξίσωση του

Το επίπεδο εφαπτόμενης προς την επιφάνεια στο σημείο εφαπτομένης Mº είναι το επίπεδο που περιέχει όλες τις πιθανές εφαπτόμενες προς τις καμπύλες που έλκονται από αυτό το σημείο στην επιφάνεια.

Με αυτήν τη μορφή εξίσωσης της επιφάνειας F (x, y, z) \u003d 0, η εξίσωση του εφαπτόμενου επιπέδου στο σημείο εφαπτομένης Mº (xº, yº, zº) θα μοιάζει με αυτό:

F x (xº, yº, zº) (x-xº) + F x (xº, yº, zº) (y-yº) + F x (xº, yº, zº) (z-zº) \u003d 0.

Εάν θέσουμε την επιφάνεια σε ρητή μορφή z \u003d f (x, y), τότε το εφαπτόμενο επίπεδο θα περιγραφεί από την εξίσωση:

z-zº \u003d f (xº, yº) (x- xº) + f (xº, yº) (y-yº).

Διασταύρωση δύο επιπέδων

Στο σύστημα συντεταγμένων (ορθογώνιο) βρίσκεται το Oxyz, δίνονται δύο επίπεδα P ′ και P,, τα οποία τέμνονται και δεν συμπίπτουν. Δεδομένου ότι οποιοδήποτε επίπεδο σε ένα ορθογώνιο σύστημα συντεταγμένων καθορίζεται από τη γενική εξίσωση, θα υποθέσουμε ότι τα P ′ και P ″ δίδονται από τις εξισώσεις Ax + B′y + C′z + D ′ \u003d 0 και A ″ x + B ″ y + C ″ z + D ″ \u003d 0. Σε αυτήν την περίπτωση, έχουμε το κανονικό n ′ (A ′, B ′, C ′) του επιπέδου P and και το κανονικό n ″ (A ″, B ″, C ″) του επιπέδου P ″. Δεδομένου ότι τα αεροπλάνα μας δεν είναι παράλληλα και δεν συμπίπτουν, αυτοί οι φορείς δεν είναι γραμμικοί. Χρησιμοποιώντας τη γλώσσα των μαθηματικών, μπορούμε να γράψουμε αυτήν την κατάσταση ως εξής: n ′ ≠ n ″ ↔ (A ′, B ′, C ′) ≠ (λ * A ″, λ * B ″, λ * C ″), λϵR. Αφήστε την ευθεία γραμμή που βρίσκεται στη διασταύρωση των P ′ και P ″ να συμβολίζεται με το γράμμα a, στην περίπτωση αυτή a \u003d P ′ ∩ P ″.

a είναι η γραμμή που αποτελείται από το σύνολο όλων των σημείων των (κοινών) επιπέδων P ′ και P ″. Αυτό σημαίνει ότι οι συντεταγμένες οποιουδήποτε σημείου που ανήκει στην ευθεία γραμμή a πρέπει ταυτόχρονα να ικανοποιούν τις εξισώσεις A'x + B'y + C'z + D '\u003d 0 και A ″ x + B ″ y + C ″ z + D ″ \u003d 0. Αυτό σημαίνει ότι οι συντεταγμένες του σημείου θα είναι μια συγκεκριμένη λύση του ακόλουθου συστήματος εξισώσεων:

Ως αποτέλεσμα, αποδεικνύεται ότι η (γενική) λύση αυτού του συστήματος εξισώσεων θα καθορίσει τις συντεταγμένες καθενός από τα σημεία της ευθείας γραμμής, η οποία θα λειτουργήσει ως σημείο τομής των P ′ και P ″, και θα καθορίσει την ευθεία γραμμή στο σύστημα συντεταγμένων Oxyz (ορθογώνιο) στο διάστημα

Ιδιότητες μιας ευθείας γραμμής στην Ευκλείδεια γεωμετρία.

Μπορείτε να σχεδιάσετε απεριόριστα πολλές ευθείες γραμμές σε οποιοδήποτε σημείο.

Μια απλή ευθεία γραμμή μπορεί να σχεδιαστεί μέσω οποιωνδήποτε δύο σημείων που δεν συμπίπτουν.

Δύο μη ευθυγραμμισμένες ευθείες γραμμές στο επίπεδο είτε τέμνονται σε ένα σημείο, είτε είναι

παράλληλη (ακολουθεί από την προηγούμενη).

Σε τρισδιάστατο χώρο, υπάρχουν τρεις επιλογές για τη σχετική θέση δύο ευθειών γραμμών:

  • ευθείες γραμμές τέμνουν?
  • οι ευθείες γραμμές είναι παράλληλες.
  • ευθείες γραμμές τέμνονται.

Ευθεία γραμμή - αλγεβρική καμπύλη της πρώτης τάξης: σε ένα καρτεσιανό σύστημα συντεταγμένων, μια ευθεία γραμμή

δίνεται στο επίπεδο με εξίσωση του πρώτου βαθμού (γραμμική εξίσωση).

Γενική εξίσωση της γραμμής.

Ορισμός... Οποιαδήποτε ευθεία γραμμή σε επίπεδο μπορεί να δοθεί με εξίσωση πρώτης τάξης

Ax + Wu + C \u003d 0,

με σταθερά Α, Β δεν ισούται με μηδέν ταυτόχρονα. Αυτή η εξίσωση πρώτης τάξης ονομάζεται κοινός

εξίσωση μιας ευθείας γραμμής. Ανάλογα με τις τιμές των σταθερών Α, Β και ΑΠΟ είναι δυνατές οι ακόλουθες ειδικές περιπτώσεις:

. C \u003d 0, A ≠ 0, B ≠ 0 - η ευθεία γραμμή διέρχεται από την προέλευση

. A \u003d 0, B ≠ 0, C ≠ 0 (Από + C \u003d 0)- ευθεία γραμμή παράλληλη προς τον άξονα Ω

. B \u003d 0, A ≠ 0, C ≠ 0 (Ax + C \u003d 0) - ευθεία γραμμή παράλληλη προς τον άξονα OU

. B \u003d C \u003d 0, A ≠ 0 - η ευθεία γραμμή συμπίπτει με τον άξονα OU

. A \u003d C \u003d 0, B ≠ 0 - η ευθεία γραμμή συμπίπτει με τον άξονα Ω

Η εξίσωση μιας ευθείας γραμμής μπορεί να αναπαρασταθεί σε διαφορετικές μορφές, ανάλογα με οποιαδήποτε δεδομένη

αρχικές συνθήκες.

Εξίσωση μιας ευθείας γραμμής κατά μήκος ενός σημείου και ενός κανονικού διανύσματος.

Ορισμός... Σε ένα καρτεσιανό ορθογώνιο σύστημα συντεταγμένων, ένας φορέας με συστατικά (A, B)

κάθετα προς την ευθεία γραμμή που δίνεται από την εξίσωση

Ax + Wu + C \u003d 0.

Παράδειγμα... Βρείτε την εξίσωση μιας ευθείας γραμμής που διέρχεται από ένα σημείο Α (1, 2) κάθετα προς το διάνυσμα (3, -1).

Απόφαση... Στα A \u003d 3 και B \u003d -1, συνθέτουμε την εξίσωση της ευθείας γραμμής: 3x - y + C \u003d 0. Για να βρούμε τον συντελεστή C

αντικαταστήστε στην προκύπτουσα έκφραση τις συντεταγμένες του δεδομένου σημείου A. Παίρνουμε: 3 - 2 + C \u003d 0, επομένως

C \u003d -1. Σύνολο: η απαιτούμενη εξίσωση: 3x - y - 1 \u003d 0.

Εξίσωση μιας ευθείας γραμμής που διέρχεται από δύο σημεία.

Αφήστε δύο βαθμούς στο διάστημα M 1 (x 1, y 1, z 1)και M2 (x 2, y 2, z 2), τότε ευθεία εξίσωση,

περνώντας από αυτά τα σημεία:

Εάν οποιοσδήποτε από τους παρονομαστές είναι μηδέν, ο αντίστοιχος αριθμητής θα πρέπει να ισούται με μηδέν. Επί

επίπεδο, η εξίσωση της ευθείας γραμμής που γράφτηκε παραπάνω απλοποιείται:

αν ένα x 1 ≠ x 2 και x \u003d x 1 , αν ένα x 1 \u003d x 2 .

Κλάσμα \u003d κ που ονομάζεται κλίση ευθεία.

Παράδειγμα... Βρείτε την εξίσωση της ευθείας γραμμής που διέρχεται από τα σημεία A (1, 2) και B (3, 4).

Απόφαση... Εφαρμόζοντας τον παραπάνω τύπο, λαμβάνουμε:

Εξίσωση ευθείας γραμμής κατά σημείο και κλίση.

Εάν η γενική εξίσωση της ευθείας γραμμής Ax + Wu + C \u003d 0 οδηγεί στη φόρμα:

και ορίστε , τότε η προκύπτουσα εξίσωση καλείται

εξίσωση μιας ευθείας γραμμής με κλίση k.

Εξίσωση μιας ευθείας γραμμής κατά μήκος ενός διανύσματος σημείου και κατεύθυνσης.

Αναλογικά με την παράγραφο που εξετάζει την εξίσωση μιας ευθείας γραμμής μέσω του κανονικού διανύσματος, μπορείτε να εισαγάγετε την εργασία

μια ευθεία γραμμή μέσω ενός σημείου και ενός φορέα κατεύθυνσης μιας ευθείας γραμμής.

Ορισμός... Κάθε μη μηδέν διάνυσμα (α 1, α 2)των οποίων τα συστατικά πληρούν την κατάσταση

Аα 1 + Вα 2 \u003d 0 που ονομάζεται Διεύθυνση φορέα μιας ευθείας γραμμής.

Ax + Wu + C \u003d 0.

Παράδειγμα... Βρείτε την εξίσωση μιας ευθείας γραμμής με ένα φορέα κατεύθυνσης (1, -1) και περνώντας από το σημείο A (1, 2).

Απόφαση... Η εξίσωση της επιθυμητής ευθείας γραμμής θα αναζητηθεί με τη μορφή: Ax + By + C \u003d 0. Σύμφωνα με τον ορισμό,

οι συντελεστές πρέπει να πληρούν τους όρους:

1 * A + (-1) * B \u003d 0, δηλ. Α \u003d Β.

Στη συνέχεια, η εξίσωση της ευθείας γραμμής έχει τη μορφή: Ax + Ay + C \u003d 0, ή x + y + C / A \u003d 0.

στο x \u003d 1, y \u003d 2παίρνουμε C / A \u003d -3, δηλ. απαιτούμενη εξίσωση:

x + y - 3 \u003d 0

Εξίσωση ευθείας γραμμής σε τμήματα.

Εάν στη γενική εξίσωση της ευθείας γραμμής Ax + Vy + C \u003d 0 C ≠ 0, τότε, διαιρώντας με -C, παίρνουμε:

ή πού

Η γεωμετρική έννοια των συντελεστών είναι ότι ο συντελεστής α είναι η συντεταγμένη του σημείου τομής

ευθεία με άξονα Ω, και σι - η συντεταγμένη του σημείου τομής της ευθείας γραμμής με τον άξονα OU.

Παράδειγμα... Δίνεται η γενική εξίσωση της γραμμής x - y + 1 \u003d 0.Βρείτε την εξίσωση αυτής της ευθείας γραμμής σε τμήματα.

C \u003d 1, a \u003d -1, b \u003d 1.

Κανονική εξίσωση μιας ευθείας γραμμής.

Εάν και οι δύο πλευρές της εξίσωσης Ax + Wu + C \u003d 0 διαιρέστε με τον αριθμό η οποία ονομάζεται

παράγοντας ομαλοποίησης, τότε παίρνουμε

xcosφ + ysinφ - p \u003d 0 -κανονική εξίσωση γραμμής.

Το σημείο ± του συντελεστή ομαλοποίησης πρέπει να επιλέγεται έτσι μ * Γ< 0.

Ρ - το μήκος της κάθετης πτώσης από την αρχή στην ευθεία γραμμή,

και φ - η γωνία που σχηματίζεται από αυτήν την κάθετη με τη θετική κατεύθυνση του άξονα Ω.

Παράδειγμα... Δίνεται η γενική εξίσωση της γραμμής 12x - 5y - 65 \u003d 0... Απαιτείται για τη σύνταξη διαφορετικών τύπων εξισώσεων

αυτή την ευθεία γραμμή.

Η εξίσωση αυτής της γραμμής σε τμήματα:

Εξίσωση αυτής της γραμμής με κλίση: (διαιρέστε με 5)

Εξίσωση ευθείας γραμμής:

cos φ \u003d 12/13; sin φ \u003d -5/13; p \u003d 5.

Πρέπει να σημειωθεί ότι δεν μπορεί να αντιπροσωπεύεται κάθε ευθεία γραμμή από μια εξίσωση σε τμήματα, για παράδειγμα, ευθείες γραμμές,

παράλληλα με τους άξονες ή διέρχεται από την προέλευση.

Η γωνία μεταξύ ευθειών γραμμών στο επίπεδο.

Ορισμός... Εάν δίνονται δύο γραμμές y \u003d k 1 x + b 1, y \u003d k 2 x + b 2 , τότε μια οξεία γωνία μεταξύ αυτών των γραμμών

θα οριστεί ως

Δύο ευθείες γραμμές είναι παράλληλες εάν k 1 \u003d k 2... Δύο ευθείες γραμμές είναι κάθετες,

αν ένα k 1 \u003d -1 / k 2 .

Θεώρημα.

Απευθείας Ax + Wu + C \u003d 0και A 1 x + B 1 y + C 1 \u003d 0 είναι παράλληλοι όταν οι συντελεστές είναι ανάλογοι

А 1 \u003d λА, В 1 \u003d λВ... Εάν επίσης С 1 \u003d λС, τότε οι ευθείες γραμμές συμπίπτουν. Συντεταγμένες του σημείου τομής δύο γραμμών

Βρίσκονται ως λύση στο σύστημα εξισώσεων αυτών των ευθειών.

Εξίσωση μιας ευθείας γραμμής που διέρχεται από ένα δεδομένο σημείο κάθετο προς μια δεδομένη ευθεία γραμμή.

Ορισμός... Γραμμή μέσω σημείου M 1 (x 1, y 1) και κάθετα στη γραμμή y \u003d kx + b

αντιπροσωπεύεται από την εξίσωση:

Απόσταση από σημείο σε γραμμή.

Θεώρημα... Εάν δοθεί ένα σημείο Μ (x 0, y 0), η απόσταση από την ευθεία γραμμή Ax + Wu + C \u003d 0οριζεται ως:

Απόδειξη... Αφήστε το θέμα M 1 (x 1, y 1) - η βάση της κάθετης πτώσης από το σημείο Μγια ένα δεδομένο

ευθεία. Στη συνέχεια, η απόσταση μεταξύ των σημείων Μκαι Μ 1:

(1)

Συντεταγμένες x 1 και στο 1 μπορεί να βρεθεί ως λύση στο σύστημα εξισώσεων:

Η δεύτερη εξίσωση του συστήματος είναι η εξίσωση μιας ευθείας γραμμής που διέρχεται από ένα δεδομένο σημείο Μ 0 κάθετο προς

μια δεδομένη ευθεία γραμμή. Εάν μετατρέψουμε την πρώτη εξίσωση του συστήματος στη μορφή:

A (x - x 0) + B (y - y 0) + Ax 0 + Από 0 + C \u003d 0,

τότε, λύνοντας, παίρνουμε:

Αντικαθιστώντας αυτές τις εκφράσεις σε εξίσωση (1), βρίσκουμε:

Το θεώρημα αποδεικνύεται.

Προκειμένου να τραβηχτεί ένα μόνο επίπεδο μέσω τριών σημείων στο διάστημα, είναι απαραίτητο αυτά τα σημεία να μην βρίσκονται σε μία ευθεία γραμμή.

Εξετάστε τα σημεία M 1 (x 1, y 1, z 1), M 2 (x 2, y 2, z 2), M 3 (x 3, y 3, z 3) σε ένα κοινό καρτεσιανό σύστημα συντεταγμένων.

Προκειμένου ένα αυθαίρετο σημείο M (x, y, z) να βρίσκεται στο ίδιο επίπεδο με τα σημεία M 1, M 2, M 3, τα διανύσματα πρέπει να είναι συμπαγή.

(
) = 0

Με αυτόν τον τρόπο,

Εξίσωση αεροπλάνου που διέρχεται από τρία σημεία:

Εξίσωση ενός επιπέδου σε δύο σημεία και ενός διανύσματος γραμμική στο επίπεδο.

Αφήστε τα σημεία M 1 (x 1, y 1, z 1), M 2 (x 2, y 2, z 2) και το διάνυσμα
.

Ας συνθέσουμε την εξίσωση του επιπέδου που διέρχεται από τα δεδομένα σημεία M 1 και M 2 και ένα αυθαίρετο σημείο M (x, y, z) παράλληλα με το διάνυσμα .

Διανύσματα
και διάνυσμα
πρέπει να είναι συμπαγής, δηλαδή

(
) = 0

Εξίσωση αεροπλάνου:

Εξίσωση του επιπέδου με ένα σημείο και δύο διανύσματα,

γραμμική στο αεροπλάνο.

Αφήστε δύο διανύσματα
και
, γραμμικά επίπεδα. Στη συνέχεια, για ένα αυθαίρετο σημείο M (x, y, z) που ανήκει στο επίπεδο, τα διανύσματα
πρέπει να είναι συμπαγής.

Εξίσωση αεροπλάνου:

Εξίσωση ενός επιπέδου με ένα σημείο και ένα κανονικό διάνυσμα .

Θεώρημα. Εάν ένα σημείο M δίνεται στο διάστημα 0 (Χ 0 , στις 0 , ζ 0 ), τότε η εξίσωση του επιπέδου που διέρχεται από το σημείο Μ 0 κάθετα προς το κανονικό διάνυσμα (ΕΝΑ, σι, ντο) έχει τη μορφή:

ΕΝΑ(Χ – Χ 0 ) + σι(γ – γ 0 ) + ντο(ζ – ζ 0 ) = 0.

Απόδειξη. Για ένα αυθαίρετο σημείο M (x, y, z) που ανήκει στο επίπεδο, συνθέτουμε ένα διάνυσμα. Επειδή διάνυσμα είναι ο κανονικός φορέας, τότε είναι κάθετος στο επίπεδο και, επομένως, είναι κάθετος προς το φορέα
... Στη συνέχεια, το προϊόν κουκκίδων

= 0

Έτσι, λαμβάνουμε την εξίσωση του επιπέδου

Το θεώρημα αποδεικνύεται.

Εξίσωση του επιπέδου σε τμήματα.

Εάν στη γενική εξίσωση Ax + Vy + Cz + D \u003d 0 διαιρέστε και τις δύο πλευρές με (-D)

,

αντικατάσταση
, έχουμε την εξίσωση του επιπέδου σε τμήματα:

Οι αριθμοί a, b, c είναι τα σημεία τομής του επιπέδου με τους άξονες x, y, z, αντίστοιχα.

Επίπεδο εξίσωσης σε διανυσματική μορφή.

Οπου

- διάνυσμα ακτίνας του τρέχοντος σημείου M (x, y, z),

Ένας φορέας μονάδας με την κατεύθυνση της κάθετης πέφτει πάνω στο επίπεδο από την προέλευση.

,  και  - γωνίες που σχηματίζονται από αυτόν τον φορέα με άξονες x, y, z.

p είναι το μήκος αυτής της κάθετης.

Σε συντεταγμένες, αυτή η εξίσωση έχει τη μορφή:

xcos + ycos + zcos - p \u003d 0.

Απόσταση από σημείο σε αεροπλάνο.

Η απόσταση από ένα αυθαίρετο σημείο M 0 (x 0, y 0, z 0) έως το επίπεδο Ax + Vy + Cz + D \u003d 0 είναι ίση με:

Παράδειγμα. Βρείτε την εξίσωση του επιπέδου, γνωρίζοντας ότι το σημείο P (4; -3; 12) είναι η βάση της κάθετης πτώσης από την προέλευση προς αυτό το επίπεδο.

Έτσι, Α \u003d 4/13; Β \u003d -3/13; C \u003d 12/13, ας χρησιμοποιήσουμε τον τύπο:

A (x - x) 0 ) + B (ε - ε 0 ) + C (z - z 0 ) = 0.

Παράδειγμα. Βρείτε την εξίσωση του επιπέδου που διέρχεται από δύο σημεία P (2; 0; -1) και

Q (1; -1; 3) κάθετα στο επίπεδο 3x + 2y - z + 5 \u003d 0.

Κανονικό διάνυσμα στο επίπεδο 3x + 2y - z + 5 \u003d 0
παράλληλα με το επιθυμητό επίπεδο.

Παίρνουμε:

Παράδειγμα. Βρείτε την εξίσωση του επιπέδου που διέρχεται από τα σημεία A (2, -1, 4) και

Σε (3, 2, -1) κάθετα στο επίπεδο Χ + στο + 2ζ – 3 = 0.

Η επιθυμητή εξίσωση του επιπέδου είναι: Α Χ + Β γ + Γ ζ + D \u003d 0, το κανονικό διάνυσμα σε αυτό το επίπεδο (Α, Β, Γ). Διάνυσμα
(1, 3, -5) ανήκει στο αεροπλάνο. Το επίπεδο που μας δίνεται, κάθετο προς το επιθυμητό, \u200b\u200bέχει κανονικό φορέα (1, 1, 2). Επειδή Τα σημεία Α και Β ανήκουν και στα δύο επίπεδα, και τότε τα επίπεδα είναι αμοιβαία κάθετα

Έτσι, ο κανονικός φορέας (11, -7, -2). Επειδή Το σημείο Α ανήκει στο επιθυμητό επίπεδο, τότε οι συντεταγμένες του πρέπει να ικανοποιούν την εξίσωση αυτού του επιπέδου, δηλαδή 112 + 71 - 24 + D \u003d 0; D \u003d -21.

Έχουμε λοιπόν την εξίσωση του επιπέδου: 11 Χ - 7γ – 2ζ – 21 = 0.

Παράδειγμα. Βρείτε την εξίσωση του επιπέδου, γνωρίζοντας ότι το σημείο P (4, -3, 12) είναι η βάση της κάθετης πτώσης από την προέλευση προς αυτό το επίπεδο.

Βρείτε τις συντεταγμένες του κανονικού διανύσματος
\u003d (4, -3, 12). Η επιθυμητή εξίσωση του επιπέδου είναι: 4 Χ – 3γ + 12ζ + D \u003d 0. Για να βρούμε τον συντελεστή D, αντικαθιστούμε τις συντεταγμένες του σημείου P στην εξίσωση:

16 + 9 + 144 + D \u003d 0

Λοιπόν, έχουμε την απαιτούμενη εξίσωση: 4 Χ – 3γ + 12ζ – 169 = 0

Παράδειγμα. Οι συντεταγμένες των κορυφών της πυραμίδας A 1 (1; 0; 3), A 2 (2; -1; 3), A 3 (2; 1; 1),

    Βρείτε το μήκος της άκρης A 1 A 2.

    Βρείτε τη γωνία μεταξύ των άκρων A 1 A 2 και A 1 A 4.

    Βρείτε τη γωνία μεταξύ της άκρης A 1 A 4 και της όψης A 1 A 2 A 3.

Αρχικά, βρείτε το κανονικό διάνυσμα στο πρόσωπο А 1 А 2 А 3 ως το διανυσματικό προϊόν των διανυσμάτων
και
.

= (2-1; 1-0; 1-3) = (1; 1; -2);

Βρείτε τη γωνία μεταξύ του κανονικού διανύσματος και του διανύσματος
.

-4 – 4 = -8.

Η ζητούμενη γωνία  μεταξύ του διανύσματος και του επιπέδου θα είναι  \u003d 90 0 - .

    Βρείτε την περιοχή του προσώπου A 1 A 2 A 3.

    Βρείτε τον όγκο της πυραμίδας.

    Βρείτε την εξίσωση του επιπέδου A 1 A 2 A 3.

Ας χρησιμοποιήσουμε τον τύπο για την εξίσωση ενός αεροπλάνου που διέρχεται από τρία σημεία.

2x + 2y + 2z - 8 \u003d 0

x + y + z - 4 \u003d 0;

Όταν χρησιμοποιείτε την έκδοση υπολογιστή " Ανώτερο μάθημα μαθηματικώνΜπορείτε να εκτελέσετε ένα πρόγραμμα που θα λύσει το παραπάνω παράδειγμα για τυχόν συντεταγμένες των κορυφών της πυραμίδας.

Για να ξεκινήσετε το πρόγραμμα, κάντε διπλό κλικ στο εικονίδιο:

Στο παράθυρο προγράμματος που ανοίγει, εισαγάγετε τις συντεταγμένες των κορυφών της πυραμίδας και πατήστε Enter. Έτσι, όλα τα σημεία απόφασης μπορούν να ληφθούν με τη σειρά.

Σημείωση: Για να εκτελέσετε το πρόγραμμα, πρέπει να έχετε εγκαταστήσει το λογισμικό Maple ( Waterloo Maple Inc.) οποιασδήποτε έκδοσης ξεκινώντας από το MapleV Release 4 στον υπολογιστή σας.