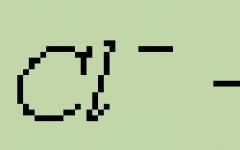Άρα, έχουμε δυνάμεις δύο. Εάν πάρετε τον αριθμό από την κάτω γραμμή, τότε μπορείτε εύκολα να βρείτε τη δύναμη στην οποία πρέπει να σηκώσετε δύο για να λάβετε αυτόν τον αριθμό. Για παράδειγμα, για να πάρετε 16, πρέπει να αυξήσετε δύο στην τέταρτη δύναμη. Και για να πάρετε 64, πρέπει να αυξήσετε δύο στην έκτη δύναμη. Αυτό φαίνεται από τον πίνακα.
Και τώρα - στην πραγματικότητα, ο ορισμός του λογάριθμου:
Η βάση ενός λογάριθμου του ορίσματος x είναι η ισχύς στην οποία πρέπει να αυξηθεί ο αριθμός a για να ληφθεί ο αριθμός x.
Σημείωση: log a x \u003d b, όπου a είναι η βάση, x είναι το όρισμα, b είναι στην πραγματικότητα αυτό με το οποίο ισούται ο λογάριθμος.
Για παράδειγμα, 2 3 = 8 ⇒ log 2 8 = 3 (ο λογάριθμος βάσης 2 του 8 είναι τρεις επειδή 2 3 = 8). Μπορεί επίσης να καταγράψει 2 64 = 6, αφού 2 6 = 64.
Η πράξη εύρεσης του λογάριθμου ενός αριθμού σε μια δεδομένη βάση ονομάζεται λογάριθμος. Ας προσθέσουμε λοιπόν μια νέα σειρά στον πίνακά μας:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| ημερολόγιο 2 2 = 1 | ημερολόγιο 2 4 = 2 | ημερολόγιο 2 8 = 3 | ημερολόγιο 2 16 = 4 | ημερολόγιο 2 32 = 5 | ημερολόγιο 2 64 = 6 |
Δυστυχώς, δεν εξετάζονται όλοι οι λογάριθμοι τόσο εύκολα. Για παράδειγμα, προσπαθήστε να βρείτε το αρχείο καταγραφής 2 5. Ο αριθμός 5 δεν βρίσκεται στον πίνακα, αλλά η λογική υπαγορεύει ότι ο λογάριθμος θα βρίσκεται κάπου στο τμήμα. Επειδή 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
Τέτοιοι αριθμοί ονομάζονται παράλογοι: οι αριθμοί μετά την υποδιαστολή μπορούν να γραφτούν επ' αόριστον και δεν επαναλαμβάνονται ποτέ. Εάν ο λογάριθμος αποδειχθεί παράλογος, είναι καλύτερα να τον αφήσετε ως εξής: log 2 5, log 3 8, log 5 100.
Είναι σημαντικό να κατανοήσουμε ότι ο λογάριθμος είναι μια έκφραση με δύο μεταβλητές (βάση και όρισμα). Στην αρχή, πολλοί άνθρωποι μπερδεύουν πού είναι η βάση και πού είναι το επιχείρημα. Για να αποφύγετε ενοχλητικές παρεξηγήσεις, απλά ρίξτε μια ματιά στην εικόνα:
[λεζάντα εικόνας]
Μπροστά μας δεν υπάρχει τίποτα άλλο από τον ορισμό του λογάριθμου. Θυμάμαι: ο λογάριθμος είναι η δύναμη, στο οποίο πρέπει να ανεβάσετε τη βάση για να λάβετε το επιχείρημα. Είναι η βάση που ανυψώνεται σε δύναμη - στην εικόνα επισημαίνεται με κόκκινο χρώμα. Αποδεικνύεται ότι η βάση είναι πάντα στο κάτω μέρος! Λέω αυτόν τον υπέροχο κανόνα στους μαθητές μου στο πρώτο μάθημα - και δεν υπάρχει σύγχυση.
Καταλάβαμε τον ορισμό - μένει να μάθουμε πώς να μετράμε λογάριθμους, δηλ. ξεφορτωθείτε το σημάδι «κούτσουρο». Αρχικά, σημειώνουμε ότι δύο σημαντικά γεγονότα προκύπτουν από τον ορισμό:
- Το όρισμα και η βάση πρέπει πάντα να είναι μεγαλύτερα από το μηδέν. Αυτό προκύπτει από τον ορισμό του βαθμού από έναν ορθολογικό εκθέτη, στον οποίο ανάγεται ο ορισμός του λογάριθμου.
- Η βάση πρέπει να είναι διαφορετική από τη μονάδα, αφού μια μονάδα σε οποιαδήποτε δύναμη εξακολουθεί να είναι μια μονάδα. Εξαιτίας αυτού, το ερώτημα «σε ποια δύναμη πρέπει να υψωθεί κανείς για να πάρει δύο» είναι άνευ σημασίας. Δεν υπάρχει τέτοιο πτυχίο!
Τέτοιοι περιορισμοί ονομάζονται έγκυρο εύρος(ΟΔΖ). Αποδεικνύεται ότι το ODZ του λογαρίθμου μοιάζει με αυτό: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Σημειώστε ότι δεν υπάρχουν περιορισμοί στον αριθμό b (η τιμή του λογάριθμου) δεν επιβάλλεται. Για παράδειγμα, ο λογάριθμος μπορεί κάλλιστα να είναι αρνητικός: log 2 0,5 = −1, επειδή 0,5 = 2 −1 .
Ωστόσο, τώρα εξετάζουμε μόνο αριθμητικές εκφράσεις, όπου δεν απαιτείται να γνωρίζουμε το ODZ του λογαρίθμου. Όλοι οι περιορισμοί έχουν ήδη ληφθεί υπόψη από τους μεταγλωττιστές των προβλημάτων. Αλλά όταν μπαίνουν στο παιχνίδι οι λογαριθμικές εξισώσεις και οι ανισότητες, οι απαιτήσεις του DHS θα γίνουν υποχρεωτικές. Πράγματι, στη βάση και το επιχείρημα μπορεί να υπάρχουν πολύ ισχυρές κατασκευές, οι οποίες δεν ανταποκρίνονται απαραίτητα στους παραπάνω περιορισμούς.
Τώρα εξετάστε το γενικό σχήμα για τον υπολογισμό των λογαρίθμων. Αποτελείται από τρία βήματα:
- Να εκφράσετε τη βάση α και το όρισμα x ως δύναμη με τη μικρότερη δυνατή βάση μεγαλύτερη από το ένα. Στην πορεία, είναι καλύτερα να απαλλαγείτε από δεκαδικά κλάσματα.
- Λύστε την εξίσωση για τη μεταβλητή b: x = a b ;
- Ο αριθμός β που προκύπτει θα είναι η απάντηση.
Αυτό είναι όλο! Εάν ο λογάριθμος αποδειχθεί παράλογος, αυτό θα φανεί ήδη στο πρώτο βήμα. Η απαίτηση να είναι η βάση μεγαλύτερη από μία είναι πολύ σχετική: αυτό μειώνει την πιθανότητα λάθους και απλοποιεί σημαντικά τους υπολογισμούς. Ομοίως με τα δεκαδικά κλάσματα: αν τα μετατρέψετε αμέσως σε συνηθισμένα, θα υπάρχουν πολλαπλάσια λιγότερα σφάλματα.
Ας δούμε πώς λειτουργεί αυτό το σχήμα με συγκεκριμένα παραδείγματα:
Εργο. Υπολογίστε τον λογάριθμο: log 5 25
- Ας αναπαραστήσουμε τη βάση και το όρισμα ως δύναμη του πέντε: 5 = 5 1 ; 25 = 52;
- Ας φτιάξουμε και λύσουμε την εξίσωση:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2; - Λάβαμε απάντηση: 2.
Εργο. Υπολογίστε τον λογάριθμο:
[λεζάντα εικόνας]
Εργο. Υπολογίστε τον λογάριθμο: log 4 64
- Ας αναπαραστήσουμε τη βάση και το όρισμα ως δύναμη δύο: 4 = 2 2 ; 64 = 26;
- Ας φτιάξουμε και λύσουμε την εξίσωση:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3; - Έλαβε απάντηση: 3.
Εργο. Υπολογίστε τον λογάριθμο: log 16 1
- Ας αναπαραστήσουμε τη βάση και το όρισμα ως δύναμη δύο: 16 = 2 4 ; 1 = 20;
- Ας φτιάξουμε και λύσουμε την εξίσωση:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0; - Λήψη απάντησης: 0.
Εργο. Υπολογίστε τον λογάριθμο: log 7 14
- Ας αναπαραστήσουμε τη βάση και το όρισμα ως δύναμη του επτά: 7 = 7 1 ; Το 14 δεν αναπαρίσταται ως δύναμη του επτά, επειδή το 7 1< 14 < 7 2 ;
- Από την προηγούμενη παράγραφο προκύπτει ότι ο λογάριθμος δεν λαμβάνεται υπόψη.
- Η απάντηση είναι καμία αλλαγή: ημερολόγιο 7 14.
Μια μικρή σημείωση για το τελευταίο παράδειγμα. Πώς να βεβαιωθείτε ότι ένας αριθμός δεν είναι ακριβής δύναμη ενός άλλου αριθμού; Πολύ απλό - απλώς αποσυνθέστε το σε πρωταρχικούς παράγοντες. Και αν τέτοιοι παράγοντες δεν μπορούν να συγκεντρωθούν σε βαθμό με τους ίδιους δείκτες, τότε ο αρχικός αριθμός δεν είναι ακριβής βαθμός.
Εργο. Μάθετε αν οι ακριβείς δυνάμεις του αριθμού είναι: 8; 48; 81; 35; 14.
8 \u003d 2 2 2 \u003d 2 3 είναι ο ακριβής βαθμός, επειδή υπάρχει μόνο ένας πολλαπλασιαστής.
48 = 6 8 = 3 2 2 2 2 = 3 2 4 δεν είναι ακριβής ισχύς γιατί υπάρχουν δύο παράγοντες: 3 και 2.
81 \u003d 9 9 \u003d 3 3 3 3 \u003d 3 4 - ακριβής βαθμός.
35 \u003d 7 5 - και πάλι όχι ακριβής βαθμός.
14 \u003d 7 2 - και πάλι όχι ακριβής βαθμός.
Σημειώστε επίσης ότι οι ίδιοι οι πρώτοι αριθμοί είναι πάντα ακριβείς δυνάμεις του εαυτού τους.
Δεκαδικός λογάριθμος
Μερικοί λογάριθμοι είναι τόσο συνηθισμένοι που έχουν ειδική ονομασία και ονομασία.
Ο δεκαδικός λογάριθμος του ορίσματος x είναι ο λογάριθμος βάσης 10, δηλ. τη δύναμη στην οποία πρέπει να σηκώσετε τον αριθμό 10 για να πάρετε τον αριθμό x. Ονομασία: lg x .
Για παράδειγμα, log 10 = 1; log 100 = 2; lg 1000 = 3 - κ.λπ.
Από εδώ και στο εξής, όταν βλέπετε μια φράση όπως «Βρείτε το lg 0.01» σε ένα σχολικό βιβλίο, να ξέρετε ότι δεν πρόκειται για τυπογραφικό λάθος. Αυτός είναι ο δεκαδικός λογάριθμος. Ωστόσο, εάν δεν είστε συνηθισμένοι σε έναν τέτοιο χαρακτηρισμό, μπορείτε πάντα να τον ξαναγράψετε:
log x = log 10 x
Ό,τι ισχύει για τους συνηθισμένους λογάριθμους ισχύει και για τους δεκαδικούς.
φυσικός λογάριθμος
Υπάρχει ένας άλλος λογάριθμος που έχει τη δική του σημείωση. Κατά μία έννοια, είναι ακόμη πιο σημαντικό από το δεκαδικό. Αυτός είναι ο φυσικός λογάριθμος.
Ο φυσικός λογάριθμος του ορίσματος x είναι ο λογάριθμος στη βάση e , δηλ. η δύναμη στην οποία πρέπει να αυξηθεί ο αριθμός e για να ληφθεί ο αριθμός x. Ονομασία: ln x .
Πολλοί θα ρωτήσουν: ποιος άλλος είναι ο αριθμός e; Αυτός είναι ένας παράλογος αριθμός, η ακριβής τιμή του δεν μπορεί να βρεθεί και να γραφτεί. Εδώ είναι μόνο οι πρώτοι αριθμοί:
e = 2,718281828459...
Δεν θα εμβαθύνουμε στο τι είναι αυτός ο αριθμός και γιατί χρειάζεται. Απλώς θυμηθείτε ότι το e είναι η βάση του φυσικού λογάριθμου:
ln x = log e x
Έτσι ln e = 1; log e 2 = 2; ln e 16 = 16 - κ.λπ. Από την άλλη πλευρά, το ln 2 είναι ένας παράλογος αριθμός. Γενικά, ο φυσικός λογάριθμος οποιουδήποτε ρητού αριθμού είναι παράλογος. Εκτός φυσικά από την ενότητα: ln 1 = 0.
Για τους φυσικούς λογάριθμους, ισχύουν όλοι οι κανόνες που ισχύουν για τους συνηθισμένους λογάριθμους.
ΟΡΙΣΜΟΣ
Δεκαδικός λογάριθμοςονομάζεται λογάριθμος της βάσης 10:
Title="(!LANG:Απόδοση από QuickLaTeX.com">!}
Αυτός ο λογάριθμος είναι η λύση της εκθετικής εξίσωσης. Μερικές φορές (ειδικά στην ξένη βιβλιογραφία) ο δεκαδικός λογάριθμος συμβολίζεται επίσης ως, αν και οι δύο πρώτοι προσδιορισμοί είναι επίσης εγγενείς στον φυσικό λογάριθμο.
Οι πρώτοι πίνακες δεκαδικών λογαρίθμων δημοσιεύθηκαν από τον Άγγλο μαθηματικό Henry Briggs (1561-1630) το 1617 (γι' αυτό οι ξένοι επιστήμονες συχνά αποκαλούν τους δεκαδικούς λογάριθμους ακόμα Briggs), αλλά αυτοί οι πίνακες περιείχαν σφάλματα. Με βάση τους πίνακες (1783) του Σλοβένου και Αυστριακού μαθηματικού Georg Bartalomej Vega (Yuri Veha ή Vehovets, 1754-1802), το 1857 ο Γερμανός αστρονόμος και τοπογράφος Karl Bremiker (1804-1877) δημοσίευσε την πρώτη αλάνθαστη έκδοση. Με τη συμμετοχή του Ρώσου μαθηματικού και δασκάλου Leonty Filippovich Magnitsky (Telyatin ή Telyashin, 1669-1739), το 1703 δημοσιεύτηκαν στη Ρωσία οι πρώτοι πίνακες λογαρίθμων. Οι δεκαδικοί λογάριθμοι έχουν χρησιμοποιηθεί ευρέως για υπολογισμούς.
Ιδιότητες Δεκαδικών Λογαρίθμων
Αυτός ο λογάριθμος έχει όλες τις ιδιότητες ενός λογάριθμου σε μια αυθαίρετη βάση:
1. Βασική λογαριθμική ταυτότητα:
5. ![]() .
.
7. Μετάβαση σε νέα βάση:
![]()
Η συνάρτηση δεκαδικού λογάριθμου είναι συνάρτηση. Η γραφική παράσταση αυτής της καμπύλης αναφέρεται συχνά ως λογαριθμική.
Ιδιότητες συνάρτησης y=lg x
1) Τομέας ορισμού: .
2) Σύνολο τιμών: .
3) Γενική λειτουργία.
4) Η συνάρτηση είναι μη περιοδική.
5) Η γραφική παράσταση της συνάρτησης τέμνεται με τον άξονα x στο σημείο .
6) Κενά συνέπειας: title="(!LANG:Απόδοση από QuickLaTeX.com" height="16" width="44" style="vertical-align: -4px;"> для !} ![]() ότι για .
ότι για .
Συχνά πάρτε τον αριθμό δέκα. Οι λογάριθμοι των αριθμών στη βάση του δέκα καλούνται δεκαδικός. Κατά την εκτέλεση υπολογισμών με τον δεκαδικό λογάριθμο, είναι σύνηθες να λειτουργούμε με το πρόσημο lg, αλλά όχι κούτσουρο; ενώ δεν αναγράφεται ο αριθμός δέκα που καθορίζει τη βάση. Ναι, αντικαθιστούμε ημερολόγιο 10 105να απλοποιηθεί lg105; ένα log102στο lg2.
Για δεκαδικούς λογάριθμουςτυπικά είναι τα ίδια χαρακτηριστικά που έχουν οι λογάριθμοι με βάση μεγαλύτερη από μία. Δηλαδή, οι δεκαδικοί λογάριθμοι χαρακτηρίζονται αποκλειστικά για θετικούς αριθμούς. Οι δεκαδικοί λογάριθμοι αριθμών μεγαλύτεροι του ενός είναι θετικοί και οι αριθμοί μικρότεροι του ενός είναι αρνητικοί. από δύο μη αρνητικούς αριθμούς, ο μεγαλύτερος δεκαδικός λογάριθμος είναι ισοδύναμος με τον μεγαλύτερο, κ.λπ. Επιπλέον, οι δεκαδικοί λογάριθμοι έχουν διακριτικά χαρακτηριστικά και ιδιόμορφα χαρακτηριστικά, που εξηγούν γιατί είναι άνετο να προτιμάτε τον αριθμό δέκα ως βάση των λογαρίθμων.
Πριν αναλύσουμε αυτές τις ιδιότητες, ας ρίξουμε μια ματιά στις παρακάτω συνθέσεις.
Ακέραιο μέρος του δεκαδικού λογάριθμου ενός αριθμού έναπου ονομάζεται χαρακτηριστικό γνώρισμα, και το κλασματικό μάντισσααυτόν τον λογάριθμο.
Χαρακτηριστικό του δεκαδικού λογάριθμου ενός αριθμού έναυποδεικνύεται ως , και η μάντισσα ως (lg ένα}.
Ας πάρουμε, ας πούμε, lg 2 ≈ 0,3010. Κατά συνέπεια, = 0, (log 2) ≈ 0,3010.
Το ίδιο ισχύει για το lg 543.1 ≈2.7349. Συνεπώς, = 2, (lg 543,1)≈ 0,7349.
Ο υπολογισμός των δεκαδικών λογαρίθμων των θετικών αριθμών από πίνακες χρησιμοποιείται αρκετά ευρέως.
Χαρακτηριστικά σημάδια δεκαδικών λογαρίθμων.
Το πρώτο πρόσημο του δεκαδικού λογάριθμου.ένας μη αρνητικός ακέραιος που αντιπροσωπεύεται από το 1 ακολουθούμενο από μηδενικά είναι ένας θετικός ακέραιος αριθμός ίσος με τον αριθμό των μηδενικών στον επιλεγμένο αριθμό .
Ας πάρουμε lg 100 = 2, lg 1 00000 = 5.
Σε γενικές γραμμές, αν
Οτι ένα= 10n , από το οποίο παίρνουμε
lg a = lg 10 n = n lg 10 =Π.
Δεύτερο σημάδι.Ο δεκαδικός λογάριθμος ενός θετικού δεκαδικού, που φαίνεται από ένα με μηδενικά, είναι − Π, που Π- τον αριθμό των μηδενικών στην αναπαράσταση αυτού του αριθμού, λαμβάνοντας υπόψη το μηδέν των ακεραίων.
Σκεφτείτε , lg 0,001 = -3, lg 0,000001 = -6.
Σε γενικές γραμμές, αν
,
Οτι ένα= 10-n και αποδεικνύεται
lga = lg 10n =-n lg 10 =-n
Τρίτο σημάδι.Το χαρακτηριστικό του δεκαδικού λογάριθμου ενός μη αρνητικού αριθμού μεγαλύτερου του ενός είναι ίσο με τον αριθμό των ψηφίων στο ακέραιο μέρος αυτού του αριθμού, εξαιρουμένου του ενός.
Ας αναλύσουμε αυτό το χαρακτηριστικό 1) Το χαρακτηριστικό του λογαρίθμου lg 75.631 ισοδυναμεί με 1.
Πράγματι, 10< 75,631 < 100. Из этого можно сделать вывод
lg 10< lg 75,631 < lg 100,
1 < lg 75,631 < 2.
Αυτό υπονοεί,
lg 75.631 = 1 + b,
Η μετατόπιση ενός κόμματος σε ένα δεκαδικό κλάσμα προς τα δεξιά ή προς τα αριστερά ισοδυναμεί με τη λειτουργία πολλαπλασιασμού αυτού του κλάσματος με δύναμη του δέκα με ακέραιο εκθέτη Π(θετικό ή αρνητικό). Και επομένως, όταν η υποδιαστολή σε ένα θετικό δεκαδικό κλάσμα μετατοπίζεται προς τα αριστερά ή προς τα δεξιά, η μάντισσα του δεκαδικού λογάριθμου αυτού του κλάσματος δεν αλλάζει.
Άρα, (log 0,0053) = (log 0,53) = (log 0,0000053).