Progetto di algebra "Soluzione di disuguaglianze trigonometriche" Completato da una studentessa della classe 10 "B" Julia Kazachkova Supervisore: insegnante di matematica Kochakova N.N.
Scopo Consolidare il materiale sull'argomento "Risoluzione delle disuguaglianze trigonometriche" e creare un promemoria per gli studenti per prepararsi al prossimo esame.
Obiettivi Riassumi il materiale sull'argomento. Organizza le informazioni ricevute. Prendere in considerazione questo argomento nell'esame.
Rilevanza La rilevanza dell'argomento che ho scelto sta nel fatto che i compiti sull'argomento "Soluzione di disuguaglianze trigonometriche" sono inclusi nei compiti dell'esame.
Disuguaglianze trigonometriche Una disuguaglianza è una relazione che collega due numeri o espressioni attraverso uno dei segni: (maggiore di); ≥ (maggiore o uguale a). Una disuguaglianza trigonometrica è una disuguaglianza contenente funzioni trigonometriche.
Disuguaglianze trigonometriche La soluzione delle disuguaglianze contenenti funzioni trigonometriche si riduce, di regola, alla soluzione delle disuguaglianze più semplici della forma: sin x>a, sin x a, cosx a,tx a, ctg x
Algoritmo per risolvere le disuguaglianze trigonometriche Sull'asse corrispondente a una data funzione trigonometrica, segnare il dato valore numerico di questa funzione. Disegna una linea attraverso il punto contrassegnato che interseca il cerchio unitario. Seleziona i punti di intersezione della retta e del cerchio, tenendo conto del segno di disuguaglianza stretta o non stretta. Seleziona l'arco del cerchio su cui si trovano le soluzioni della disuguaglianza. Determina i valori degli angoli nei punti iniziale e finale dell'arco circolare. Annotare la soluzione della disuguaglianza, tenendo conto della periodicità della data funzione trigonometrica.
Formule per risolvere le disuguaglianze trigonometriche sinx >a; x (arcoseno a + 2πn; π- arcoseno a + 2πn). sinx UN; x (- arccos a + 2πn; arccos a + 2πn). cosxUN; x (arctg a + πn ; + πn). tgx UN; x (πn ; arctg + πn). ctgx
Soluzione grafica disuguaglianze trigonometriche di base sinx >a
Soluzione grafica delle principali disuguaglianze trigonometriche sinx Soluzione grafica delle principali disuguaglianze trigonometriche cosx >a Soluzione grafica delle principali disuguaglianze trigonometriche cosx Soluzione grafica delle principali disuguaglianze trigonometriche tgx >a Soluzione grafica delle principali disuguaglianze trigonometriche tgx Soluzione grafica delle principali disuguaglianze trigonometriche ctgx >a
Le disuguaglianze sono relazioni della forma a › b, dove a e b sono espressioni contenenti almeno una variabile. Le disuguaglianze possono essere strette - ‹, › e non strette - ≥, ≤.
Le disuguaglianze trigonometriche sono espressioni della forma: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, in cui F(x) è rappresentata da una o più funzioni trigonometriche .
Un esempio della più semplice disuguaglianza trigonometrica è: sin x ‹ 1/2. È consuetudine risolvere graficamente tali problemi, per questo sono stati sviluppati due metodi.
Metodo 1 - Risolvere le disuguaglianze tracciando una funzione
Per trovare un intervallo che soddisfi le condizioni della disuguaglianza sin x ‹ 1/2, devi fare quanto segue:
- Sull'asse delle coordinate, costruisci una sinusoide y = sin x.
- Disegna un grafico sullo stesso asse argomento numerico disuguaglianza, cioè una retta passante per il punto ½ dell'ordinata.
- Segna i punti di intersezione dei due grafici.
- Ombreggia il segmento che è la soluzione dell'esempio.
Quando ci sono segni forti in un'espressione, i punti di intersezione non sono soluzioni. Poiché il più piccolo periodo positivo della sinusoide è 2π, scriviamo la risposta come segue:
![]()
Se i segni dell'espressione non sono rigorosi, l'intervallo di soluzione deve essere racchiuso tra parentesi quadre - . La risposta al problema può anche essere scritta come un'altra disuguaglianza: ![]()
Metodo 2 - Risoluzione delle disuguaglianze trigonometriche utilizzando la circonferenza unitaria
Problemi simili possono essere facilmente risolti con l'aiuto di un cerchio trigonometrico. L'algoritmo di ricerca è molto semplice:
- Innanzitutto, disegna un cerchio unitario.
- Quindi devi annotare il valore della funzione dell'arco dell'argomento del lato destro della disuguaglianza sull'arco del cerchio.
- È necessario tracciare una retta passante per il valore della funzione arco parallela all'asse x (OX).
- Dopodiché, resta solo da selezionare l'arco di cerchio, che è l'insieme delle soluzioni della disuguaglianza trigonometrica.
- Scrivi la risposta nel modulo richiesto.
Analizziamo i passaggi della soluzione usando la disuguaglianza sin x › 1/2 come esempio. I punti α e β sono contrassegnati sul cerchio: i valori
![]()
I punti dell'arco situati sopra α e β sono l'intervallo per risolvere la data disuguaglianza.

Se devi risolvere un esempio per cos, l'arco delle risposte sarà posizionato simmetricamente rispetto all'asse OX e non OY. Puoi considerare la differenza tra gli intervalli di soluzione per sin e cos nei diagrammi sottostanti nel testo.

Le soluzioni grafiche per le disuguaglianze tangenti e cotangenti differiranno sia da seno che da coseno. Ciò è dovuto alle proprietà delle funzioni.

L'arcotangente e l'arcotangente sono tangenti al cerchio trigonometrico e il periodo positivo minimo per entrambe le funzioni è π. Per utilizzare rapidamente e correttamente il secondo metodo, è necessario ricordare su quale asse vengono tracciati i valori di sin, cos, tg e ctg.
La tangente tangente corre parallela all'asse OY. Se tracciamo il valore di arctg a sulla circonferenza unitaria, il secondo punto richiesto si troverà nel quarto diagonale. angoli
Sono punti di interruzione per la funzione, poiché il grafico tende a raggiungerli ma non li raggiunge mai.

Nel caso della cotangente, la tangente corre parallela all'asse OX e la funzione si interrompe nei punti π e 2π.

Disuguaglianze trigonometriche complesse
Se l'argomento della funzione di disuguaglianza è rappresentato non solo da una variabile, ma da un'intera espressione contenente un'incognita, allora stiamo già parlando di disuguaglianza complessa. Il corso e l'ordine della sua soluzione sono in qualche modo diversi dai metodi sopra descritti. Supponiamo di dover trovare una soluzione alla seguente disuguaglianza:

La soluzione grafica prevede la costruzione di una sinusoide ordinaria y = sin x per valori di x scelti arbitrariamente. Calcoliamo una tabella con le coordinate per i punti di riferimento del grafico:

Il risultato dovrebbe essere una bella curva.
Per facilitare la ricerca di una soluzione, sostituiamo l'argomento della funzione complessa

L'intersezione di due grafici consente di determinare l'area dei valori desiderati per i quali è soddisfatta la condizione di disuguaglianza.

Il segmento trovato è la soluzione per la variabile t:

Tuttavia, l'obiettivo dell'attività è trovare tutto opzioni possibili sconosciuto x:

Risolvere la doppia disuguaglianza è abbastanza semplice, devi spostare π / 3 nelle parti estreme dell'equazione ed eseguire i calcoli richiesti:

Risposta al compito sembrerà un intervallo per la disuguaglianza stretta:

Tali compiti richiederanno l'esperienza e l'abilità degli studenti nella gestione delle funzioni trigonometriche. Più compiti di formazione sarà deciso nel processo di preparazione, più facile e veloce lo studente troverà la risposta UTILIZZARE la domanda test.
DEFINIZIONE
Le disuguaglianze trigonometriche sono disuguaglianze che contengono una variabile sotto il segno di una funzione trigonometrica.
Risoluzione di disuguaglianze trigonometriche
La soluzione delle disuguaglianze trigonometriche spesso si riduce alla risoluzione delle disuguaglianze trigonometriche più semplici della forma: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname(tg) x > a \ ), \(\ \ operatorname(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \operatorname(tg) x \ leq a \), \ (\ \operatorname(ctg) x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \operatorname(tg ) x \geq a \ ), \(\ \operatorname(tg) x \geq a \)
Le disuguaglianze trigonometriche più semplici vengono risolte graficamente o utilizzando un cerchio trigonometrico unitario.
Per definizione, il seno dell'angolo \(\ \alpha \) è l'ordinata del punto \(\ P_(\alpha)(x, y) \) della circonferenza unitaria (Fig. 1), e il coseno è l'ascissa di questo punto. Questo fatto viene utilizzato per risolvere le più semplici disuguaglianze trigonometriche con coseno e seno utilizzando il cerchio unitario.
Esempi di risoluzione di disuguaglianze trigonometriche
Risolvi la disuguaglianza \(\ \sin x \leq \frac(\sqrt(3))(2) \)
Poiché \(\ \left|\frac(\sqrt(3))(2)\right| , questa disuguaglianza ha una soluzione e può essere risolta in due modi
Primo modo. Risolviamo graficamente questa disuguaglianza. Per fare questo, costruiamo nello stesso sistema di coordinate un grafico del seno \(\ y=\sin x \) (Fig. 2) e la retta \(\ y=\frac(\sqrt(3))( 2) \)
Selezioniamo gli intervalli in cui si trova la sinusoide sotto il grafico della retta \(\ y=\frac(\sqrt(3))(2) \) . Trova le ascisse \(\ x_(1) \) e \(\ x_(2) \) dei punti di intersezione di questi grafici: \(\ x_(1)=\pi-\arcsin \frac(\sqrt(3 ))(2 )=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Abbiamo ottenuto l'intervallo \(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \) ma poiché la funzione \(\ y=\sin x \) è periodica e ha un periodo \(\ 2 \pi \) , allora la risposta è l'unione di intervalli: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+ 2 \pi k\destra] \), \(\ k \in Z \)
Il secondo modo. Costruisci una circonferenza unitaria e una retta \(\ y=\frac(\sqrt(3))(2) \) , denota i loro punti di intersezione \(\ P_(x_(1)) \) e \(\ P_(x_ (2 )) \) (figura 3). La soluzione alla disuguaglianza originale sarà l'insieme dei punti ordinati che sono minori di \(\ \frac(\sqrt(3))(2) \) . Troviamo il valore di \(\ \boldsymbol(I)_(1) \) e \(\ \boldsymbol(I)_(2) \) andando in senso antiorario, \(\ x_(1) Fig. 3
\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Tenendo conto della periodicità della funzione seno, si ottengono infine gli intervalli \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \ pi\destra] \), \(\k\in Z\)
Risolvi la disuguaglianza \(\ \sin x>2 \)
Il seno è una funzione limitata: \(\ |\sin x| \leq 1 \) , e il lato destro di questa disuguaglianza è maggiore di uno, quindi non ci sono soluzioni.
Risolvi la disequazione \(\ \cos x>\frac(1)(2) \)
Questa disuguaglianza può essere risolta in due modi: graficamente e usando una circonferenza unitaria. Consideriamo ciascuno dei metodi.
Primo modo. Descriviamo in un sistema di coordinate le funzioni che descrivono le parti sinistra e destra della disuguaglianza, ovvero \(\ y=\cos x \) e \(\ y=\frac(1)(2) \) . Selezioniamo gli intervalli in cui il grafico della funzione coseno \(\ y=\cos x \) si trova sopra il grafico della retta \(\ y=\frac(1)(2) \) (Fig. 4 ).
Trova le ascisse dei punti \(\ \boldsymbol(x)_(1) \) e \(\ x_(2) \) - i punti di intersezione dei grafici delle funzioni \(\ y=\cos x \ ) e \(\ y=\frac (1)(2) \) , che sono gli estremi di uno degli intervalli su cui vale la disuguaglianza indicata. \(\ x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3) \); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)
Considerando che il coseno è una funzione periodica, con un periodo \(\ 2 \pi \) , la risposta è il valore \(\ x \) dagli intervalli \(\ \left(-\frac(\pi)(3 )+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k \in Z \)
Il secondo modo. Costruiamo la circonferenza unitaria e la retta \(\ x=\frac(1)(2) \) (poiché cerchio unitario i coseni corrispondono all'asse x). Siano \(\ P_(x_(1)) \) e \(\ P_(x_(2)) \) (Fig. 5) i punti di intersezione della linea e del cerchio unitario. La soluzione all'equazione originale sarà l'insieme dei punti di ascissa che sono minori di \(\ \frac(1)(2) \) . Trovare il valore di \(\ x_(1) \) e \(\ 2 \) , facendo un giro in senso antiorario in modo che \(\ x_(1) Tenendo conto della periodicità del coseno, si ottengono infine gli intervalli \( \ \left(-\frac (\pi)(3)+2 \pi k ;\frac(\pi)(3)+2 \pi k\right) \),\(\ k \in Z \)
Risolvi la disequazione \(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \)
Tracciamo i grafici delle funzioni \(\ y=\operatorname(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \) in un sistema di coordinate
Selezioniamo gli intervalli in cui il grafico della funzione \(\ y=\operatorname(ctg) x \) non è superiore al grafico della retta \(\ y=-\frac(\sqrt(3))(3 ) \) (figura 6) .
Trova l'ascissa del punto \(\ x_(0) \) , che è la fine di uno degli intervalli su cui la disuguaglianza \(\ x_(0)=\operatorname(arcctg)\left(-\frac(\ sqrt(3))( 3)\right)=\pi-\operatorname(arcctg)\left(\frac(\sqrt(3))(3)\right)=\pi-\frac(\pi)(3 )=\frac(2 \pi)(3) \)
L'altra estremità di questo gap è il punto \(\ \pi \) , e la funzione \(\ y=\operatorname(ctg) x \) non è definita a questo punto. Quindi, una delle soluzioni a questa disuguaglianza è l'intervallo \(\ \frac(2 \pi)(3) \leq x
Disuguaglianze trigonometriche con argomento complesso
Le disuguaglianze trigonometriche con un argomento complesso possono essere ridotte alle più semplici disuguaglianze trigonometriche usando una sostituzione. Dopo averlo risolto, viene effettuata la sostituzione inversa e viene espressa l'incognita originale.
Risolvi la disequazione \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)
Esprimi il coseno a destra di questa disuguaglianza: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)
Eseguiamo la sostituzione \(\ t=2 x+100^(\circ) \) , dopodiché questa disuguaglianza viene trasformata nella più semplice disuguaglianza \(\ \cos t \leq-\frac(1)(2) \ )
Risolviamolo usando la circonferenza unitaria. Costruiamo un cerchio unitario e una linea \(\ x=-\frac(1)(2) \) . Indichiamo \(\ P_(1) \) e \(\ P_(2) \) come i punti di intersezione della linea e del cerchio unitario (Fig. 7).
La soluzione alla disuguaglianza originale sarà l'insieme dei punti di ascissa, che sono al massimo \(\ -\frac(1)(2) \). Il punto \(\ P_(1) \) corrisponde all'angolo \(\ 120^(\circ) \) , e il punto \(\ P_(2) \) . Quindi, dato il periodo del coseno, otteniamo \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \ ) , \(\ n \in Z \)
Facciamo la sostituzione inversa \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ (\ circ)+360^(\circ) \cdot n \), \(\ n \in Z \)
Esprimiamo \(\ \mathbf(x) \), per fare ciò, prima sottraiamo \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot n \leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \ n\in Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z\)
e poi, dividi per 2 \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^ (\circ)+360^(\circ) \cdot n)(2) \), \(\ n \in Z \); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \in Z \)
Disuguaglianze trigonometriche doppie
Risolvi la doppia disuguaglianza trigonometrica \(\ \frac(1)(2)
Introduciamo la sostituzione \(\ t=\frac(x)(2) \) , quindi la disuguaglianza originale assumerà la forma \(\ \frac(1)(2)
Risolviamolo usando la circonferenza unitaria. Poiché l'asse delle ordinate corrisponde al seno sulla circonferenza unitaria, selezioniamo su di esso l'insieme delle ordinate di cui è maggiore di \(\ x=\frac(1)(2) \) e minore o uguale a \(\ \frac(\sqrt(2))(2 ) \) . Nella Figura 8, questi punti saranno posizionati sugli archi \(\ P_(t_(1)) \), \(\ P_(t_(2)) \) e \(\ P_(t_(3)) \) , \( \ P_(t_(4)) \) . Troviamo il valore \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) , facendo un giro in senso antiorario, e \ (\ t_(1) \(\ t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3 \ pi)(4) \); \(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi ) (6)\)
Otteniamo così due intervalli che, tenendo conto della periodicità della funzione seno, possono essere scritti come segue \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \) , \(\ \frac(3 \pi)(4)+2 \pi k Express \(\ \mathbf( x) \), per questo moltiplichiamo tutti i lati di entrambe le disuguaglianze per 2, otteniamo \(\ \frac (\pi)(3)+4 \pik \leq x
Nella lezione pratica ripeteremo i principali tipi di compiti dall'argomento "Trigonometria", analizzeremo inoltre problemi di maggiore complessità e prenderemo in considerazione esempi di risoluzione di varie disuguaglianze trigonometriche e dei loro sistemi.
Questa lezione ti aiuterà a prepararti per uno dei tipi di compiti B5, B7, C1 e C3.
Iniziamo ripetendo i principali tipi di compiti che abbiamo esaminato nell'argomento Trigonometria e risolviamo diversi compiti non standard.
Compito n. 1. Converti gli angoli in radianti e gradi: a) ; B) .
a) Usa la formula per convertire i gradi in radianti
![]()
Sostituisci il valore dato in esso.
b) Applicare la formula per convertire i radianti in gradi
![]()
Eseguiamo la sostituzione ![]() .
.
Risposta. UN) ; B) .
Compito n. 2. Calcola: a) ; B) .
a) Poiché l'angolo è molto oltre la tabella, lo riduciamo sottraendo il periodo del seno. Perché l'angolo è espresso in radianti, quindi il periodo sarà considerato come .
b) In questo caso, la situazione è simile. Poiché l'angolo è specificato in gradi, considereremo il periodo della tangente come .
L'angolo risultante, sebbene inferiore al periodo, è maggiore, il che significa che non si riferisce più alla parte principale, ma alla parte estesa del tavolo. Per non allenare ancora una volta la nostra memoria memorizzando una tabella estesa di valori di trigofunzioni, sottraiamo nuovamente il periodo tangente:
Abbiamo approfittato della stranezza della funzione tangente.
Risposta. a) 1; B) .
Compito n. 3. Calcolare ![]() , Se .
, Se .
Portiamo l'intera espressione alle tangenti dividendo il numeratore e il denominatore della frazione per . Allo stesso tempo, non possiamo averne paura, perché in questo caso il valore della tangente non esisterebbe.
Compito n. 4. Semplifica l'espressione.
Le espressioni specificate vengono convertite utilizzando formule cast. È solo che sono insolitamente scritti usando gradi. La prima espressione è generalmente un numero. Semplifica tutte le trigofunzioni a turno:
Perché , allora la funzione diventa una cofunzione, cioè alla cotangente, e l'angolo cade nel secondo quarto, in cui il segno della tangente originaria è negativo.

Per gli stessi motivi dell'espressione precedente, la funzione cambia in una cofunzione, cioè alla cotangente, e l'angolo cade nel primo quarto, in cui la tangente iniziale ha segno positivo.
Sostituendo tutto in un'espressione semplificata:
Compito n. 5. Semplifica l'espressione.
Scriviamo la tangente del doppio angolo secondo la formula corrispondente e semplifichiamo l'espressione:
L'ultima identità è una delle formule di sostituzione universali per il coseno.
Compito n. 6. Calcola.
La cosa principale è non fare un errore standard e non dare una risposta che l'espressione è uguale a . È impossibile utilizzare la proprietà principale dell'arcotangente mentre c'è un fattore sotto forma di due vicino ad essa. Per sbarazzarcene, scriviamo l'espressione secondo la formula per la tangente di un doppio angolo, mentre la trattiamo come un argomento ordinario.
![]()
Ora è già possibile applicare la proprietà principale dell'arcotangente, ricorda che non ci sono restrizioni sul suo risultato numerico.
Compito n. 7. Risolvi l'equazione.
Al momento di decidere equazione frazionaria, che è uguale a zero, è sempre indicato che il numeratore è zero e il denominatore no, perché non puoi dividere per zero.

La prima equazione è caso speciale l'equazione più semplice, che viene risolta usando un cerchio trigonometrico. Pensa tu stesso a questa soluzione. La seconda disuguaglianza è risolta come l'equazione più semplice usando la formula generale per le radici della tangente, ma solo con il segno diverso.

Come possiamo vedere, una famiglia di radici esclude un'altra esattamente la stessa famiglia di radici che non soddisfano l'equazione. Quelli. non ci sono radici.
Risposta. Non ci sono radici.
Compito n. 8. Risolvi l'equazione.
Nota subito che puoi eliminare il fattore comune e farlo:
L'equazione è stata ridotta a una delle forme standard, quando il prodotto di più fattori è uguale a zero. Sappiamo già che in questo caso uno di essi è uguale a zero, o l'altro o il terzo. Scriviamo questo come un insieme di equazioni:

Le prime due equazioni sono casi speciali delle più semplici, abbiamo già incontrato molte volte equazioni simili, quindi indicheremo immediatamente le loro soluzioni. Riduciamo la terza equazione a una funzione usando la formula del seno a doppio angolo.

Risolviamo l'ultima equazione separatamente:
![]()
Questa equazione non ha radici, perché il valore del seno non può andare oltre ![]() .
.
Pertanto, solo le prime due famiglie di radici sono la soluzione, possono essere combinate in una, che è facile da mostrare su un cerchio trigonometrico:
 |
Questa è una famiglia di tutte le metà, ad es.
Passiamo alla risoluzione delle disuguaglianze trigonometriche. Innanzitutto, analizziamo l'approccio alla risoluzione di un esempio senza utilizzare formule di soluzione generali, ma con l'aiuto di un cerchio trigonometrico.
Compito n. 9. Risolvi la disuguaglianza.
Disegna una linea ausiliaria sul cerchio trigonometrico corrispondente al valore del seno uguale a , e mostra l'intervallo di angoli che soddisfano la disuguaglianza.
 |
È molto importante capire esattamente come specificare l'intervallo angolare risultante, ad es. qual è il suo inizio e qual è la sua fine. L'inizio del divario sarà l'angolo corrispondente al punto in cui entreremo proprio all'inizio del divario se ci spostiamo in senso antiorario. Nel nostro caso, questo è il punto che si trova a sinistra, perché muovendosi in senso antiorario e superando il punto giusto, invece, si esce dall'intervallo angolare richiesto. Il punto giusto corrisponderà quindi alla fine del gap.
Ora dobbiamo capire i valori degli angoli iniziale e finale del nostro gap di soluzioni alla disuguaglianza. Errore comuneè indicare subito che il punto destro corrisponde all'angolo , il sinistro e dare la risposta. Questo non è vero! Si noti che abbiamo appena indicato l'intervallo corrispondente alla parte superiore del cerchio, anche se a noi interessa quello inferiore, in altre parole, abbiamo confuso l'inizio e la fine dell'intervallo di soluzioni di cui abbiamo bisogno.
Affinché l'intervallo inizi all'angolo del punto destro e termini all'angolo del punto sinistro, il primo angolo specificato deve essere minore del secondo. Per fare questo, dovremo misurare l'angolo del punto giusto nella direzione di riferimento negativa, cioè in senso orario e sarà uguale a . Quindi, partendo da esso in senso orario positivo, arriveremo al punto destro dopo il punto sinistro e otterremo il valore dell'angolo per esso. Ora l'inizio dell'intervallo degli angoli è minore della fine di , e possiamo scrivere l'intervallo delle soluzioni senza tener conto del periodo:
Considerando che tali intervalli si ripeteranno un numero infinito di volte dopo qualsiasi numero intero di rotazioni, otteniamo la soluzione generale, tenendo conto del periodo sinusoidale:
Mettiamo parentesi tonde perché la disuguaglianza è stretta, e foriamo i punti del cerchio che corrispondono alle estremità dell'intervallo.
Confronta la tua risposta con la formula per la soluzione generale che abbiamo dato nella lezione.
Risposta. ![]() .
.
Questo metodo è utile per capire da dove provengono le formule per le soluzioni generali delle disuguaglianze trigonali più semplici. Inoltre, è utile per chi è troppo pigro per imparare tutte queste formule ingombranti. Tuttavia, anche il metodo in sé non è facile, scegli quale approccio alla soluzione è più conveniente per te.
Per risolvere le disuguaglianze trigonometriche si possono utilizzare anche i grafici delle funzioni su cui è costruita la retta ausiliaria, analogamente al metodo mostrato utilizzando la circonferenza unitaria. Se sei interessato, prova a capire tu stesso questo approccio alla soluzione. In quanto segue, useremo formule generali per risolvere le disuguaglianze trigonometriche più semplici.
Compito n. 10. Risolvi la disuguaglianza.
Usiamo la formula di soluzione generale, tenendo conto che la disuguaglianza non è stretta:
Otteniamo nel nostro caso:
Risposta. ![]()
Compito n. 11. Risolvi la disuguaglianza.
Usiamo la formula di soluzione generale per la corrispondente disuguaglianza stretta:
Risposta. ![]() .
.
Compito n. 12. Risolvere le disuguaglianze: a) ; B) .
In queste disuguaglianze, non bisogna affrettarsi a usare formule per soluzioni generali o cerchio trigonometrico, ricorda solo l'intervallo di seno e coseno.
a) Perché ![]() , allora la disuguaglianza non ha senso. Pertanto, non ci sono soluzioni.
, allora la disuguaglianza non ha senso. Pertanto, non ci sono soluzioni.
b) Perché analogamente, il seno di qualsiasi argomento soddisfa sempre la disuguaglianza specificata nella condizione. Pertanto, la disuguaglianza è soddisfatta da tutti i valori reali dell'argomento.
Risposta. a) non ci sono soluzioni; B) .
Compito 13. Risolvi la disuguaglianza ![]() .
.
Soluzione delle più semplici equazioni trigonometriche
Innanzitutto, ricordiamo le formule per risolvere le equazioni trigonometriche più semplici.
- $sinx=a$
- $cosx=a$
- $tgx=a$
- $ctgx=a$
Soluzione delle disuguaglianze trigonometriche più semplici.
Per risolvere le disuguaglianze trigonometriche più semplici, dobbiamo prima risolvere l'equazione corrispondente e quindi, utilizzando il cerchio trigonometrico, trovare una soluzione alla disuguaglianza. Considera le soluzioni delle disuguaglianze trigonometriche più semplici con esempi.
Esempio 1
$sinx\ge \frac(1)(2)$
Trova una soluzione alla disequazione trigonometrica $sinx=\frac(1)(2)$
\ \
Figura 1. Soluzione della disequazione $sinx\ge \frac(1)(2)$.
Poiché la disuguaglianza ha segno “maggiore o uguale”, la soluzione giace sull'arco superiore del cerchio (rispetto alla soluzione dell'equazione).
Risposta: $\left[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\right]$.
Esempio 2
Trova una soluzione alla disequazione trigonometrica $cosx=\frac(\sqrt(3))(2)$
\ \
Nota la soluzione sul cerchio trigonometrico
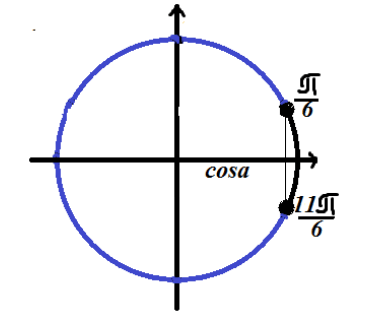
Poiché la disuguaglianza ha un segno “minore di”, la soluzione giace sull'arco di cerchio situato a sinistra (rispetto alla soluzione dell'equazione).
Risposta: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$.
Esempio 3
$tgx\le \frac(\sqrt(3))(3)$
Trova una soluzione alla disequazione trigonometrica $tgx=\frac(\sqrt(3))(3)$
\ \
Qui abbiamo anche bisogno di un dominio di definizione. Come ricordiamo, la funzione tangente $x\ne \frac(\pi )(2)+\pi n,n\in Z$
Nota la soluzione sul cerchio trigonometrico
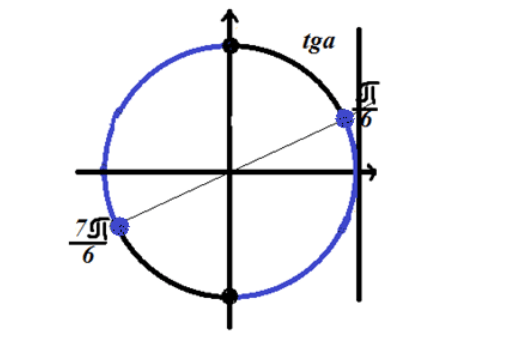
Figura 3. Soluzione della disequazione $tgx\le \frac(\sqrt(3))(3)$.
Poiché la disuguaglianza ha un segno "minore o uguale a", la soluzione si trova sugli archi del cerchio contrassegnati in blu nella figura 3.
Risposta: $\ \left(-\frac(\pi )(2)+2\pi n\right.,\left.\frac(\pi )(6)+2\pi n\right]\cup \left (\frac(\pi )(2)+2\pi n,\destra.\sinistra.\frac(7\pi )(6)+2\pi n\destra]$
Esempio 4
Trova una soluzione alla disuguaglianza trigonometrica $ctgx=\sqrt(3)$
\ \
Qui abbiamo anche bisogno di un dominio di definizione. Come ricordiamo, la funzione tangente $x\ne \pi n,n\in Z$
Nota la soluzione sul cerchio trigonometrico

Figura 4. Soluzione della disuguaglianza $ctgx\le \sqrt(3)$.
Poiché la disuguaglianza ha un segno "maggiore di", la soluzione si trova sugli archi del cerchio contrassegnati in blu nella Figura 4.
Risposta: $\ \left(2\pi n,\frac(\pi )(6)+2\pi n\right)\cup \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\destra)$