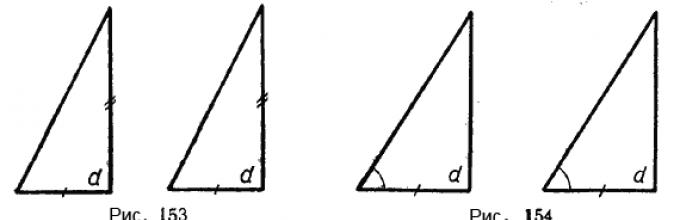
1. Prva dva znaka jednakosti pravokutnih trokuta.
Da bi dva trokuta bila jednaka, dovoljno je da su tri elementa jednog trokuta jednaka odgovarajućim elementima drugog trokuta, a najmanje jedna stranica sigurno mora biti uključena u broj tih elemenata.
Budući da su svi pravi kutovi jednaki jedni drugima, pravokutni trokuti već imaju jedan jednak element, točno jedan pravi kut.

Slijedi da su pravokutni trokuti jednaki:
ako su katete jednog trokuta jednake katetama drugog trokuta (slika 153);
ako su krak i susjedni oštri kut jednog trokuta jednaki katetu i susjedni oštri kut drugog trokuta (slika 154).
Dokažimo sada dva teorema koji uspostavljaju još dva kriterija za jednakost pravokutnih trokuta.
Teoremi o kriterijima za jednakost pravokutnih trokuta
Teorem 1. Ako su hipotenuza i akutni kut jednog trokuta jednaki hipotenuzi i akutni kut drugog trokuta, tada su takvi pravokutni trokuti jednaki.Da bismo dokazali ovaj teorem, konstruiramo dvije pravokutne katete ABC i A'B'C ', u kojima su kutovi A i A' jednaki, hipotenuze AB i A'B 'također su jednake, a kutovi C i C' jednaki ravne crte (slika 157) ...

Trokut ABC namećemo trokutu ABC tako da se vrh A 'podudara s vrhom A, hipotenuza AB' - s jednakom hipotenuzom AB. Tada će, zbog jednakosti kutova A i A ', krak A'C' slijediti krak AC; krak V'S 'bit će poravnat s krakom VS: obojica su okomice povučene na jednu ravnu crtu AC iz jedne točke B. Dakle, vrhovi C i C' podudarat će se.
Trokut ABC poravnan je s trokutom ABC.
Prema tome, \\ (\\ Delta \\) ABC \u003d \\ (\\ Delta \\) A'B'C '.
Ovaj teorem daje 3. test za jednakost pravokutnih trokuta (hipotenuzom i oštrim kutom).
Teorem 2. Ako su hipotenuza i kateta jednog trokuta jednaki hipotenuzi i katetu drugog trokuta, tada su takvi pravokutni trokuti jednaki.
Da bismo to dokazali, konstruiramo dva pravokutna trokut ABC i A'B'C ', u kojima su kutovi C i C' ravni, krakovi AC i A'C 'jednaki, hipotenuze AB i A'B' također su jednake (slika 158).

Nacrtajmo pravac MN i na njemu označimo točku C, od ove točke crtamo okomiti CK na pravac MN. Zatim pravokut trokuta ABC superpostavljamo na pravi kut CMM-a tako da se njihovi vrhovi podudaraju i krak AC-a ide uz zraku SC-a, zatim krak BC-a slijedi zrak CM-a. Stavite pravi kut trokuta A'B'C 'na pravi kut KCN tako da se njihovi vrhovi podudaraju i krak A'C' ide duž zrake CK, tada će krak C'B 'ići uz zraku CN. Vrhovi A i A 'podudarat će se zbog jednakosti krakova AC i A'C'.
Trokuti ABC i A'B'C 'bit će zajedno jednakokračan trokut BAB ', u kojem će AC biti visina i simetrala, a time i os simetrije trokuta BAB'. Iz ovoga slijedi da je \\ (\\ Delta \\) ABC \u003d \\ (\\ Delta \\) A'B'S '.
Ovaj teorem daje 4. test za jednakost pravokutnih trokuta (duž hipotenuze i katete).
Dakle, svi znakovi jednakosti pravokutnih trokuta:
1. Ako su dvije katete jednog pravokutnog trokuta jednake dvije katete drugog pravokutnog trokuta, tada su takvi pravokutni trokuti jednaki2. Ako su krak i susjedni oštri kut jednog pravokutnog trokuta jednaki katetu i susjedni oštri kut drugog pravokutnog trokuta, tada su takvi pravokutni trokuti jednaki
3. Ako su krak i suprotni oštri kut jednog pravokutnog trokuta jednaki katetu i suprotni oštri kut drugog pravokutnog trokuta, tada su takvi pravokutni trokuti jednaki
4. Ako su hipotenuza i akutni kut jednog pravokutnog trokuta jednaki hipotenuzi i akutnom kutu drugog pravokutnog trokuta, tada su takvi pravokutni trokuti
5. Ako su kateta i hipotenuza jednog pravokutnog trokuta jednake katetu i hipotenuzi drugog pravokutnog trokuta, tada su takvi pravokutni trokuti jednaki
Da bi se utvrdila jednakost pravokutnih trokuta, dovoljno je znati da su dva elementa jednog trokuta jednaka dvama elementima drugog trokuta (isključujući pravi kut). To se, naravno, ne odnosi na jednakost dva ugla jednog trokuta i dva ugla drugog trokuta.
Budući da je u pravokutni trokut kut između dviju kateta je ravna linija, a bilo koja dva prava kuta su jednaka, tada iz prvog znaka jednakosti trokuta slijedi:
Ako su krakovi jednog pravokutnog trokuta jednaki krakovima drugog, tada su takvi trokuti jednaki (slika 5).
Ako su kateta i susjedni oštri kut jednog pravokutnog trokuta jednaki katetu i susjednom kutu drugog trokuta, tada su takvi trokuti jednaki (slika 6).

Razmotrimo još dva znaka jednakosti pravokutnih trokuta.

TEOREMA ... Ako su hipotenuza i oštri kut jednog pravokutnog trokuta jednaki hipotenuzi i oštrom kutu drugog trokuta, tada su takvi trokuti jednaki (slika 7).
DOKAZ. Iz svojstva 1ê § proizlazi da su u takvim trokutima dva druga oštra kuta također jednaka, stoga su trokuti jednaki u drugom kriteriju jednakosti trokuta, to jest u bočnom (hipotenuza) i dva susjedna kuta.
Q.E.D.
TEOREMA ... Ako su hipotenuza i kateta jednog pravokutnog trokuta jednaki hipotenuzi i katetu drugog trokuta, tada su takvi trokuti jednaki.
DOKAZ. Razmotrimo trokute ABC i A 1 B 1 C 1, čiji su uglovi C i C 1 ravne crte, AB \u003d A 1 B 1, BC \u003d B 1 C 1 (slika 8).

Jer< C = < C 1 , то треугольник ABC можно наложить на треугольник A 1 B 1 C 1 так, что вершина C совместится с вершиной C 1 , а стороны CA и CB наложатся соответственно на лучи C 1 A 1 и C 1 B 1 , поскольку CB = C 1 B 1 , то вершина B совместится с вершиной B 1 . Но тогда вершины A и A 1 также совместятся. В самом деле, если предположить, что точка A совместится с некоторой другой точкой A 2 луча C 1 A 1 , то получим равнобедренный треугольник A 1 B 1 A 2 , в котором углы при основании A 1 A 2 не равны (на рисунке < A 2 - острый, а < A 1 - тупой как смежный с острым углом B 1 A 1 C 1). Но это невозможно, поэтому вершины A и A 1 совместятся. Следовательно, полностью совместятся треугольники ABC A 1 B 1 C 1 , то есть они равны.
Q.E.D.
Pitagorin poučak
Njegov značaj leži u činjenici da se većina teorema geometrije može izvesti iz nje ili uz njezinu pomoć. Jedan od teorema omogućuje nam da se pobrinemo da ako su mu okomite i kose crte povučene iz točke izvan ravne crte, tada su: a) kose crte jednake ako su njihove projekcije jednake; b) onaj nagnutiji više, koji ima veliku projekciju.
Pitagorin teorem bio je prva izjava koja je povezivala duljine stranica trokuta. Tada su naučili kako pronaći duljine stranica i kutove trokuta s oštrim i tupim kutom. Nastala je cijela znanost o trigonometriji ("trigon" - na grčkom znači "trokut"). Ova je znanost pronašla primjenu u izmjeri zemljišta. Ali još ranije, uz njegovu pomoć, naučili su mjeriti zamišljene trokute na nebu, čiji su vrhovi bile zvijezde. Sada se trigonometrija čak koristi za mjerenje udaljenosti između svemirskih brodova.
Koristeći svojstva površina poligona, sada uspostavljamo izvanredan odnos između hipotenuze i kateta pravokutnog trokuta. Teorem koji ćemo dokazati naziva se Pitagorin teorem, koji je najvažniji teorem u geometriji.
Ako nam se da trokut
Pa čak i pod pravim kutom,
Tada kvadrat hipotenuze
Uvijek ćemo lako pronaći:
Kvadriramo noge,
Nalazimo zbroj stupnjeva
I to na tako jednostavan način
Doći ćemo do rezultata.
TEOREMA. U pravokutnom trokutu kvadrat hipotenuze jednak je zbroju kvadrata kateta.
DOKAZ. Razmotrimo pravokutni trokut s krakovima a, b i c (slika 9 a).

Dokažimo da je c 2 \u003d a 2 + b 2. Završimo trokut do kvadrata sa stranicama a + b, kao što je prikazano na slici (slika 9 b).
Površina takvog kvadrata sa stranicom a + b je (a + b) 2. S druge strane, ovaj kvadrat čine četiri jednaka pravokutna trokuta, čija je površina ab, i kvadrat sa stranicom c, dakle
Dakle, (a + b) 2 \u003d 2ab + c 2, odakle je c 2 \u003d a 2 + b 2.
Q.E.D.
KOROLAR 1 ... U pravokutnom trokutu bilo koja od kateta manja je od hipotenuze.
DOKAZ. Pitagorinim teoremom AB 2 \u003d AC 2 + BC 2 . Budući da je BC 2\u003e 0, tada je AC 2<АВ, То есть АС<АВ.
KOROLAR 2. Za bilo koji akutni kut b cosb<1.
DOKAZ. Po definiciji kosinusa cosb \u003d. Ali u posljedici 1 dokazano je da AC<АВ, dakle razlomak je manji od 1.
Pravokutni trokuti čije su stranice izražene u cjelobrojnim brojevima nazivaju se pitagorejski trokuti.
Može se dokazati da su krakovi a, b i hipotenuza c takvih trokuta izraženi formulama a \u003d 2kmn; b \u003d k (m2-n2); c \u003d k (m 2 + n 2), gdje su k, m i n prirodni brojevi takvi da je m\u003e n. Trokuti sa stranicama, čije su duljine jednake 3, 4, 5, nazivaju se egipatskim trokutima, budući da su bili poznati još Egipćanima.
Suprotno pitagorejskom teoremu.
Ako je kvadrat jedne stranice trokuta jednak zbroju kvadrata druge dvije stranice, tada je trokut pravokutni (znak pravokutnog trokuta).
DOKAZ.
Neka je u trokutu ABC AB 2 \u003d AC 2 + BC 2. Dokažimo da je kut C ravna crta. Razmotrimo pravokutni trokut A 1 B 1 C 1 s pravim kutom C 1, u kojem je A 1 C 1 \u003d AC i B 1 C 1 \u003d BC. Pitagorinim teoremom A 1 B 1 2 \u003d A 1 C 1 2 + B 1 C 1 2, pa prema tome A 1 B 1 2 \u003d AC 2 + BC 2. Ali AC 2 + BC 2 \u003d AB 2 prema hipotezi teorema. Prema tome, A 1 B 1 2 \u003d AB 2, odakle je A 1 B 1 \u003d AB. Trokuti ABC i A 1 B 1 C 1 jednaki su na tri strane, dakle< C = < C 1 , то есть треугольник ABC прямоугольный с прямым углом C.
Q.E.D.
Pravokutni trokuti, zajedno s jednakokrakim i jednakostraničnim trokutima, zauzimaju svoje mjesto među trokutima, posjedujući poseban skup specifičnih svojstava karakterističnih samo za ovu vrstu trokuta. Razmotrimo nekoliko teorema o jednakosti pravokutnih trokuta koji će uvelike pojednostaviti rješenje nekih problema.
Prvi znak jednakosti pravokutnih trokuta
Znakovi jednakosti pravokutnih trokuta proizlaze iz tri znaka jednakosti trokuta, ali pravi kut ih iskrivljuje, proširujući i olakšavajući. Bilo koji od znakova jednakosti pravokutnih trokuta može se zamijeniti jednim od tri glavna, ali to će potrajati predugo, pa je identificirano 5 svojstava i znakova jednakosti pravokutnih trokuta.
Vrlo često, umjesto korištenja osnovnih znakova jednakosti trokuta, koristi se metoda superpozicije, kada se dvije figure mentalno naslažu jedna na drugu. To ne znači da je ovo istina ili laž. Samo još jedan dokaz koji treba razmotriti. Ali ne treba misliti da se bilo koja značajka može dokazati uobičajenom superpozicijom. Zbog toga ćemo dokaz kriterija za jednakost pravokutnih trokuta razmotriti kroz tri glavna kriterija za jednakost trokuta.
Prvi znak jednakosti pravokutnih trokuta kaže: dva pravokutna trokuta jednaka su ako su dvije katete jednog trokuta jednake dvjema katetama drugog trokuta. Ukratko, ta se značajka naziva jednakost u dvije noge.

Lik: 1. Jednakost u dvije noge
Vrlo je lako dokazati ovaj znak. Dano: dvije katete pravokutnih trokuta jednake su. Između nogu postoji pravi kut, koji iznosi 90 stupnjeva, što znači da se kut trokuta podudara. Stoga su dva trokuta jednaka na dvije stranice i kut između njih.
Drugi znak
Drugi znak glasi ovako: dva pravokutna trokuta jednaka su ako su krak i susjedni oštri kut jednog trokuta jednaki kraku i susjednom kutu drugog trokuta.
Drugi se kriterij dokazuje na temelju iste izjave o međusobnoj jednakosti pravokutnih kutova. Ako su krakovi trokuta jednaki, oštri kutovi za njih su jednaki i pravi kutovi po definiciji jednaki, tada su takvi trokuti jednaki drugom znaku jednakosti (bočna i dva ugla uz nju).
Treći znak
Dva pravokutna trokuta jednaka su ako su krak i suprotni oštri kut jednaki.

Lik: 2. Crtanje za dokaz
Akutni kutovi u trokutu zbrajaju se do 90 stupnjeva. Označimo kutove malim latiničnim slovima radi jednostavnosti dokazivanja. Jedan kut je ravna linija, a druga dva ćemo označiti slovima a i b u prvom trokutu; c i d u drugom trokutu.
Kutovi a i d jednaki su međusobno prema tvrdnji problema.
Oduzmite kut a s obje strane izraza
Odnosno, ako su dva oštra kuta u dva pravokutna trokuta jednaka međusobno, tada će i druga dva oštra kuta biti jednaka, a mi možemo koristiti drugu značajku.
U drugom i trećem znaku trebate se posebno usredotočiti na akutni kut, jer su pravi kutovi uvijek međusobno jednaki.
Četvrti znak
Ako su hipotenuza i oštri kut jednog pravokutnog trokuta jednaki hipotenuzi i kutu drugog pravokutnog trokuta, tada su takvi trokuti jednaki.
Kao što je spomenuto u prethodnom znaku: ako je oštri kut pravokutnog trokuta jednak odgovarajućem oštrom kutu drugog pravokutnog trokuta, tada će drugi par oštrih kutova trokuta biti međusobno jednaki.
To znači da prema uvjetima ove značajke imamo jednakost hipotenuze i dva oštra kuta trokuta, što znači da će takvi trokuti biti jednaki u bočnom i dva susjedna kuta (2 znak jednakosti trokuta)
Peti znak
Ako su hipotenuza i kateta jednog pravokutnog trokuta jednaki hipotenuzi i katetu drugog trokuta, tada su takvi trokuti jednaki.
Ako su hipotenuza i kateta dvaju trokuta jednaki, tada će drugi krakovi takvih trokuta biti međusobno jednaki. To proizlazi iz pitagorejskog teorema.

Lik: 3. Jednakost u nozi i hipotenuzi
Kvadrat hipotenuze jednak je zbroju kvadrata kateta. Hipotenuze su jednake jedna drugoj, krak jednog trokuta jednak je kvadratu drugog trokuta, što znači da zbroj ostaje točan, a ostale dvije katete bit će jednake.
Što smo naučili?
Dokaz pet testova jednakosti trokuta razmatrali smo kroz osnovne testove jednakosti trokuta. Shvatili smo zašto je takav dokaz poželjniji za prekrivanje i utvrdili način dokaza koji će omogućiti da se u bilo kojem trenutku obnove osnovni koncepti teme u memoriji, bez pretjeranog pamćenja.
Test po temi
Članak ocjena
Prosječna ocjena: 4.6. Ukupan broj ocjena: 100.
Podsjetimo iz materijala prethodne lekcije, pravokutni trokut naziva se trokut ako ima barem jedan od kutova ravne crte (odnosno jednak je 90 o).
Smatrati prvi znakjednakost trokuta: ako su dva kraka jednog pravokutnog trokuta jednaka dvama krakovima drugog pravokutnog trokuta, tada su takvi trokuti jednaki.
Ilustrirajmo ovaj slučaj:
Lik: 1. Jednaki pravokutni trokuti
Dokaz:
Prisjetimo se prve jednakosti proizvoljnih trokuta.

Lik: 2
Ako su dvije stranice i kut između njih jednog trokuta i odgovarajuće dvije stranice i kut između njih drugog trokuta jednaki, tada su ti trokuti jednaki. To govori prvi znak jednakosti trokuta, to jest:

Sličan dokaz slijedi za pravokutne trokute:
 .
.
Trokuti su u prvom redu jednaki.
Razmotrimo drugi znak jednakosti pravokutnih trokuta. Ako su kateta i susjedni oštri kut jednog pravokutnog trokuta jednaki katetu i susjedni oštri kut drugog pravokutnog trokuta, tada su takvi trokuti jednaki.

Lik: 3
Dokaz:

Lik: četiri
Upotrijebimo drugi znak jednakosti trokuta:

Sličan dokaz za pravokutne trokute:

Trokuti su jednaki u drugom atributu.
Razmotrimo treći znak jednakosti pravokutnih trokuta: ako su hipotenuza i susjedni kut jednog pravokutnog trokuta jednaki hipotenuzi i susjednom kutu drugog trokuta, tada su takvi trokuti jednaki.
Dokaz:

Lik: pet
Prisjetimo se drugog znaka jednakosti trokuta:

Lik: 6
Ti su trokuti jednaki ako:

Budući da je poznato da je jedan par oštrih kutova u pravokutnim trokutima jednak (∠A \u003d ∠A 1), jednakost drugog para kutova (∠B \u003d ∠B 1) dokazuje se na sljedeći način:
Budući da je AB \u003d A 1 B 1 (prema uvjetu), ∠B \u003d ∠B 1, ∠A \u003d ∠A 1. Prema tome, trokuti ABC i A 1 B 1 C 1 jednaki su u drugom atributu.
Razmotrimo sljedeći kriterij za jednakost trokuta:
Ako su kateta i hipotenuza jednog trokuta jednake katetu i hipotenuzi drugog trokuta, takvi su pravokutni trokuti jednaki.

Lik: 7
Dokaz:
Zamijenimo trokute ABC i A 1 B 1 C 1. Pretpostavimo da su vrhovi A i A 1, kao i C i C 1 prekriveni, a vrh B i točka B 1 ne podudaraju se. Taj je slučaj naznačen na sljedećoj slici:

Lik: 8
U ovom slučaju možemo primijetiti jednakokračni trokut ABB 1 (po definiciji - prema uvjetu AB \u003d AB 1). Prema tome, prema svojstvu, ∠AB 1 B \u003d ∠ABB 1. Razmotrite definiciju vanjskog kuta. Vanjski kut trokutom naziva se kut uz bilo koji kut trokuta. Njegova mjera stupnja jednaka je zbroju dvaju kutova trokuta koji mu nisu susjedni. Slika prikazuje ovaj omjer:

Lik: 9
Kut 5 je vanjski kut trokuta i jednak je ∠5 \u003d ∠1 + ∠2. Stoga slijedi da je vanjski kut veći od svakog od kutova koji mu nisu susjedni.
Dakle, ∠ABB 1 je vanjski kut za trokut ABC i jednak je zbroju ∠ABB 1 \u003d ∠CAB + ∠ACB \u003d ∠ABS \u003d ∠CAB + 90 o. Dakle, ∠AV 1 V (što je oštri kut u pravokutnom trokutu ABB 1) ne može biti jednak kutu ∠AVV 1, jer je taj kut tup, što je dokazano.
To znači da se naša pretpostavka u vezi s položajem točaka B i B 1 pokazala netočnom, stoga se te točke podudaraju. Dakle, postavljeni su trokuti ABC i A 1 B 1 C 1. Stoga su jednaki (po definiciji).
Dakle, ti se znakovi ne uvode uzalud, jer se njima mogu riješiti neki problemi.
- Državno sveučilište u Omsku ().
- Portal za pomoć calc.ru ().
- Učiteljski portal ().
1. № 38. Butuzov VF, Kadomtsev SB, Prasolov VV, ur. Sadovnichy VA Geometry 7. M.: Education. 2010
2. Na temelju podataka prikazanih na slici, naznačite jednake trokute, ako postoje.

3. Na temelju podataka prikazanih na slici, naznačite jednake trokute, ako postoje. Imajte na umu da je AC \u003d AF.

4. U pravokutnom trokutu medijan i visina se povlače prema hipotenuzi. Kut između njih je 20 °. Odredite veličinu svakog od oštrih kutova ovog pravokutnog trokuta.
Odjeljci: Matematika
Tema: "Znakovi jednakosti pravokutnih trokuta"
Svrha: konsolidacija znanja (svojstva pravokutnih trokuta), upoznavanje s nekim znakovima jednakosti pravokutnih trokuta.
Tijekom nastave:
I. Organizacijski trenutak.II. Oralno.
1. Odgovorite na pitanja:
- Navedi elemente pravokutnog trokuta.
- Koja su svojstva elemenata pravokutnog trokuta?
- Dokazati da je krak pravokutnog trokuta koji leži nasuprot kutu od 30 0 jednak polovici hipotenuze.
- Dokazati da je ako je krak pravokutnog trokuta polovica hipotenuze, tada je kut nasuprot ovom kraku 30 0.
- Pronađi x. Odaberite odgovor iz trokuta. Slova riječi nalaze se u sektorima trokuta. Rasprava u paru (3 min).
Slika 1.
Oni su izmislili riječ "znak".
III. Učenje novog gradivaProučavajući trokute, kažemo da on ima neka svojstva i karakteristike. A koje znakove jednakosti trokuta znate? Formulirali smo i dokazali svojstva pravokutnih trokuta, a danas ćemo razmotriti znakove jednakosti pravokutnih trokuta, rješavati probleme koristeći ih.
Dokazujući jednakost trokuta, koliko je parova pronađeno odgovarajuće jednakih elemenata? Je li moguće dokazati jednakost pravokutnih trokuta u dvije katete?
Prije nego što ste dva pravokutna trokuta ABC i A 1 B 1 C 1, noge su im jednake. Dokažite, ako je moguće, njihovu jednakost.
# 1. (Na dvije noge)

Slika 2.
Dano: ABC i A 1 B 1 C 1, B \u003d B 1 \u003d 90 0, AB \u003d A 1 B 1, BC \u003d B 1 C 1
Dokazati: ABC \u003d A 1 B 1 C 1
Kako će zvučati znak? (Zatim zadatak br. 1)
# 2. (Uz nogu i oštri kut uz nju)

Slika 3.
Dano: ABC i A 1 B 1 C 1, B \u003d B 1 \u003d 90 0, BC \u003d B 1 C 1, C \u003d C 1
Dokazati: ABC \u003d A 1 B 1 C 1
Kako će zvučati znak? (Zatim zadatak broj 2)
Broj 3. (Hipotenuzom i akutnim kutom)

Slika 4.
Dano: ABC i A 1 B 1 C 1, B \u003d B 1 \u003d 90 0, AC \u003d A 1 C 1, A \u003d A 1
Dokazati: ABC \u003d A 1 B 1 C 1
Kako će zvučati znak? (Zatim zadatak broj 3)
Zadaci. Pronađite jednake trokute i dokažite njihovu jednakost.

Slika 5.
IV. Učvršćivanje naučenog u lekciji.Riješite sljedeći problem.

Slika 6.
Dano: ABC, A 1 B 1 C 1, DAB \u003d CBA \u003d 90 0, AD \u003d BD
Dokazati: CAB \u003d DBA.
Rasprava u četverac (3 min).
Zašto je zadatak iz udžbenika # 261 sa zapisom.

Slika 7.
Dano: ABC - jednakokraka, AD i CE - visina ABC
Dokazati: AD \u003d CE
Dokaz:
V. Dodjela kod kuće.
P.35 (tri znaka), # 261 (da bi dokazao da je AOS jednakokračan), # 268 (znak jednakosti pravokutnih trokuta uzduž katete i suprotnog kuta).
U sljedećoj lekciji iz geometrije nastavit ćemo upoznavanje sa znakovima jednakosti pravokutnih trokuta. Sljedeći ću put također staviti ocjene na rezultate 2 lekcije.
Dodatno. Pronađite jednake trokute.