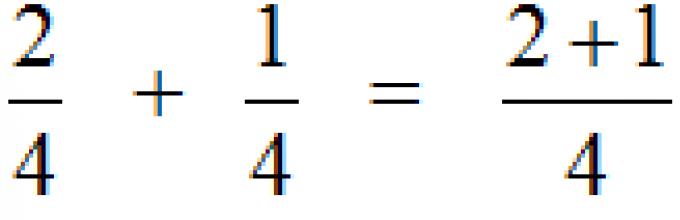Aggiunta di frazioni con gli stessi denominatori
L'aggiunta di frazioni è due tipi:
- Aggiunta di frazioni con gli stessi denominatori
- Aggiunta di frazioni S. denominatore diverso.
Per prima cosa studiamo l'aggiunta di frazioni con gli stessi denominatori. Tutto è semplice qui. Per piegare le frazioni con gli stessi denominatori, è necessario piegare i loro numeri e il denominatore è lasciato invariato. Ad esempio, piegare le frazioni e. Piegheremo i numeri e il denominatore è lasciato invariato:

Questo esempio può essere facilmente compreso se ricordi della pizza, che è divisa in quattro parti. Se aggiungi la pizza alla pizza, la pizza sarà:

ESEMPIO 2. Piega le frazioni e.

In risposta, ha scoperto la frazione sbagliata. Se arriva la fine del compito, quindi dalle frazioni sbagliate è consuetudine sbarazzarsi di. Per sbarazzarsi della frazione sbagliata, è necessario evidenziare l'intera parte in esso. Nel nostro caso, l'intera parte si distingue facilmente - due suddivisi in due uguali:

Questo esempio può essere facilmente compreso se ricordi della pizza, che è divisa in due parti. Se la pizza viene aggiunta alla pizza, allora un'intera pizza sarà:

ESEMPIO 3.. Piega le frazioni e.
Di nuovo, pieghiamo i numeri e il denominatore è lasciato invariato:
![]()
Questo esempio può essere facilmente compreso se ricordi della pizza, che è divisa in tre parti. Se la pizza viene aggiunta alla pizza, allora la pizza sarà:

ESEMPIO 4. Trova un valore di espressione 
Questo esempio è risolto già come quelli precedenti. I numeri devono essere piegati e il denominatore è lasciato invariato:
Proviamo a ritrarre la nostra soluzione usando l'immagine. Se aggiungi la pizza alla pizza e aggiungi pizza, allora si rivelerà 1 intero e pizza.

Come puoi vedere in aggiunta di frazioni con gli stessi denominanti, non c'è niente di complicato. È sufficiente capire le seguenti regole:
- Per piegare le frazioni con lo stesso denominatore, è necessario aggiungere i loro numeri e il denominatore è lasciato invariato;
Aggiunta di frazioni con diversi denominatori
Ora impari come mettere una frazione con diversi denominatori. Quando le frazioni sono piegate, i denominatori di queste fronains dovrebbero essere uguali. Ma non sono sempre gli stessi.
Ad esempio, le frazioni possono essere piegate, poiché hanno gli stessi denominatori.
Ma i fraci e aggiungono immediatamente impossibile, perché queste fronaci hanno diversi denominatori. In tali casi, il Fraci deve portare allo stesso valore (generale) denominatore.
Ci sono diversi modi per portare le frazioni allo stesso denominatore. Oggi considereremo solo uno di loro, dal momento che i metodi rimanenti possono sembrare complessi per principianti.
L'essenza di questo metodo è che è prima per la prima ricerca di (NOC) denominatori di entrambe le frazioni. Quindi il NOC è diviso in un denominatore della prima frazione e ottiene il primo fattore aggiuntivo. È simile e con la seconda frazione - il NOC è diviso in un denominatore della seconda frazione e riceve un secondo fattore aggiuntivo.
Quindi i numeri e i denominatori di frazioni sono moltiplicati per i loro fattori aggiuntivi. Come risultato di queste azioni, le cui frazioni erano diversi denominatori, trasformano in una frazione che hanno gli stessi denominatori. E come piegare le frazioni tali, lo sappiamo già.
Esempio 1.. Spostando il fraci I.
Prima di tutto, troviamo i più piccoli denominatori multipli di entrambe le frazioni. Il denominatore della prima frazione è il numero 3 e il denominatore della seconda frazione - un numero 2. Il più piccolo multiplo totale di questi numeri è 6
NOK (2 e 3) \u003d 6
Ora torniamo a frazioni e. All'inizio ci dividiamo il NOC sul denominatore della prima frazione e ottieni il primo fattore aggiuntivo. NOC è il numero 6, e il denominatore della prima frazione è il numero 3. Delim 6-3, otteniamo 2.
Il numero 2 risultante è il primo fattore aggiuntivo. Scrivilo alla prima frazione. Per fare questo, facciamo una piccola linea obliqua sulla frazione e scriviamo un fattore aggiuntivo trovato sopra:
Allo stesso modo, facciamo con la seconda frazione. Dividiamo il NOC al denominatore della seconda frazione e otteniamo il secondo fattore opzionale. NOC è il numero 6 e il denominatore di seconda frazione è un numero 2. Delim 6 a 2, otteniamo 3.
Il numero 3 risultante è il secondo fattore opzionale. Scrivilo alla seconda frazione. Ancora una volta, facciamo una piccola linea obliqua sulla seconda frazione e scrivi un fattore opzionale rilevato sopra:
Ora tutto è pronto per la dipendenza. Resta per moltiplicare i numeri e i denominatori di frazioni sui loro fattori aggiuntivi:

Guarda attentamente ciò che siamo arrivati. Siamo arrivati \u200b\u200bal fatto che le frazioni di cui avevano diversi denominatori, trasformati in una frazione in cui gli stessi denominatori. E come piegare le frazioni tali, lo sappiamo già. Facciamo questo esempio alla fine:

Pertanto, l'esempio è completato. Per aggiungerlo si scopre.
Proviamo a ritrarre la nostra soluzione usando l'immagine. Se aggiungi pizza alla pizza, allora un'intera pizza arriverà e un'altra sesta pizza:

Portare le frazioni allo stesso denominatore (condiviso) può anche essere raffigurato utilizzando un'immagine. Riferendando una frazione e un denominatore comune, abbiamo avuto una frazione e. Queste due frazioni saranno rappresentate con gli stessi pezzi di pizza. La differenza sarà solo che questa volta saranno divisi in azioni identiche (sono mostrate allo stesso denominatore).

Il primo disegno raffigura una frazione (quattro pezzi di sei), e il secondo disegno raffigura una frazione (tre pezzi di sei). Piegare questi pezzi otteniamo (sette pezzi di sei). Questa frazione non è corretta, quindi abbiamo assegnato l'intera parte in esso. Di conseguenza, hanno ricevuto (una pizza intera e un'altra sesta pizza).
Nota che abbiamo dipinto questo esempio troppo dettagliato. NEL istituzioni educative Non accettato per scrivere così esploso. Devi essere in grado di trovare rapidamente la NIC dei Denominatori e dei guasti aggiuntivi a loro, oltre a moltiplicare rapidamente i guasti aggiuntivi trovati sui propri numeri e denominatori. Essendo a scuola, questo esempio dovrebbe essere scritto come segue:

Ma ce n'è I. lato posteriore Medaglie. Se alle prime fasi dello studio della matematica non effettuare record dettagliati, le domande iniziano ad apparire "E da dove viene?", "Perché la Fraraty si trasforma improvvisamente in un'altra frazione? «.
Per rendere più facile aggiungere frazioni con diversi denominatori, è possibile utilizzare le seguenti istruzioni passo passo:
- Trovare le frazioni NOK Rannels;
- Dividere il NOC al denominatore di ogni frazione e ottenere un fattore aggiuntivo per ogni frazione;
- Moltiplicare i numeri e i denominatori di frazioni sui loro fattori aggiuntivi;
- Piega le frazioni che hanno gli stessi denominatori;
- Se la risposta si è rivelata essere una frazione impropria, quindi si distingue da una parte intera;
ESEMPIO 2. Trova un valore di espressione  .
.
Usiamo le istruzioni fornite sopra.
Passaggio 1. Trova le frazioni NOK Rannels
Troviamo il NOC dei denominatori di entrambe le frazioni. Dannels of fractions sono numeri 2, 3 e 4

Passaggio 2. Per dividere il NOC al denominatore di ogni frazione e ottenere un ulteriore fattore per ogni frazione
Delim NOK al denominatore della prima frazione. NOK è un numero 12 e il denominatore della prima frazione è il numero 2. Delim 12 a 2, otteniamo 6. ha ricevuto il primo fattore aggiuntivo 6. lo scriviamo sopra la prima frazione:
Ora dividi il NOK al firmatario della seconda frazione. NOK è un numero 12 e la seconda frazione Denominator è il numero 3. Delive da 12 a 3, otteniamo 4. Ha ricevuto il secondo Factory Factory 4. Scrivilo sulla seconda frazione:
Ora dividiamo il NOC al denominatore della terza frazione. NOK è un numero 12 e il denominatore della terza frazione è il numero 4. Delim 12-4, otteniamo 3. ricevuto il terzo fattore aggiuntivo 3. Registralo oltre la terza frazione:
Passaggio 3. Moltiplicare i numeri e i denominatori di frazioni sui loro fattori aggiuntivi
Moltiplichiamo i numeri e i denominatori sui loro fattori aggiuntivi:
Passaggio 4. Piegare le frazioni in cui gli stessi denominanti
Siamo arrivati \u200b\u200bal fatto che le frazioni di cui avevano diversi denominatori, trasformati in una frazione, che hanno lo stesso (generale) denominatori. Resta per piegare queste frazioni. Pieghiamo:

L'aggiunta non è adattata su una riga, quindi abbiamo spostato l'espressione rimanente alla riga successiva. È permesso in matematica. Quando l'espressione non si adatta per una linea, viene trasferita alla riga successiva ed è necessario mettere il segno di uguaglianza (\u003d) alla fine della prima riga e all'inizio della nuova riga. Il segno uguale sulla seconda linea suggerisce che questa è una continuazione dell'espressione che era sulla prima riga.
Passaggio 5. Se lo scatto sbagliato si è scoperto nella risposta, quindi allocare l'intera parte in esso
La nostra risposta si è rivelata sbagliata. Dobbiamo evidenziare l'intera parte. Evidenziamo:

Ricevuto la risposta
Sottrarre le frazioni con gli stessi denominatori
La sottrazione di frazioni avviene due tipi:
- Sottrarre le frazioni con gli stessi denominatori
- Sottrazione di frazioni con diversi denominatori
Per prima cosa studiamo la sottrazione di frazioni con gli stessi denominatori. Tutto è semplice qui. Per sottrarre da una frazione un altro, è necessario trovare il numeratore di seconda frazione dal numero della prima frazione e il denominatore è lasciato per lo stesso.
Ad esempio, trova il valore dell'espressione. Per risolvere questo esempio, è necessario sottrarre il numeratore di seconda frazione dal numero della prima frazione e il denominatore è lasciato invariato. E fallo:

Questo esempio può essere facilmente compreso se ricordi della pizza, che è divisa in quattro parti. Se tagli la pizza dalla pizza, allora la pizza sarà:

ESEMPIO 2. Trova il valore dell'espressione.
Ancora una volta, dal numero della prima frazione, sottraiamo il secondo numeratore di frazione e il denominatore è lasciato invariato:

Questo esempio può essere facilmente compreso se ricordi della pizza, che è divisa in tre parti. Se tagli la pizza dalla pizza, allora la pizza sarà:

ESEMPIO 3. Trova un valore di espressione 
Questo esempio è risolto già come quelli precedenti. Dal numeratore della prima frazione è necessario sottrarre le impostazioni delle altre frazioni:

Come puoi vedere nella sottrazione di frazioni con gli stessi denominatori non c'è niente di complicato. È sufficiente capire le seguenti regole:
- Per sottrarre da una frazione un altro, è necessario sottrarre il numero della seconda frazione dal numero della prima frazione, e il denominatore è lasciato invariato;
- Se la risposta si è rivelata essere frazione impropria, è necessario evidenziare l'intera parte.
Sottrazione di frazioni con diversi denominatori
Ad esempio, la frazione può essere sottratta, poiché queste frazioni hanno gli stessi denominatori. Ma la frazione non può essere sottratta, poiché queste fronacini hanno diversi denominatori. In tali casi, il Fraci deve portare allo stesso valore (generale) denominatore.
Il Denominatore Generale trova sullo stesso principio che abbiamo usato quando aggiungiamo frazioni con diversi denominatori. Prima di tutto, trovano il NOC dei denominatori di entrambe le frazioni. Quindi il NOC è diviso in un denominatore della prima frazione e riceve il primo fattore aggiuntivo, che è registrato sopra la prima frazione. Allo stesso modo, NOC sono suddivisi in un denominatore della seconda frazione e ricevono un secondo fattore aggiuntivo, che è registrato sopra la seconda frazione.
Quindi la frarata è moltiplicata per i loro fattori aggiuntivi. Come risultato di queste operazioni, le cui frazioni avevano diversi denominatori, trasformano in una frazione che hanno gli stessi denominatori. E come dedurre tali frazioni che già conosciamo.
Esempio 1. Trova il valore dell'espressione:
Questi frinati hanno diversi denominatori, quindi è necessario portarli allo stesso valore (generale) denominatore.
Per prima cosa troviamo il NOC dei denominatori di entrambe le frazioni. Il denominatore della prima frazione è il numero 3, e il denominatore della seconda frazione è il numero 4. Il più piccolo multiplo totale di questi numeri è 12
NOK (3 e 4) \u003d 12
Ora torniamo a frazioni e
Trova un fattore aggiuntivo per la prima frazione. Per fare ciò, dividiamo il NOC sul denominatore della prima frazione. NOK è un numero 12 e il denominatore della prima frazione - il numero 3. Delim 12 a 3, otteniamo 4. Scrivi il quarto sopra la prima frazione:
Allo stesso modo, facciamo con la seconda frazione. Dividiamo il NOC al denominatore della seconda frazione. NOC è il numero 12 e il denominatore della seconda frazione è il numero 4. Delim 12 a 4, otteniamo 3. Scrivi i primi tre sopra la seconda frazione:
Ora tutto è pronto per la sottrazione. Resta per moltiplicare la frazione sui suoi fattori aggiuntivi:

Siamo arrivati \u200b\u200bal fatto che le frazioni di cui avevano diversi denominatori, trasformati in una frazione in cui gli stessi denominatori. E come dedurre tali frazioni che già conosciamo. Facciamo questo esempio alla fine:

Ricevuto la risposta
Proviamo a ritrarre la nostra soluzione usando l'immagine. Se tagli la pizza dalla pizza, allora ci sarà la pizza

Questa è una versione dettagliata della soluzione. Mentre a scuola, dovremmo risolvere questo esempio più corto. Sembrerebbe una soluzione così come segue:

Portare frazioni e un denominatore condiviso può anche essere raffigurato utilizzando un'immagine. Abbassando queste frazioni al Denominatore Generale, abbiamo avuto una frazione e. Queste frazioni saranno raffigurate con gli stessi pezzi di pizza, ma questa volta saranno suddivisi in azioni identiche (sono mostrate allo stesso denominatore):

Il primo disegno raffigura una frazione (otto pezzi di dodici) e il secondo disegno - frazione (tre pezzi di dodici). Ho tagliato da otto pezzi tre pezzi riceviamo cinque pezzi di dodici anni. Frazione e descrive questi cinque pezzi.
ESEMPIO 2. Trova un valore di espressione 
Queste frazioni hanno diversi denominatori, quindi devi prima portarli allo stesso (generale) denominatore.
Troviamo il NOC dei denominatori di queste fronains.
Rannoni di frazioni Questi sono i numeri 10, 3 e 5. Il più piccolo multiplo totale di questi numeri è 30
NOK (10, 3, 5) \u003d 30
Ora troviamo moltiplicatori aggiuntivi per ogni frazione. Per fare ciò, dividiamo il NOC al denominatore di ogni frazione.
Trova un fattore aggiuntivo per la prima frazione. NOK è il numero 30, e il denominatore della prima frazione è il numero 10. Dividiamo da 30 a 10, otteniamo il primo fattore aggiuntivo 3. Registralo sulla prima frazione:
Ora troviamo un fattore aggiuntivo per la seconda frazione. Dividiamo il NOC sul firmatario della seconda frazione. NOC è un numero 30 e il canale della seconda frazione è il numero 3. Delim 30 a 3, otteniamo il secondo fattore opzionale 10. Lo scriviamo sulla seconda frazione:
Ora troviamo un fattore aggiuntivo per la terza frazione. Dividiamo il NOC sul denominatore della terza frazione. NOC è il numero 30 e il denominatore della terza frazione è il numero 5. Delim 30 a 5, otteniamo il terzo fattore aggiuntivo 6. La scriviamo sulla terza frazione:
Ora tutto è pronto per la sottrazione. Resta per moltiplicare la frazione sui suoi fattori aggiuntivi:
Siamo arrivati \u200b\u200bal fatto che il cui inquadratura aveva diversi denominatori, trasformato in una frazione in cui gli stessi denominatori (generali). E come dedurre tali frazioni che già conosciamo. Facciamo questo esempio.
La continuazione dell'esempio non si adatta a una linea, quindi trasferiamo la continuazione alla riga successiva. Non dimenticare il segno di uguaglianza (\u003d) sulla nuova riga:

La risposta ha scoperto la frazione giusta, e sembra che tutto ci vada, ma è troppo ingombrante e brutta. Sarebbe necessario renderlo più facile. E cosa può essere fatto? Puoi tagliare questa frazione.
Per ridurre la frazione, è necessario dividere il suo numeratore e il suo denominatore su numeri (NOD)) 20 e 30.
Quindi, troviamo i nodi dei numeri 20 e 30:

Ora torniamo al nostro esempio e dividiamo il numeratore e il denominatore della frazione sul nodo trovato, cioè a 10

Ricevuto la risposta
Moltiplicazione di frazioni per numero
Per moltiplicare la frazione da parte del numero, è necessario un numeratore di questa frazione da moltiplicare su questo numero, e il denominatore è lasciato invariato.
Esempio 1.. Moltiplicare la frazione al numero 1.
Moltiplicare il cranistro numero 1
![]()
La registrazione può essere compresa come richiedere la metà 1 volta. Ad esempio, se la pizza prendere 1 volta, allora ci sarà la pizza

Dalle leggi della moltiplicazione, sappiamo che se il moltiplicatore e il moltiplicatore vengono modificati in luoghi, il lavoro non cambierà. Se l'espressione, scrivi, allora il lavoro sarà comunque uguale. Ancora una volta, la regola di moltiplicare il numero intero e la frazione è attivata:
![]()
Questa voce può essere intesa come la cattura della metà da una. Ad esempio, se c'è 1 pizza intera e prenderemo la metà da esso, allora avremo la pizza:

ESEMPIO 2.. Trova un valore di espressione
Moltiplicare il numeratore del frantoio su 4
![]()
In risposta, ha scoperto la frazione sbagliata. Evidenziamo l'intera parte in esso:
![]()
L'espressione può essere intesa come la cattura di due trimestri 4 volte. Ad esempio, se la pizza prende 4 volte, allora otterrai due pizza intera

E se cambi il moltiplicatore al moltiplicatore, avremo l'espressione. Sarà anche uguale a 2. Questa espressione può essere intesa come la cattura di due pizza da quattro pizze intere:

Il numero che viene moltiplicato per la frazione e il denominatore della frazione è consentito se hanno un divisore comune, un'unità maggiore.
Ad esempio, l'espressione può essere calcolata in due modi.
Primo metodo. Moltiplicare il numero 4 sul numeratore di Fluster e il Denomote Denomotore di lasciare invariato:
![]()
Secondo via. Il quarto moltiplicatore e il quarto, che è nel denoter, può essere ridotto. Puoi tagliare questi quattro, dal momento che il più grande divisor comune per due quarti è la quarta piastra:

È uscito lo stesso risultato 3. Dopo aver tagliato il quarto, i nuovi numeri sono formati al loro posto: due unità. Ma moltiplicando l'unità con i primi tre, quindi la divisione per unità non cambia nulla. Pertanto, la soluzione può essere scritta più breve:
La riduzione può essere eseguita anche quando abbiamo deciso di utilizzare il primo metodo, ma allo stadio di moltiplicazione del numero 4 e del numeratore 3, abbiamo deciso di sfruttare la riduzione:

Ma ad esempio, l'espressione può essere calcolata solo nel primo modo - moltiplicare 7 al denimoter della frazione e il denominatore non è cambiato:
![]()
Ciò è dovuto al fatto che il numero 7 e il denominatore della frazione non dispongono di un divisore comune, la maggior parte dell'unità e non sono ridotti di conseguenza.
Alcuni studenti per errore riducono il numero moltiplicato e il numeratore di Fluster. È impossibile farlo. Ad esempio, la prossima voce non è corretta:
Ridurre la frazione lo implica e numeratore e denominatore sarà diviso nello stesso numero. In una situazione con l'espressione, la divisione è stata eseguita solo nel numeratore, poiché è notato che è come scrivere. Vediamo che la divisione è fatta solo nel numeratore e nel denominatore non si verifica.
Moltiplicazione di frazioni
Per moltiplicare le frazioni, è necessario moltiplicare i loro numeri e denominatori. Se la risposta è sbagliata, la frantumazione è possibile, è necessario evidenziare l'intera parte in esso.
Esempio 1. Trova il valore dell'espressione.
![]()
Ha ricevuto una risposta È consigliabile ridurre questa frazione. La frazione può essere ridotta di 2. Quindi la soluzione finale prenderà il seguente modulo:

L'espressione può essere intesa come la presa della pizza dalla metà della pizza. Supponiamo di avere metà pizza:
Come prendere due terzi da questo mezzo? Per prima cosa devi dividere questa metà in tre parti uguali:

E prendi due pezzi da questi tre pezzi:

Avremo la pizza. Ricorda come appare la pizza, divisa in tre parti:

Un pezzo da questa pizza e i due pezzi presi da noi avrà le stesse dimensioni:

In altre parole, stiamo parlando della stessa pizza. Pertanto, il valore dell'espressione è uguale

ESEMPIO 2.. Trova un valore di espressione
Moltiplicare il numeratore della prima frazione sul numeratore di seconda frazione e il denominatore della prima frazione sul denominatore della seconda frazione:

In risposta, ha scoperto la frazione sbagliata. Evidenziamo l'intera parte in esso:
![]()
ESEMPIO 3. Trova un valore di espressione
Moltiplicare il numeratore della prima frazione sul numeratore di seconda frazione e il denominatore della prima frazione sul denominatore della seconda frazione:
![]()
La risposta ha scoperto la frazione corretta, ma sarà buona se lo tagli. Per ridurre questa frazione, è necessario un numeratore e un denominatore di questa frazione per dividere nel più grande divisore comune (nodo) dei numeri 105 e 450.
Quindi, trova i nodi dei numeri 105 e 450:

Ora dividi il numeratore e il denominatore della nostra risposta al nodo, che ora abbiamo trovato, cioè a 15
La rappresentazione di un numero intero sotto forma di una frazione
Qualsiasi numero intero può essere rappresentato come una frazione. Ad esempio, il numero 5 può essere rappresentato come. Da questo alard non cambia il suo valore, poiché l'espressione significa "il numero cinque per dividere da uno", e questo è noto ai primi cinque:
Numeri inversi
Ora farmo conoscere molto un argomento interessante In matematica. Si chiama "numeri inversi".
Definizione. Torna al numerouN. chiamato il numero che quando si moltiplichiuN. Dà un'unità.
Sostituire in questa definizione invece di una variabile uN. Numero 5 e prova a leggere la definizione:
Torna al numero 5 chiamato il numero che quando si moltiplichi 5 Dà un'unità.
È possibile trovare un tale numero che quando moltiplicando per 5 dà uno? Si scopre. Immagina un cinque sotto forma di una frazione:
Quindi moltiplicare questa frazione a me stesso, cambia solo il numeratore e il denominatore. In altre parole, moltiplicherò una frazione su me stesso, girò solo:
Cosa succede come risultato di questo? Se continuiamo a risolvere questo esempio, otterremo un'unità:
![]()
Quindi inverso al numero 5 è il numero, poiché quando si moltiplicando 5, viene ottenuta un'unità.
Il numero inversa può anche essere trovato per qualsiasi altro numero intero.
Puoi anche trovare l'intelligenza per qualsiasi altra frazione. Per fare questo, è sufficiente capovolgerlo.
Divisione frazione
Supponiamo di avere metà pizza:
Ci dividiamo allo stesso modo per due. Quante pizza arriverà a tutti?

Si può vedere che dopo la separazione della metà della pizza, due pezzi uguali si sono rivelati, ognuno dei quali è la pizza. Quindi tutti saliranno sulla pizza.
Ora, quando abbiamo imparato a piegarsi e moltiplicare le frazioni separate, puoi considerare disegni più complessi. Ad esempio, cosa succede se l'attività è anche dipendente e sottrazione, e moltiplicando le frazioni?
Prima di tutto, è necessario tradurre tutte le frazioni nel torto. Quindi eseguiamo costantemente le azioni richieste - nello stesso modo dei numeri convenzionali. Vale a dire:
- In primo luogo, viene aumentato in una laurea - sbarazzarsi di tutte le espressioni contenenti indicatori;
- Quindi - Divisione e moltiplicazione;
- L'ultimo passo è fatto aggiunta e sottrazione.
Naturalmente, se ci sono staffe nell'espressione, la procedura è cambiata - tutto ciò che si trova all'interno delle parentesi dovrebbe essere considerato per primo. E ricorda le frazioni sbagliate: è necessario allocare l'intera parte quando tutte le altre azioni sono già state soddisfatte.
Traduciamo tutte le frazioni dalla prima espressione con il torto, quindi eseguire azioni:

Ora trova il valore della seconda espressione. Non ci sono frazioni con una parte intera, ma ci sono parentesi, quindi per la prima volta eseguiamo l'aggiunta, e solo allora - divisione. Si noti che 14 \u003d 7 · 2. Poi:
Infine, consideriamo il terzo esempio. Ci sono parentesi e una laurea - sono meglio considerati separatamente. Dato che 9 \u003d 3 · 3, abbiamo:
Prestare attenzione all'ultimo esempio. Per costruire una frazione nella misura, è necessario separare il numeratore separatamente in questo grado e separatamente il denominatore.
Puoi risolvere in modo diverso. Se si ricorda il grado di laurea, il compito sarà ridotto alla solita moltiplicazione delle frazioni:
Frazioni multi-piano
Finora, abbiamo solo considerato le frazioni "pulite" quando il numeratore e il denominatore sono numeri ordinari. Questo corrisponde completamente alla determinazione della frazione numerica data nella prima lezione.
Ma cosa succede se in un numeratore o denominatore per posizionare un oggetto più complesso? Ad esempio, un'altra frazione numerica? Tali strutture sorgono abbastanza spesso, specialmente quando si lavora con lunghe espressioni. Ecco un paio di esempi:
La regola di lavoro con frazioni multi-store è solo una cosa: è necessario liberarli immediatamente di loro. Rimuovere i pavimenti "extra" è abbastanza semplice se si ricorda che la funzione frazionaria significa un'operazione di divisione standard. Pertanto, qualsiasi frazione può essere riscritta come segue:
Usando questo fatto e osservando la procedura, ridurremo facilmente qualsiasi frazione multi-piano alla normalità. Dai un'occhiata agli esempi:
Un compito. Traduci frazioni multi-store in normalità:
In ogni caso, riscrivi la frazione sfusa, sostituendo la funzione di separazione della divisione. Ricordiamo inoltre che qualsiasi numero intero rappresenta sotto forma di una frazione con Denominator 1. Quelli. 12 \u003d 12/1; 3 \u003d 3/1. Noi abbiamo:

NEL l'ultimo esempio Prima che la moltiplicazione finale della frazione fosse ridotta.
Specificità di lavorare con frazioni multipiano
Nelle frazioni a più piani c'è una sottigliezza che devi sempre ricordare, altrimenti è possibile ottenere una risposta errata, anche se tutti i calcoli erano corretti. Guarda:
- Il Numener è un numero separato 7 e nel denominatore - lo scatto 12/5;
- Nel numeratore c'è una frazione 7/12 e nel denominatore - un numero separato 5.
Quindi, per un record, due interpretazioni completamente diverse ricevute. Se calcolarsi, le risposte saranno anche diverse:
Per registrare sempre leggi sicuramente, utilizzare una regola semplice: la linea condivisa della frazione principale dovrebbe essere più lunga del tratto nidificato. Preferibilmente - più volte.
Se segui questa regola, le frazioni precedenti dovrebbero essere registrate come questa:
Sì, forse è brutto e prende troppo spazio. Ma considererai correttamente. Infine, un paio di esempi in cui si verificano veramente frazioni multipiano:
Un compito. Trova i valori delle espressioni:
Quindi, lavoriamo con il primo esempio. Traduciamo tutte le frazioni nel torto, quindi eseguire le operazioni di aggiunta e divisione:

Allo stesso modo, procedere con il secondo esempio. Traduciamo tutte le frazioni nel torto ed eseguiamo le operazioni richieste. Per non stancare il lettore, darò alcuni calcoli ovvi. Abbiamo:

A causa del fatto che nel numeratore e nel denominatore delle frazioni principali ci sono importi, la regola di registrazione dei frinati multi-piano viene automaticamente rispettata. Inoltre, in quest'ultimo esempio, abbiamo intenzionalmente lasciato il numero 46/1 sotto forma di una frazione per soddisfare la divisione.
Si notò inoltre che in entrambi gli esempi, una funzione frazionaria sostituisce effettivamente le staffe: la prima cosa che abbiamo trovato l'importo e solo allora sono private.
Qualcuno dirà che la transizione verso le frazioni sbagliate nel secondo esempio era chiaramente eccessiva. Forse lo è. Ma con questo assicuriamo da errori, perché la prossima volta un esempio può essere molto più complicato. Scegli te stesso, cosa più importante: velocità o affidabilità.
Moltiplicazione e divisione delle frazioni.
Attenzione!
Questo argomento ha aggiuntivo
Materiali in una sezione speciale 555.
Per coloro che sono fortemente "non molto ..."
E per coloro che sono "molto ...")
Questa operazione è molto più più bella aggiunta-sottrazione! Perché è più facile. Ti ricordo: per moltiplicare la frazione sulla frazione, è necessario moltiplicare i numeri (sarà il risultante) e i denominatori (questo sarà il denominatore). I.e:
Per esempio:

Tutto è estremamente semplice. E per favore non cercare un denominatore comune! Non ho bisogno di lui qui ...
Per dividere la frazione per la frazione, è necessario capovolgere secondo(Questa è importante!) Frazione e moltiplicali, I.e.:

Per esempio:

Se la moltiplicazione o la divisione con interi e frazioni è stato catturato - nulla di terribile. Come con l'aggiunta, facciamo una frazione con un'unità nel Denominatore - e in avanti! Per esempio:

Nelle scuole superiori, è spesso necessario affrontare Droks a tre piani (o anche a quattro piani!). Per esempio:
Come portare questa frazione a una mente decente? Sì, molto semplice! Usa la divisione in due punti:

Ma non dimenticare l'ordine della divisione! A differenza della moltiplicazione, è molto importante qui! Naturalmente, 4: 2 o 2: 4 Non siamo confusi. Ma nella frazione a tre piani è facile commettere un errore. Nota, ad esempio:
Nel primo caso (espressione a sinistra):

Nel secondo (espressione a destra):

Senti la differenza? 4 e 1/9!
E qual è l'ordine della divisione? O parentesi o (come qui) la lunghezza delle linee orizzontali. Sviluppa il contatore degli occhi. E se non ci sono parentesi, né dash, come:
quindi dividere-moltiplicare in alcuni, a sinistra a destra!
E una tecnica molto semplice e importante. Nelle azioni con lauree, lui oh, come posso rimanere utile! Dividiamo l'unità a qualsiasi frazione, ad esempio, entro il 13/12:

La frazione si è rivolta! E succede sempre. Quando si divide 1 a qualsiasi frazione, di conseguenza, otteniamo la stessa frazione solo invertita.
Questa è tutte le azioni con frazioni. La cosa è abbastanza semplice, ma gli errori danno più che abbastanza. Nota consiglio praticoE i loro (errori) saranno meno!
Suggerimenti pratici:
1. La cosa più importante quando si lavora con le espressioni frazionarie è accuratezza e attenzione! Non è parole generali, non auguri! Questo è un duro bisogno! Tutti i calcoli sull'esame rendono come un compito completo, concentrandosi e chiaramente. È meglio scrivere due linee extra nella bozza, che accumularsi quando si calcola la mente.
2. Negli esempi con specie diverse Frazioni - Vai alle frazioni ordinarie.
3. Tutte le frazioni tagliano finché non si arresta.
4. Le espressioni frazionate a più piani sono ridotte a ordinarie, utilizzando la divisione in due punti (seguire l'ordine della divisione!).
5. Unità di frazione divide in mente, basta girare la frazione.
Ecco i compiti che devi rompere. Le risposte vengono fornite dopo tutte le attività. Utilizzare i materiali di questo argomento e consigli pratici. Conta quanti esempi potresti risolvere correttamente. La prima volta! Senza una calcolatrice! E fai conclusioni fedeli ...
Ricorda: la risposta corretta, il risultato derivante dal secondo (ancora di più - il terzo) volte - non considerato! Tale è una dura vita.
Così, decidiamo nella modalità di esame ! Questo è già preparato per l'esame, a proposito. Risolviamo l'esempio, controllare, risolvere quanto segue. Hanno deciso tutto - hanno controllato di nuovo dal primo a durare. Solo dopo Guardiamo le risposte.
Calcolare:


Hai tagliato?
Stiamo cercando risposte che coincidono con i tuoi. Li ho registrati specificamente in disordine, lontano dalla tentazione, per così dire ... quindi vengono risposte, il punto con la virgola è registrata.
0; 17/22; 3/4; 2/5; 1; 25.
E ora facciamo conclusioni. Se tutto è successo - sono contento per te! Calcoli elementari con frazioni - Non è il tuo problema! Puoi fare cose più serie. Altrimenti...
Quindi hai uno dei due problemi. O sia allo stesso tempo.) Mancanza di conoscenza e (o) disattenzione. Ma questo risolto I problemi.
Se ti piace questo sito ...
A proposito, ho un'altra coppia di siti interessanti per te.)
È possibile accedere a risolvere esempi e scoprire il tuo livello. Test con controllo immediato. Impara - Con interesse!)
Puoi conoscere le caratteristiche e i derivati.
Questo articolo considera le azioni sulle frazioni. Le regole di aggiunta, sottrazione, moltiplicazione, divisione o erezione delle frazioni della frazione A B sono formate e giustificate, dove A e B possono essere numeri, espressioni numeriche o espressioni con variabili. In conclusione, saranno presi in considerazione esempi di soluzioni con una descrizione dettagliata.
Yandex.rtb r-a-339285-1
Regole per l'esecuzione di azioni con frazioni numeriche della forma generale
Le frazioni numeriche della vista generale hanno un numeratore e un denominatore in cui sono disponibili numeri naturali o espressioni numeriche. Se consideriamo tali frazioni, come 3 5, 2, 8 4, 1 + 2 · 3 4 · (5 - 2), 3 4 + 7 8 2, 3 - 0, 8, 1 2 · 2, π 1 - 2 3 + π, 2 0, 5 LN 3, si può vedere che il numeratore e il denominatore non possono avere solo numeri, ma anche espressioni di vario piano.
Definizione 1.
Ci sono regole per cui è in corso un'azione con le frazioni ordinarie. È adatto per le frazioni della forma generale:
- Quando si sottraono le frazioni con gli stessi denominatori, solo i numeri sono piegati, e il denominatore rimane lo stesso, vale a dire: un D ± c \u003d A ± C D, i valori di A, C e D ≠ 0 sono alcuni numeri o espressioni numeriche.
- Quando si aggiungono o sottraendo frazioni con diversi denominatori, è necessario portare a uno comune, dopo di che è aggiunta o sottraendo le frazioni ottenute con gli stessi indicatori. Alfabeticamente sembra un B ± c \u003d A · p ± c · r s, dove i valori A, B ≠ 0, c, d ≠ 0, p ≠ 0, r ≠ 0, s ≠ 0 sono numeri validie b · p \u003d d · r \u003d s. Quando p \u003d d e r \u003d b, quindi a B ± c \u003d A · D ± c · d b · d.
- Con la moltiplicazione di frazioni, un'azione viene eseguita con numeri, dopo di che con i denominatori, quindi otteniamo un B · c d \u003d A · c B · d, dove A, B ≠ 0, c, d ≠ 0 funge da numeri validi.
- Quando si divide la frazione sulla frazione, il primo è moltiplicato per il secondo retromarcia, cioè produciamo di sostituzione con luoghi di numeratore e denominatore: A B: C D \u003d A B · D c.
Motivazione delle regole
DEFINIZIONE 2.Ci sono i seguenti momenti matematici per far affidamento quando si calcolava:
- tratto frazionario significa un segno di divisione;
- la divisione è considerata moltiplicando il suo valore posteriore;
- applicando le proprietà delle azioni con numeri validi;
- applicazione della proprietà principale delle frazioni e delle disuguaglianze numeriche.
Con il loro aiuto, puoi trasformare la forma:
a D ± C D \u003d A · D - 1 ± C · D - 1 \u003d A ± C · D-1 \u003d A ± C D; A B ± C d \u003d A · P B · P ± c · r d · r \u003d a · p s · p · p · p · p ± c · r s; ab · cd \u003d a · db · d · b · cb · d \u003d a · d · a · d - 1 · B · c · b · d - 1 \u003d \u003d a · d · b · c · b · d - 1 · B · D - 1 \u003d A · D · B · cb · d · B · d - 1 \u003d \u003d (A · c) · (B · d) - 1 \u003d A · CB · D
Esempi
Nel paragrafo precedente, è stato detto sull'azione con le frazioni. Dopo questo è necessario semplificare la frazione. In dettaglio, questo argomento è stato considerato nel punto di conversione della frazione.
Per cominciare, considera un esempio di aggiunta e sottrarre frazioni con lo stesso denominatore.
Esempio 1.
Le frazioni 8 2, 7 e 1 2, 7 sono state fornite, quindi il numeratore deve essere ripiegato secondo la regola e riscrivere il denominatore.
Decisione
Quindi otteniamo una frazione del modulo 8 + 1 2, 7. Dopo aver completato l'aggiunta, otteniamo una frazione del modulo 8 + 1 2, 7 \u003d 9 2, 7 \u003d 90 27 \u003d 3 1 3. Quindi, 8 2, 7 + 1 2, 7 \u003d 8 + 1 2, 7 \u003d 9 2, 7 \u003d 90 27 \u003d 3 1 3.
Risposta: 8 2 , 7 + 1 2 , 7 = 3 1 3
C'è un altro modo per risolvere. Per cominciare, la transizione verso la specie di frazione ordinaria, dopo di che siamo semplificati. Sembra questo:
8 2 , 7 + 1 2 , 7 = 80 27 + 10 27 = 90 27 = 3 1 3
ESEMPIO 2.
Decluderemo da 1 a 2 3 · log 2 3 · log 2 5 + 1 fractions del modulo 2 3 3 · log 2 3 · log 2 5 + 1.
Dal momento che vengono forniti uguali denominanti, significa che eseguiamo il calcolo della frazione con lo stesso denominatore. Ci capiamo
1 - 2 3 · log 2 3 · log 2 5 + 1 - 2 3 3 · log 2 3 · log 2 5 + 1 \u003d 1 - 2 - 2 3 3 · log 2 3 · log 2 5 + 1
Esistono esempi di frazioni calcolatrici con diversi denominatori. Un punto importante è portare a un denominatore comune. Senza questo, non saremo in grado di eseguire ulteriori passi con frazioni.
Il processo assomiglia a remoto portare a un denominatore comune. Cioè, la ricerca del più piccolo divisore generale è realizzato nel denominatore, dopo il quale vengono aggiunti i fattori mancanti per le frazioni.
Se le frazioni pieghevoli non hanno moltiplicatori comuni, possono essere il loro lavoro.
ESEMPIO 3.
Considera l'esempio dell'aggiunta di frazioni 2 3 5 + 1 e 1 2.
Decisione
In questo caso, il Denominatore generale esegue il lavoro del denominatore. Quindi otteniamo quel 2 · 3 5 + 1. Quindi, quando si impostano fattori aggiuntivi, abbiamo che la prima frazione è uguale a 2 e al secondo 3 5 + 1. Dopo aver moltiplicato la frazione viene data al modulo 4 2 · 3 5 + 1. Total Drive 1 2 avrà un modulo 3 5 + 1 2 · 3 5 + 1. Le espressioni frazionali risultanti si piegano e lo prendono
2 3 5 + 1 + 1 2 \u003d 2 · 2 2 · 3 5 + 1 + 1 · 3 5 + 1 2 · 3 5 + 1 \u003d 4 2 · 3 5 + 1 + 3 5 + 1 2 · 3 5 + 1 \u003d 4 + 3 5 + 1 2 · 3 5 + 1 \u003d 5 + 3 5 2 · 3 5 + 1
Risposta: 2 3 5 + 1 + 1 2 \u003d 5 + 3 5 2 · 3 5 + 1
Quando abbiamo a che fare con le frazioni della forma generale, allora il più piccolo denominatore generale di solito non ha importanza. Come denominatore, non è redditizia prendere il prodotto dei numeri. Per cominciare, verificare se c'è un numero che è inferiore al valore rispetto al loro lavoro.
ESEMPIO 4.
Considerare secondo esempio 1 6 · 2 1 5 e 1 4 · 2 3 5, quando il loro prodotto sarà uguale a 6 · 2 1 5 · 4 · 2 3 5 \u003d 24 · 2 4 5. Quindi prendiamo 12 · 2 3 5 come denominatore generale.
Considera esempi di moltiplicazioni di frazioni della forma generale.
ESEMPIO 5.
Per fare ciò, è necessario produrre moltiplicazione 2 + 1 6 e 2 · 5 3 · 2 + 1.
Decisione
La seguente regola, è necessario riscrivere e scrivere un prodotto di numeri sotto forma di un denominatore. Otteniamo che 2 + 1 6 · 2 · 5 3 · 2 + 1 2 + 1 · 2 · 5 6 · 3 · 2 + 1. Quando la frazione è moltiplicata, può essere ridotta per semplificarlo. Quindi 5 · 3 3 2 + 1: 10 9 3 \u003d 5 · 3 3 2 + 1 · 9 3 10.
L'utilizzo della regola di transizione si divide alla moltiplicazione allo shot back, otteniamo una frazione inversa. Per fare ciò, il numeratore e il denominatore stanno cambiando in luoghi. Considera sull'esempio:
5 · 3 3 2 + 1: 10 9 3 \u003d 5 · 3 3 2 + 1 · 9 3 10
Dopodiché, moltiplicazione e semplificare la frazione risultante. Se necessario, quindi sbarazzarsi di irrazionalità nel denominatore. Ci capiamo
5 · 3 3 2 + 1: 10 9 3 \u003d 5 · 3 3 · 9 3 10 · 2 + 1 \u003d 5 · 2 10 · 2 + 1 \u003d 3 2 · 2 + 1 \u003d \u003d 3 · 2 - 1 2 · 2 + 1 · 2 - 1 \u003d 3 · 2 - 1 2 · 2 2 - 1 2 \u003d 3 · 2 - 1 2
Risposta: 5 · 3 3 2 + 1: 10 9 3 \u003d 3 · 2 - 1 2
Questo articolo è applicabile quando il numero o l'espressione numerica possono essere rappresentati come frazione avente un denominatore pari a 1, quindi l'azione con una simile frazione è considerata oggetto separato. Ad esempio, espressione 1 6 · 7 4 - 1 · 3 Si può vedere che la radice di 3 può essere sostituita da un'altra espressione di 3 1. Quindi questa voce sembrerà una moltiplicazione di due frazioni del modulo 1 6 · 7 4 - 1 · 3 \u003d 1 6 · 7 4 - 1 · 3 1.
Esecuzione dell'azione con frazioni contenenti variabili
Le regole discusse nel primo articolo sono applicabili per l'azione con le frazioni contenenti variabili. Considera la regola di deduzione quando i denominatori sono gli stessi.
È necessario dimostrare che A, C e D (D non è uguale a zero) possono essere espressioni e l'uguaglianza A D ± C D \u003d A ± C D è uguale alla sua area dei valori consentiti.
È necessario prendere una serie di variabili dispari. Quindi A, C, D dovrebbe prendere valori appropriati di un 0, C 0 e D 0.. La sostituzione del modulo A D ± C D risulta nella differenza del modulo A 0 D 0 ± C 0 D 0, dove secondo la regola di aggiunta, otteniamo la formula del modulo A 0 ± C 0 D 0. Se sostituiamo l'espressione A ± C D, quindi otteniamo la stessa frazione del modulo A 0 ± C 0 D 0. Da qui concludiamo che il valore selezionato che soddisfa OTZ, un ± C D e A D ± C D è considerato uguale.
Con qualsiasi valore delle variabili, questa espressione sarà uguale, cioè, sono chiamate identicamente uguali. Quindi questa espressione è considerata comprovata l'uguaglianza della forma A D ± c \u003d A ± c d.
Esempi di aggiunta e sottrazione di frazioni con variabili
Quando ci sono gli stessi denominatori, devi solo piegarsi o detrarre i numeri. Tale frazione può essere semplificata. A volte devi lavorare con frazioni identiche uguali, ma a prima vista, è impercettibile, in quanto è necessario eseguire alcune trasformazioni. Ad esempio, x 2 3 · x 1 3 + 1 e x 1 3 + 1 2 o 1 2 · Sin 2 α e peccato A · Cos a. Molto spesso semplificando l'espressione di origine per vedere gli stessi denominatori.
ESEMPIO 6.
Calcola: 1) x 2 + 1 x + x - 2 - 5 - xx + x-2, 2) LG 2 x + 4 x · (LGX + 2) + 4 · LGXX · (LGX + 2), X - 1 X - 1 + XX + 1.
Decisione
- Per calcolare, è necessario sottrarre le frazioni che hanno gli stessi denominatori. Quindi otteniamo quello x 2 + 1 x + x-2 - 5 - x x + x-2 \u003d x 2 + 1 - 5 - x x + x-2. Successivamente, è possibile eseguire la divulgazione di parentesi con il sollevamento di termini simili. Otteniamo quella x 2 + 1 - 5 - x x + x - 2 \u003d x 2 + 1 - 5 + x x + x - 2 \u003d x 2 + x - 4 x + x - 2
- Dal momento che i denominatori sono gli stessi, rimane solo per piegare i numeri, lasciando il denominatore: LG 2 x + 4 x · (LGX + 2) + 4 · LGXX · (LGX + 2) \u003d LG 2 x + 4 + 4 x · (LGX + 2)
L'aggiunta è stata completata. Si può vedere che è possibile ridurre la frazione. Il suo numeratore può essere rotolato dalla somma della somma della somma, quindi otteniamo (L G x + 2) 2 dalle formule di moltiplicazione abbreviata. Quindi lo otteniamo
L G 2 x + 4 + 2 · L G x X · (L G x + 2) \u003d (L G x + 2) 2 x · (l G x + 2) \u003d L G x + 2 x - Le frazioni specificate del modulo x-1 x-1 + x x + 1 con diversi denominatori. Dopo la conversione, puoi andare in aggiunta.
Considera una soluzione a due vie.
Il primo metodo è che il denominatore della prima frazione è sottoposto a decomposizione dei moltiplicatori con l'aiuto dei quadrati e con la sua successiva riduzione. Otteniamo una frazione di tipo
x - 1 x - 1 \u003d X - 1 (X - 1) · x + 1 \u003d 1 x + 1
Quindi x - 1 x - 1 + x x + 1 \u003d 1 x + 1 + x x + 1 \u003d 1 + x x + 1.
In questo caso, è necessario sbarazzarsi di irrazionalità nel denominatore.
1 + x x + 1 \u003d 1 + x · x - 1 x + 1 · x - 1 \u003d x - 1 + x · x - x x - 1
Il secondo metodo consiste nel moltiplicare il numeratore e il denominatore della seconda frazione sull'espressione x-1. Pertanto, ci sbarazziamo di irrazionalità e andiamo all'aggiunta di frazioni in presenza dello stesso denominatore. Poi
x - 1 x - 1 + xx + 1 \u003d x - 1 x - 1 + x · x - 1 x + 1 · x - 1 \u003d x - 1 x - 1 + x · x - xx - 1 \u003d x - 1 + x · x - xx - 1
Risposta: 1) x 2 + 1 x + x - 2 - 5 - xx + x - 2 \u003d x 2 + x - 4 x + x-2, 2) LG 2 x + 4 x · (LGX + 2) + 4 · LGXX · (LGX + 2) \u003d LGX + 2 X, 3) X - 1 X - 1 + XX + 1 \u003d X - 1 + X · X - XX - 1.
Nel secondo esempio, hanno inevitabilmente il portare a un denominatore comune. Per fare ciò, semplificare la frazione. Per aggiungere o sottomesso, è sempre necessario cercare un denominatore comune, che sembra un prodotto dei denominatori con l'aggiunta di guasti aggiuntivi ai numeri.
Esempio 7.
Calcola i valori delle frazioni: 1) x 3 + 1 x 7 + 2 · 2, 2) x + 1 x · ln 2 (x + 1) · (2 \u200b\u200bx-4) - Sin XX 5 · ln (x + 1) · (2 \u200b\u200bx-4), 3) 1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x
Decisione
- Nessun calcolo complesso non richiede un denominatore, quindi è necessario scegliere il loro prodotto del modulo 3 · x 7 + 2 · 2, quindi alla prima frazione x 7 + 2 · 2 sono selezionati come fattore aggiuntivo e 3 al secondo . Quando moltiplicando, otteniamo la frazione del modulo x 3 + 1 x 7 + 2 · 2 \u003d x · x 7 + 2 · 2 3 · x 7 + 2 · 2 + 3 · 1 3 · x 7 + 2 · 2 \u003d x · x 7 + 2 · 2 + 3 3 · x 7 + 2 · 2 \u003d x · x 7 + 2 · 2 · x + 3 3 · x 7 + 2 · 2
- Si può vedere che i denominatori sono presentati sotto forma di un lavoro, il che significa inutile per ulteriori trasformazioni. Un denominatore comune sarà considerato un prodotto del modulo x 5 · ln 2 x + 1 · 2 x-4. Quindi x 4.
È un fattore aggiuntivo alla prima frazione e ln (x + 1)
al secondo. Dopo di che produciamo sottrazione e otteniamo questo:
X + 1 X · LN 2 (X + 1) · 2 x - 4 - SIN XX 5 · LN (X + 1) · 2 x - 4 \u003d x + 1 · x 4 x 5 · LN 2 (x + 1) · 2 x - 4 - Sin X · ln x + 1 x 5 · ln 2 (x + 1) · (2 \u200b\u200bx-4) \u003d x + 1 · x 4 - Sin x · ln (x + 1) x 5 · LN 2 (x + 1) · (2 \u200b\u200bx-4) \u003d x · x 4 + x 4 - Sin X · ln (x + 1) x 5 · ln 2 (x + 1) · (2 X - 4) - Questo esempio ha senso quando si lavora con i denominatori. È necessario applicare le formule di differenza di dimensioni e il quadrato della quantità, poiché sono loro che darà l'opportunità di andare all'espressione del modulo 1 cos x - x · cos x + x + 1 (cos x + x ) 2. Si può vedere che la frarata è data a un comune denominatore. Otteniamo quello cos x - x · cos x + x 2.
Dopo di che lo otteniamo
1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x \u003d \u003d 1 cos x - x · cos x + x + 1 cos x + x 2 \u003d \u003d cos x + x cos x - x · cos x + x 2 + cos x - x cos x - x · cos x + x 2 \u003d \u003d cos x + x + cos x - x cos x - x · cos x + x 2 \u003d 2 · cos x cos x - x · Cos x + x 2
Risposta:
1) x 3 + 1 x 7 + 2 · 2 \u003d x · x 7 + 2 · 2 · x + 3 3 · x 7 + 2 · 2, 2) x + 1 x · ln 2 (x + 1) · 2 X - 4 - SIN XX 5 · LN (x + 1) · 2 x - 4 \u003d \u003d x · x 4 + x 4 - Sin X · ln (x + 1) x 5 · ln 2 (x + 1) · ( 2 x - 4), 3) 1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x \u003d 2 · cos x cos x - x · cos x + x 2.
Esempi di moltiplicazione di frazioni con variabili
Quando si moltiplicano frazioni, il numeratore viene moltiplicato per il numeratore e il denominatore al denominatore. Quindi puoi applicare la proprietà dell'abbreviazione.
ESEMPIO 8.
Fai moltiplicazione di frazioni x + 2 · x x 2 · ln x 2 · ln x + 1 e 3 · x 2 1 3 · x + 1 - 2 peccato 2 · x - x.
Decisione
La moltiplicazione deve essere eseguita. Ci capiamo
x + 2 · xx 2 · ln x 2 · ln x + 1 · 3 · x 2 1 3 · x + 1 - 2 peccato (2 · x - x) \u003d x - 2 · x · 3 · x 2 1 3 · X + 1 - 2 x 2 · LN x 2 · ln x + 1 · Sin (2 · x - x)
Il numero 3 viene trasferito al primo posto per la comodità del conteggio, e puoi ridurre la frazione su x 2, quindi otteniamo l'espressione
3 · x - 2 · x · x 1 3 · x + 1 - 2 ln x 2 · ln x + 1 · peccato (2 · x - x)
Risposta: x + 2 · xx 2 · ln x 2 · ln x + 1 · 3 · x 2 1 3 · x + 1 - 2 peccato (2 · x - x) \u003d 3 · x - 2 · x · x 1 3 · x + 1 - 2 ln x 2 · ln x + 1 · peccato (2 · x - x).
Divisione
Divisione in frazioni è simile alla moltiplicazione, poiché la prima frazione è moltiplicata per la seconda inversione. Se prendiamo ad esempio la frazione x + 2 · xx 2 · ln x 2 · ln x + 1 e diviso per 3 · x 2 1 3 · x + 1 - 2 Sin 2 · x - x, quindi questo può essere scritto in un modo così come
x + 2 · xx 2 · ln x 2 · ln x + 1: 3 · x 2 1 3 · x + 1 - 2 peccato (2 · x-x), dopo di che è sostituito dal prodotto del modulo x + + 2 · xx 2 · ln x 2 · ln x + 1 · 3 · x 2 1 3 · x + 1 - 2 peccato (2 · x - x)
Erend in grado
Rivolviemo alla considerazione dell'azione con le frazioni del tipo generale con l'esercizio nel grado. Se c'è una laurea con una figura naturale, l'azione è considerata come moltiplicando le stesse frazioni. Ma si consiglia di utilizzare un approccio comune in base alle proprietà dei gradi. Qualsiasi espressione A e C, dove è identicamente uguale a zero, e qualsiasi valido r sull'OTZ per esprimere il modulo A C R è un'uguaglianza valida A C R \u003d A R C R. Il risultato è la frazione, eretta in una laurea. Ad esempio, considerare:
x 0, 7 - π · LN 3 x - 2 - 5 x + 1 2, 5 \u003d x 0, 7 - π · LN 3 x - 2 - 5 2, 5 x + 1 2, 5
Procedura per l'esecuzione di azioni con frazioni
Le azioni sulle frazioni vengono eseguite in base a determinate regole. In pratica, notiamo che l'espressione può contenere diverse frazioni o espressioni frazionali. Quindi è necessario eseguire tutte le azioni in un ordine rigoroso: sollevare il grado, moltiplicare, dividere, quindi piegare e sottrarre. Se ci sono parentesi, la prima azione viene eseguita in essi.
Esempio 9.
Calcola 1 - x cos X - 1 c o s x · 1 + 1 x.
Decisione
Dal momento che abbiamo lo stesso denominatore, quindi 1 - x cos x e 1 c o s x, ma è impossibile produrre sottrazione in base alla regola, le prime azioni vengono eseguite tra parentesi, dopo di quale moltiplicazione e quindi aggiunta. Quindi quando si calcola lo otteniamo
1 + 1 x \u003d 1 1 + 1 x \u003d x x + 1 x \u003d x + 1 x
Quando si sostituisce l'espressione nell'originale, otteniamo che 1 è x cos x - 1 cos x · x + 1 x. Quando moltiplicando fringa, abbiamo: 1 cos x · x + 1 x \u003d x + 1 cos x · x. Producendo tutte le sostituzioni, otteniamo 1 - x cos x - x + 1 cos x · x. Ora è necessario lavorare con frazioni che hanno diversi denominatori. Noi abbiamo:
x · 1 - x cos x · x - x + 1 cos x · x \u003d x · 1 - x - 1 + x cos x · x \u003d x - x - x - 1 cos x · x \u003d - x + 1 cos x · X.
Risposta: 1 - x cos X - 1 c o s x · 1 + 1 x \u003d - x + 1 cos x · x.
Se noti un errore nel testo, selezionalo e premi Ctrl + Invio
1º. Interi- Questi sono numeri utilizzati con il punteggio. L'insieme di tutti i numeri naturali denotan, I.e.n \u003d (1, 2, 3, ...).
Frazioneviene chiamato un numero costituito da diversi pezzi di unità. Frazione ordinariachiamato il numero di specie in cui il numero naturale n.mostra quante parti uguali sono divise da un'unità e un numero naturale m.mostra quante parti simili sono prese. Numeri m.e n.chiamato di conseguenza numeratoree denominatorefrazione.
Se il numeratore è inferiore al denominatore, viene chiamata la frazione ordinaria giusto; Se il numeratore è uguale al denominatore o più, allora la frazione è chiamata sbagliato. Il numero costituito dalle parti intere e frazionate è chiamato numero misto.
Per esempio,  - Le giuste frazioni ordinarie,
- Le giuste frazioni ordinarie,  - frazioni ordinarie errate, 1- numero misto.
- frazioni ordinarie errate, 1- numero misto.
2º. Durante l'esecuzione di azioni sulle frazioni ordinarie, dovrebbero essere ricordate le seguenti regole:
1) La proprietà principale del fraci. Se il numeratore e il denominatore della frazione vengono moltiplicati o suddivisi in uno e lo stesso numero naturale, quindi risulta la frazione uguale a questo.
Ad esempio, a)  ; b)
; b)  .
.
La divisione del numeratore e del denominatore della frazione sul loro divisore comune, diverso da una, è chiamata riduzione del fraci.
2) Per effettuare un numero misto da presentare sotto forma di una frazione errata, è necessario moltiplicare come una funzione della parte frazionata e aggiungere il numero di parte frazionario al prodotto risultante, scrivi la somma risultante della frazione e del il denominatore è lasciato per lo stesso.
Allo stesso modo, qualsiasi numero naturale può essere scritto come una frazione errata con qualsiasi denominatore.
Ad esempio, a)  , come
, come  ; b)
; b)  eccetera.
eccetera.
3) In modo che il colpo sbagliato sia scritto nella forma numero misto (cioè, dalla frazione sbagliata di allocare un'intera parte), un numeratore dovrebbe essere diviso in un denominatore, privato dalla divisione da prendere come parte intera, il residuo è come un numeratore, il denominatore è lasciato per lo stesso.
Ad esempio, a)  Dal 200: 7 \u003d 28 (OST 4); b)
Dal 200: 7 \u003d 28 (OST 4); b)  Dal 20: 5 \u003d 4 (OST 0).
Dal 20: 5 \u003d 4 (OST 0).
4) Per portare la frazione al minimo denominatore comune, è necessario trovare i più piccoli denominatori più comuni (NOC) di queste frazioni (sarà il loro minimo denominatore comune), dividere il minimo denominatore comune ai Denominatori dei dati delle frazioni (cioè, trova errori aggiuntivi per frazioni), moltiplicare il numeratore e il denominatore di ciascuna frazione sul suo fattore aggiuntivo.
Ad esempio, diamo le frazioni  al minimo denominatore generale:
al minimo denominatore generale:
 ,
, ,
, ;
;
630: 18 = 35, 630: 10 = 63, 630: 21 = 30.
Significa  ;
; ;
; .
.
5) Regole per l'azione aritmetica sulle normali frazioni:
(a) Aggiunta e sottrazione di frazioni con gli stessi denominatori viene eseguita secondo la regola:
 .
.
b) L'aggiunta e la sottrazione di frazioni con diversi denominatori viene eseguita in base alla regola), preindominando le frazioni al minimo denominatore generale.
c) Quando si aggiungono e sottraendo numeri misti, è possibile trasformarli in frazioni erratee quindi eseguire le regole delle regole) IB),
d) Quando si moltiplicano i frinati utilizzano la regola:
 .
.
e) Dividere una frazione a un'altra, è necessario moltiplicare il numero, il divisore inversa:
 .
.
f) Quando si moltiplicano e dividendo i numeri misti, sono pre-trasferiti a frazioni errate, e quindi godere delle regole) cioè).
3º. Quando si risolvono gli esempi su tutti i passaggi con le frazioni, è necessario ricordare che le prime azioni vengono eseguite tra parentesi. Sia tra parentesi che fuori per la prima volta eseguono la moltiplicazione e la divisione, quindi aggiunta e sottrazione.
Considera l'esecuzione delle norme di cui sopra sull'esempio.
Esempio 1. Calcola:  .
.
1)  ;
;
2)  ;
;
5)  . Risposta: 3.
. Risposta: 3.