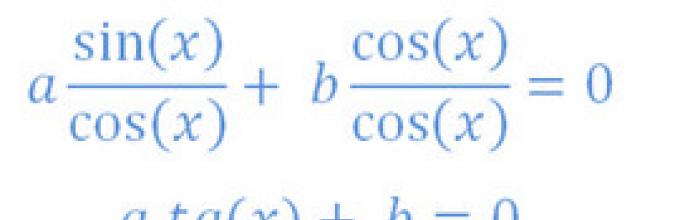Μάθημα και παρουσίαση με θέμα: "Επίλυση απλών τριγωνομετρικών εξισώσεων"
Πρόσθετα υλικά
Αγαπητοί χρήστες, μην ξεχάσετε να αφήσετε τα σχόλια, τις κριτικές, τις επιθυμίες σας! Όλα τα υλικά έχουν ελεγχθεί από ένα πρόγραμμα προστασίας από ιούς.
Εγχειρίδια και προσομοιωτές στο ηλεκτρονικό κατάστημα Integral για τον βαθμό 10 από 1C
Επίλυση προβλημάτων στη γεωμετρία. Διαδραστικές εργασίες για οικοδόμηση στο χώρο
Περιβάλλον λογισμικού "1C: Mathematical Constructor 6.1"
Τι θα μελετήσουμε:
1. Τι είναι οι τριγωνομετρικές εξισώσεις;
3. Δύο κύριες μέθοδοι λύσης τριγωνομετρικές εξισώσεις.
4. Ομοιογενείς τριγωνομετρικές εξισώσεις.
5. Παραδείγματα.
Τι είναι οι τριγωνομετρικές εξισώσεις;
Παιδιά, έχουμε ήδη μελετήσει arcsine, arccosine, arctangent και arccotangent. Ας δούμε τώρα τις τριγωνομετρικές εξισώσεις γενικά.
Οι τριγωνομετρικές εξισώσεις είναι εξισώσεις στις οποίες μια μεταβλητή περιέχεται κάτω από το πρόσημο μιας τριγωνομετρικής συνάρτησης.
Ας επαναλάβουμε τη μορφή επίλυσης των απλούστερων τριγωνομετρικών εξισώσεων:
1)Αν |a|≤ 1, τότε η εξίσωση cos(x) = a έχει λύση:
X= ± arccos(a) + 2πk
2) Αν |a|≤ 1, τότε η εξίσωση sin(x) = a έχει λύση:
3) Αν |a| > 1, τότε η εξίσωση sin(x) = a και cos(x) = a δεν έχουν λύσεις 4) Η εξίσωση tg(x)=a έχει λύση: x=arctg(a)+ πk
5) Η εξίσωση ctg(x)=a έχει λύση: x=arcctg(a)+ πk
Για όλους τους τύπους το k είναι ακέραιος
Οι απλούστερες τριγωνομετρικές εξισώσεις έχουν τη μορφή: T(kx+m)=a, T είναι κάποια τριγωνομετρική συνάρτηση.
Παράδειγμα.Λύστε τις εξισώσεις: α) sin(3x)= √3/2
Λύση:
Α) Ας συμβολίσουμε 3x=t και μετά θα ξαναγράψουμε την εξίσωσή μας με τη μορφή:
Η λύση αυτής της εξίσωσης θα είναι: t=((-1)^n)arcsin(√3 /2)+ πn.
Από τον πίνακα τιμών παίρνουμε: t=((-1)^n)×π/3+ πn.
Ας επιστρέψουμε στη μεταβλητή μας: 3x =((-1)^n)×π/3+ πn,
Τότε x= ((-1)^n)×π/9+ πn/3
Απάντηση: x= ((-1)^n)×π/9+ πn/3, όπου n είναι ακέραιος. (-1)^n – μείον ένα στη δύναμη του n.
Περισσότερα παραδείγματα τριγωνομετρικών εξισώσεων.
Λύστε τις εξισώσεις: α) cos(x/5)=1 b)tg(3x- π/3)= √3Λύση:
Α) Αυτή τη φορά ας προχωρήσουμε απευθείας στον υπολογισμό των ριζών της εξίσωσης:
X/5= ± arccos(1) + 2πk. Τότε x/5= πk => x=5πk
Απάντηση: x=5πk, όπου k είναι ακέραιος.
Β) Το γράφουμε με τη μορφή: 3x- π/3=arctg(√3)+ πk. Γνωρίζουμε ότι: arctan(√3)= π/3
3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3
Απάντηση: x=2π/9 + πk/3, όπου k είναι ακέραιος.
Λύστε τις εξισώσεις: cos(4x)= √2/2. Και βρείτε όλες τις ρίζες στο τμήμα.
Λύση:
Ας λύσουμε την εξίσωσή μας σε γενική μορφή: 4x= ± arccos(√2/2) + 2πk
4x= ± π/4 + 2πk;
X= ± π/16+ πk/2;
Τώρα ας δούμε ποιες ρίζες πέφτουν στο τμήμα μας. Στο k Στο k=0, x= π/16, είμαστε μέσα δεδομένο τμήμα.
Με k=1, x= π/16+ π/2=9π/16, ξαναχτυπάμε.
Για k=2, x= π/16+ π=17π/16, αλλά εδώ δεν χτυπήσαμε, που σημαίνει ότι για μεγάλο k επίσης προφανώς δεν θα χτυπήσουμε.
Απάντηση: x= π/16, x= 9π/16
Δύο βασικές μέθοδοι λύσης.
Εξετάσαμε τις απλούστερες τριγωνομετρικές εξισώσεις, αλλά υπάρχουν και πιο σύνθετες. Για την επίλυσή τους χρησιμοποιείται η μέθοδος εισαγωγής νέας μεταβλητής και η μέθοδος παραγοντοποίησης. Ας δούμε παραδείγματα.Ας λύσουμε την εξίσωση:
Λύση:
Για να λύσουμε την εξίσωσή μας, θα χρησιμοποιήσουμε τη μέθοδο εισαγωγής μιας νέας μεταβλητής, που δηλώνει: t=tg(x).
Ως αποτέλεσμα της αντικατάστασης παίρνουμε: t 2 + 2t -1 = 0
Ας βρούμε τις ρίζες της δευτεροβάθμιας εξίσωσης: t=-1 και t=1/3
Τότε tg(x)=-1 και tg(x)=1/3, παίρνουμε την απλούστερη τριγωνομετρική εξίσωση, ας βρούμε τις ρίζες της.
X=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk.
Απάντηση: x= -π/4+πk; x=arctg(1/3) + πk.
Παράδειγμα επίλυσης εξίσωσης
Λύστε εξισώσεις: 2sin 2 (x) + 3 cos(x) = 0
Λύση:
Ας χρησιμοποιήσουμε την ταυτότητα: sin 2 (x) + cos 2 (x)=1
Η εξίσωσή μας θα έχει τη μορφή: 2-2cos 2 (x) + 3 cos (x) = 0
2 cos 2 (x) - 3 cos(x) -2 = 0
Ας εισαγάγουμε την αντικατάσταση t=cos(x): 2t 2 -3t - 2 = 0
Η λύση της τετραγωνικής μας εξίσωσης είναι οι ρίζες: t=2 και t=-1/2
Τότε cos(x)=2 και cos(x)=-1/2.
Επειδή Το συνημίτονο δεν μπορεί να πάρει τιμές μεγαλύτερες από ένα, τότε το cos(x)=2 δεν έχει ρίζες.
Για cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk
Απάντηση: x= ±2π/3 + 2πk
Ομοιογενείς τριγωνομετρικές εξισώσεις.
Ορισμός: Οι εξισώσεις της μορφής a sin(x)+b cos(x) ονομάζονται ομοιογενείς τριγωνομετρικές εξισώσεις πρώτου βαθμού.Εξισώσεις της φόρμας
ομοιογενείς τριγωνομετρικές εξισώσεις δεύτερου βαθμού.
Για να λύσετε μια ομοιογενή τριγωνομετρική εξίσωση πρώτου βαθμού, διαιρέστε την με το cos(x):  Δεν μπορείτε να διαιρέσετε με το συνημίτονο αν είναι ίσο με μηδέν, ας βεβαιωθούμε ότι δεν ισχύει αυτό:
Δεν μπορείτε να διαιρέσετε με το συνημίτονο αν είναι ίσο με μηδέν, ας βεβαιωθούμε ότι δεν ισχύει αυτό:
Έστω cos(x)=0, τότε asin(x)+0=0 => sin(x)=0, αλλά το ημίτονο και το συνημίτονο δεν είναι ίσα με μηδέν ταυτόχρονα, παίρνουμε μια αντίφαση, ώστε να μπορούμε να διαιρέσουμε με ασφάλεια κατά μηδέν.
Λύστε την εξίσωση:
Παράδειγμα: cos 2 (x) + sin(x) cos(x) = 0
Λύση:
Ας βγάλουμε τον κοινό παράγοντα: cos(x)(c0s(x) + sin (x)) = 0
Τότε πρέπει να λύσουμε δύο εξισώσεις:
Cos(x)=0 και cos(x)+sin(x)=0
Cos(x)=0 στο x= π/2 + πk;
Θεωρήστε την εξίσωση cos(x)+sin(x)=0 Διαιρέστε την εξίσωσή μας με cos(x):
1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk
Απάντηση: x= π/2 + πk και x= -π/4+πk
Πώς να λύσετε ομοιογενείς τριγωνομετρικές εξισώσεις δεύτερου βαθμού;
Παιδιά, να ακολουθείτε πάντα αυτούς τους κανόνες!
1. Δείτε με τι ισούται ο συντελεστής a, αν a=0 τότε η εξίσωσή μας θα πάρει τη μορφή cos(x)(bsin(x)+ccos(x)), ένα παράδειγμα της λύσης της οποίας βρίσκεται στην προηγούμενη διαφάνεια
2. Εάν a≠0, τότε πρέπει να διαιρέσετε και τις δύο πλευρές της εξίσωσης με το συνημίτονο στο τετράγωνο, παίρνουμε:

Αλλάζουμε τη μεταβλητή t=tg(x) και παίρνουμε την εξίσωση:
Λύστε το παράδειγμα αρ.:3
Λύστε την εξίσωση:Λύση:
Ας διαιρέσουμε και τις δύο πλευρές της εξίσωσης με το συνημίτονο: 
Αλλάζουμε τη μεταβλητή t=tg(x): t 2 + 2 t - 3 = 0
Ας βρούμε τις ρίζες της δευτεροβάθμιας εξίσωσης: t=-3 και t=1
Τότε: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk
Tg(x)=1 => x= π/4+ πk
Απάντηση: x=-arctg(3) + πk και x= π/4+ πk
Λύστε το παράδειγμα αρ.:4
Λύστε την εξίσωση:Λύση:
Ας μεταμορφώσουμε την έκφρασή μας:

Μπορούμε να λύσουμε τέτοιες εξισώσεις: x= - π/4 + 2πk και x=5π/4 + 2πk
Απάντηση: x= - π/4 + 2πk και x=5π/4 + 2πk
Λύστε το παράδειγμα αρ.:5
Λύστε την εξίσωση:Λύση:
Ας μεταμορφώσουμε την έκφρασή μας:

Ας εισαγάγουμε την αντικατάσταση tg(2x)=t:2 2 - 5t + 2 = 0
Η λύση της τετραγωνικής μας εξίσωσης θα είναι οι ρίζες: t=-2 και t=1/2
Τότε παίρνουμε: tg(2x)=-2 και tg(2x)=1/2
2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/2
2x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2
Απάντηση: x=-arctg(2)/2 + πk/2 και x=arctg(1/2)/2+ πk/2
Προβλήματα για ανεξάρτητη λύση.
1) Λύστε την εξίσωσηΑ) sin(7x)= 1/2 β) cos(3x)= √3/2 γ) cos(-x) = -1 δ) tg(4x) = √3 δ) ctg(0.5x) = -1.7
2) Λύστε τις εξισώσεις: sin(3x)= √3/2. Και βρείτε όλες τις ρίζες στο τμήμα [π/2; π].
3) Λύστε την εξίσωση: κούνια 2 (x) + 2 κούνια (x) + 1 =0
4) Λύστε την εξίσωση: 3 sin 2 (x) + √3sin (x) cos(x) = 0
5) Λύστε την εξίσωση: 3sin 2 (3x) + 10 sin(3x)cos(3x) + 3 cos 2 (3x) =0
6) Λύστε την εξίσωση: cos 2 (2x) -1 - cos(x) =√3/2 -sin 2 (2x)
Οι κύριες μέθοδοι για την επίλυση τριγωνομετρικών εξισώσεων είναι: η αναγωγή των εξισώσεων στην απλούστερη (χρησιμοποιώντας τριγωνομετρικούς τύπους), η εισαγωγή νέων μεταβλητών και η παραγοντοποίηση. Ας δούμε τη χρήση τους με παραδείγματα. Προσοχή στη μορφή γραφής λύσεων τριγωνομετρικών εξισώσεων.
Απαραίτητη προϋπόθεση για την επιτυχή επίλυση τριγωνομετρικών εξισώσεων είναι η γνώση τριγωνομετρικών τύπων (θέμα 13 της εργασίας 6).
Παραδείγματα.
1. Εξισώσεις ανάγονται στην απλούστερη.
1) Λύστε την εξίσωση
Λύση:
Απάντηση:
2) Να βρείτε τις ρίζες της εξίσωσης
(sinx + cosx) 2 = 1 – sinxcosx, που ανήκουν στο τμήμα.
Λύση:
Απάντηση:
2. Εξισώσεις που ανάγονται σε τετραγωνικό.
1) Λύστε την εξίσωση 2 sin 2 x – cosx –1 = 0.
Λύση:Χρησιμοποιώντας αμαρτία τύπος 2 x = 1 – cos 2 x, παίρνουμε
Απάντηση:
2) Λύστε την εξίσωση cos 2x = 1 + 4 cosx.
Λύση:Χρησιμοποιώντας τον τύπο cos 2x = 2 cos 2 x – 1, παίρνουμε
Απάντηση:
3) Λύστε την εξίσωση tgx – 2ctgx + 1 = 0
Λύση:
Απάντηση:
3. Ομογενείς εξισώσεις
1) Λύστε την εξίσωση 2sinx – 3cosx = 0
Λύση: Έστω cosx = 0, μετά 2sinx = 0 και sinx = 0 – αντίφαση με το γεγονός ότι sin 2 x + cos 2 x = 1. Αυτό σημαίνει cosx ≠ 0 και μπορούμε να διαιρέσουμε την εξίσωση με cosx. Παίρνουμε
Απάντηση:
2) Λύστε την εξίσωση 1 + 7 cos 2 x = 3 sin 2x
Λύση:
Χρησιμοποιούμε τους τύπους 1 = sin 2 x + cos 2 x και sin 2x = 2 sinxcosx, παίρνουμε
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Έστω cosx = 0, τότε sin 2 x = 0 και sinx = 0 – αντίφαση με το γεγονός ότι sin 2 x + cos 2 x = 1.
Αυτό σημαίνει cosx ≠ 0 και μπορούμε να διαιρέσουμε την εξίσωση με cos 2 x .
Παίρνουμε
tg 2 x – 6 tgx + 8 = 0
Ας συμβολίσουμε tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y2 = 2
α) tgx = 4, x= arctan4 + 2 κ, κ
β) tgx = 2, x= arctan2 + 2 κ, κ .
Απάντηση: arctg4 + 2 κ, arctan2 + 2 κ,κ
4. Εξισώσεις της μορφής ένα sinx + σι cosx = s, s≠ 0.
1) Λύστε την εξίσωση.
Λύση:
Απάντηση:
5. Εξισώσεις που λύνονται με παραγοντοποίηση.
1) Λύστε την εξίσωση sin2x – sinx = 0.
Ρίζα της εξίσωσης φά (Χ) = φ ( Χ) μπορεί να χρησιμεύσει μόνο ως ο αριθμός 0. Ας ελέγξουμε αυτό:
cos 0 = 0 + 1 – η ισότητα είναι αληθής.
Ο αριθμός 0 είναι η μόνη ρίζα αυτής της εξίσωσης.
Απάντηση: 0.
Θέμα μαθήματος:Τριγωνομετρικές εξισώσεις αναγώγιμες σε τετραγωνικές, ομοιογενείς τριγωνομετρικές εξισώσεις.
Τύπος μαθήματος: Συνδυαστικό μάθημα.
Στόχοι μαθήματος:
- Εισαγάγετε την έννοια των ομοιογενών τριγωνομετρικών εξισώσεων που μπορούν να αναχθούν σε τετραγωνικές εξισώσεις.
- Εισάγετε την έννοια των τριγωνομετρικών εξισώσεων 1ου και 2ου βαθμού.
- Να αναπτύξουν στους μαθητές την ικανότητα να λύνουν τις εξεταζόμενες εξισώσεις σε βασικό επίπεδο.
- Να αναπτύξουν την ικανότητα ανάλυσης και εξαγωγής συμπερασμάτων.
- Αναπτύξτε τις δεξιότητες αυτοανάλυσης και ελέγχου.
- Καλλιεργήστε το αίσθημα ευθύνης.
- Αναπτύξτε δεξιότητες για εργασία σε ομάδα.
- Εξοπλισμός μαθήματος: αφίσες, κάρτες, αυτοαξιολογήσεις, ένα σετ καρτών για ανεξάρτητη εργασία, κάρτες σημάτων.
Δομή μαθήματος:
1. Οργανωτικό στάδιο.
2. Στάδιο ελέγχου της εργασίας.
3. Το στάδιο προετοιμασίας των μαθητών για ενεργητική και συνειδητή αφομοίωση νέου υλικού. Εισαγωγή στο θέμα του μαθήματος. Θέτοντας στόχους και στόχους.
4. Στάδιο αφομοίωσης νέας γνώσης.
5. Το στάδιο ελέγχου της κατανόησης του νέου υλικού από τους μαθητές.
6. Στάδιο ενοποίησης νέου υλικού.
7. Στάδιο ενημέρωσης των μαθητών για την εργασία.
8. Στάδιο ολοκληρωμένου ελέγχου γνώσεων.
9. Συνοψίζοντας. Αντανάκλαση.
1. Οργανωτικό στάδιο .
- προετοιμάζει τους μαθητές για εργασία στην τάξη.
2. Στάδιο ελέγχου της εργασίας .
- διαπιστώνουν την παρουσία και την ορθότητα των εργασιών για το σπίτι από όλους τους μαθητές.
3. Το στάδιο προετοιμασίας των μαθητών για ενεργητική και συνειδητή αφομοίωση νέου υλικού.
- δημιουργώντας μια προβληματική κατάσταση, οδηγήστε τους μαθητές σε νέους τύπους τριγωνομετρικών εξισώσεων. Ο δάσκαλος εφιστά την προσοχή των μαθητών στον μαγνητικό πίνακα, όπου βρίσκονται κάρτες με πολλές τριγωνομετρικές εξισώσεις και τους ζητά να υποδείξουν πώς να τις λύσουν.
1) cos (4x-2)=2
3) cos 2 x-2cosx=0
5) 8 αμαρτία 2 x-6 αμαρτία x-5=0
6)8 συν 2 2χ+6 αμαρτία 2χ-3=0
7)2sin x- 3 cos x=0
9)3 sin 2 x- 4sin x cos x +cos 2 x=0
Οι μαθητές κοιτάζουν προσεκτικά τον μαγνητικό πίνακα και εξηγούν πώς να λύσουν αυτή ή εκείνη την εξίσωση. Εάν ο δάσκαλος δεν έχει σχόλια, η κάρτα με την παραπάνω εξίσωση αφαιρείται από τον μαγνητικό πίνακα.
Ως αποτέλεσμα της δουλειάς που έγινε, οι εξισώσεις παρέμειναν στον μαγνητικό πίνακα, οι μαθητές δεν μπορούσαν να βρουν τρόπο να τις λύσουν. (Νο. 5, 7)
4. Στάδιο αφομοίωσης νέας γνώσης.
Εισαγάγετε την έννοια των «Τριγωνομετρικών εξισώσεων αναγώγιμων σε τετραγωνικές».
- εισαγάγετε την έννοια των «τριγωνομετρικών εξισώσεων αναγωγούμενων σε τετραγωνικές»·
- εισαγάγετε την έννοια των ομοιογενών τριγωνομετρικών εξισώσεων.
- ανάλυση μεθόδων για την επίλυση ομοιογενών τριγωνομετρικών εξισώσεων 1ου και 2ου βαθμού.
- επιτύχει την ικανότητα προσδιορισμού της μορφής ομοιογενών τριγωνομετρικών εξισώσεων.
- κατακτήστε τις γενικές τεχνικές για την επίλυση τριγωνομετρικών εξισώσεων που μπορούν να αναχθούν σε τετραγωνικές και ομοιογενείς τριγωνομετρικές εξισώσεις.
Ο δάσκαλος ονομάζει τους τύπους των υπόλοιπων εξισώσεων και καλεί τους μαθητές να γράψουν το θέμα του μαθήματος «Τριγωνομετρικές εξισώσεις που λύνονται με αναγωγή σε τετραγωνικές. Ομογενείς τριγωνομετρικές εξισώσεις 1ου και 2ου βαθμού."
Ο δάσκαλος κάνει σημειώσεις στον πίνακα και οι μαθητές γράφουν στο τετράδιό τους:
Τριγωνομετρικές εξισώσεις που λύνονται με αναγωγή σε τετραγωνικές εξισώσεις.
1) Οι εξισώσεις της μορφής A×sin2 t +B×sin t + C = 0, όπου A 1 0, λύνονται με αναγωγή σε τετραγωνικό με αντικατάσταση sin t = y (οι εξισώσεις με cos t, tg t, σtg t είναι λυθεί παρομοίως).
2) Εξισώσεις της μορφής A×sin2 t +B×cos t + C = 0. Κατά την επίλυση, η βασική τριγωνομετρική ταυτότητα sin2 t = 1 - cos2 t.
3) αμαρτία 2 t = a, a= . 4) cos 2 t = a, a= .
5) tg 2 t = a, a= . 6) κούνια 2 t = a, a=
Αναλύεται λεπτομερώς η λύση της εξίσωσης Νο. 5, 4. Η λύση της εξίσωσης Νο. 6 πραγματοποιείται με την ενεργό συμμετοχή της τάξης. Για την επίλυση της εξίσωσης Νο. 8 καλείται ένας μαθητής (προαιρετικό).
Ομοιογενείς τριγωνομετρικές εξισώσεις 1ου και 2ου βαθμού.
Μια εξίσωση στην οποία κάθε όρος έχει τον ίδιο βαθμό ονομάζεται ομοιογενής.
1) Οι εξισώσεις της μορφής A×sin t +B×cos t = 0, όπου A 1 0, B 1 0, ονομάζονται ομοιογενείς τριγωνομετρικές εξισώσεις βαθμού 1. Επιλύονται διαιρώντας και τις δύο πλευρές με το κόστος t ¹ 0. Έχουμε A× tg t + B = 0.
2) Οι εξισώσεις της μορφής A×sin2 t +B sin t×cos t + С×cos2 t = 0 ονομάζονται ομοιογενείς τριγωνομετρικές εξισώσεις βαθμού 2. Επιλύονται διαιρώντας και τις δύο πλευρές με cos2 t ¹ 0. Έχουμε A× tg2 t + B× tg t + C = 0.
Ο δάσκαλος λύνει την εξίσωση Νο 7, με αναλυτική εξήγηση. Κατά την επίλυση της εξίσωσης Νο. 9, χρησιμοποιώντας ερωτήσεις, συνδέει τους μαθητές με ενεργή εργασία. Αφού μειώσει την εξίσωση στη μορφή 3tg2 t - 4 tg t + 1 = 0, καλεί τους μαθητές να πάνε στον πίνακα εάν το επιθυμούν και να λύσουν την εξίσωση που προκύπτει.
- Το στάδιο ελέγχου της κατανόησης του νέου υλικού από τους μαθητές.
Εργο: προσδιορίστε εάν οι μαθητές έχουν μάθει πώς να λύνουν έναν νέο τύπο εξισώσεων.
SFZ ( ανεξάρτητη εργασίαγια το σχηματισμό γνώσης).
Προσδιορίστε τον τύπο της εξίσωσης και υποδείξτε πώς να την λύσετε.
2)5 αμαρτία 3x+4cos3x=0 ;
3) sin 2 x+14sinx*cosx-15cos 2 x=0;
4) 1 + 7cos2 x + 3sin2 x = 0;
5)sin2x+sin 2 x=0 .
6. Στάδιο ενοποίησης νέου υλικού.
Εργο: εμπεδώνουν στους μαθητές τις γνώσεις και τις δεξιότητες που έλαβαν στο μάθημα.
Ο δάσκαλος ζητά από τους μαθητές να λύσουν τις παρακάτω εξισώσεις στον πίνακα:
7. Στάδιο ενημέρωσης των μαθητών για την εργασία.
Στόχοι: ενημέρωση των μαθητών εργασία για το σπίτι, δώστε σύντομες οδηγίες για την εφαρμογή του.
- Ελέγξτε τις σημειώσεις στο σημειωματάριό σας.
- αναλύστε τη λύση των παραδειγμάτων Νο 1 - 6 από το σχολικό βιβλίο, σελ. 78 - 79.
- πλήρης αρ. 167a), β); Νο. 168 b); Νο. 169a); Νο. 170v).
- Οι δυνατοί μαθητές, αντί για το Νο 167, 168, μπορούν να λύσουν την εξίσωση:
15*(sin 2 x+sin x+ cos 2 2x) 2 +17+31sinx
8. Στάδιο ολοκληρωμένου ελέγχου γνώσεων.
Στόχοι: διεξοδική εξέταση των γνώσεων των μαθητών κατά την επίλυση εξισώσεων παρόμοιων με αυτές που συζητήθηκαν στο μάθημα, ανάπτυξη δεξιοτήτων αυτοανάλυσης και ελέγχου.
SFN (ανεξάρτητη εργασία για την ανάπτυξη δεξιοτήτων).
Λύστε τις εξισώσεις.
Επιλογή 1.
Επιλογή 2
Επιλογή 3
Επιλογή 4
9. Συνοψίζοντας. Αντανάκλαση.
Κατά την επίλυση πολλών μαθηματικά προβλήματα , ειδικά αυτές που συμβαίνουν πριν από τον βαθμό 10, η σειρά των ενεργειών που εκτελούνται που θα οδηγήσουν στον στόχο είναι σαφώς καθορισμένη. Τέτοια προβλήματα περιλαμβάνουν, για παράδειγμα, γραμμικές και τετραγωνικές εξισώσεις, γραμμικές και τετραγωνικές ανισότητες, κλασματικές εξισώσεις και εξισώσεις που ανάγονται σε τετραγωνικό. Η αρχή της επιτυχούς επίλυσης καθενός από τα αναφερόμενα προβλήματα είναι η εξής: είναι απαραίτητο να καθοριστεί ποιος τύπος προβλήματος επιλύεται, να θυμάστε την απαραίτητη σειρά ενεργειών που θα οδηγήσουν σε το επιθυμητό αποτέλεσμα, δηλ. απαντήστε και ακολουθήστε αυτά τα βήματα.
Είναι προφανές ότι η επιτυχία ή η αποτυχία στην επίλυση ενός συγκεκριμένου προβλήματος εξαρτάται κυρίως από το πόσο σωστά καθορίζεται ο τύπος της εξίσωσης που επιλύεται, πόσο σωστά αναπαράγεται η ακολουθία όλων των σταδίων της επίλυσής της. Φυσικά, είναι απαραίτητο να έχετε τις δεξιότητες για να εκτελέσετε μετασχηματισμοί ταυτότηταςκαι υπολογιστών.
Η κατάσταση είναι διαφορετική με τριγωνομετρικές εξισώσεις.Δεν είναι καθόλου δύσκολο να τεκμηριωθεί το γεγονός ότι η εξίσωση είναι τριγωνομετρική. Προκύπτουν δυσκολίες κατά τον καθορισμό της αλληλουχίας των ενεργειών που θα οδηγούσαν στη σωστή απάντηση.
Με εμφάνισηεξίσωση, μερικές φορές είναι δύσκολο να προσδιοριστεί ο τύπος του. Και χωρίς να γνωρίζουμε τον τύπο της εξίσωσης, είναι σχεδόν αδύνατο να επιλέξετε το σωστό από πολλές δεκάδες τριγωνομετρικούς τύπους.
Για να λύσετε μια τριγωνομετρική εξίσωση, πρέπει να δοκιμάσετε:
1. Φέρτε όλες τις συναρτήσεις που περιλαμβάνονται στην εξίσωση στις «ίδιες γωνίες».
2. Φέρτε την εξίσωση σε «πανομοιότυπες συναρτήσεις».
3. παραμετροποιήστε την αριστερή πλευρά της εξίσωσης κ.λπ.
Ας σκεφτούμε βασικές μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων.
I. Αναγωγή στις απλούστερες τριγωνομετρικές εξισώσεις
Διάγραμμα λύσης
Βήμα 1.Να εκφράσετε μια τριγωνομετρική συνάρτηση ως προς γνωστές συνιστώσες.
Βήμα 2.Βρείτε το όρισμα συνάρτησης χρησιμοποιώντας τους τύπους:
cos x = a; x = ±arccos a + 2πn, n ЄZ.
sin x = a; x = (-1) n arcsin a + πn, n Є Z.
tan x = a; x = αρκτάνη a + πn, n Є Z.
ctg x = a; x = arcctg a + πn, n Є Z.
Βήμα 3.Βρείτε την άγνωστη μεταβλητή.
Παράδειγμα.
2 cos(3x – π/4) = -√2.
Λύση.
1) cos(3x – π/4) = -√2/2.
2) 3x – π/4 = ±(π – π/4) + 2πn, n Є Z;
3x – π/4 = ±3π/4 + 2πn, n Є Z.
3) 3x = ±3π/4 + π/4 + 2πn, n Є Z;
x = ±3π/12 + π/12 + 2πn/3, n Є Z;
x = ±π/4 + π/12 + 2πn/3, n Є Z.
Απάντηση: ±π/4 + π/12 + 2πn/3, n Є Z.
II. Αντικατάσταση μεταβλητής
Διάγραμμα λύσης
Βήμα 1.Να μειώσετε την εξίσωση σε αλγεβρική μορφή σε σχέση με μία από τις τριγωνομετρικές συναρτήσεις.
Βήμα 2.Σημειώστε τη συνάρτηση που προκύπτει με τη μεταβλητή t (αν χρειάζεται, εισάγετε περιορισμούς στο t).
Βήμα 3.Καταγράψτε και λύστε την αλγεβρική εξίσωση που προκύπτει.
Βήμα 4.Κάντε μια αντίστροφη αντικατάσταση.
Βήμα 5.Να λύσετε την απλούστερη τριγωνομετρική εξίσωση.
Παράδειγμα.
2cos 2 (x/2) – 5sin (x/2) – 5 = 0.
Λύση.
1) 2(1 – sin 2 (x/2)) – 5sin (x/2) – 5 = 0;
2sin 2 (x/2) + 5sin (x/2) + 3 = 0.
2) Έστω sin (x/2) = t, όπου |t| ≤ 1.
3) 2t 2 + 5t + 3 = 0;
t = 1 ή e = -3/2, δεν ικανοποιεί τη συνθήκη |t| ≤ 1.
4) sin(x/2) = 1.
5) x/2 = π/2 + 2πn, n Є Z;
x = π + 4πn, n Є Z.
Απάντηση: x = π + 4πn, n Є Z.
III. Μέθοδος μείωσης σειράς εξίσωσης
Διάγραμμα λύσης
Βήμα 1.Αντικαταστήστε αυτήν την εξίσωση με μια γραμμική, χρησιμοποιώντας τον τύπο για τη μείωση του βαθμού:
αμαρτία 2 x = 1/2 · (1 – cos 2x);
cos 2 x = 1/2 · (1 + cos 2x);
tg 2 x = (1 – cos 2x) / (1 + cos 2x).
Βήμα 2.Λύστε την εξίσωση που προκύπτει χρησιμοποιώντας τις μεθόδους I και II.
Παράδειγμα.
cos 2x + cos 2 x = 5/4.
Λύση.
1) cos 2x + 1/2 · (1 + cos 2x) = 5/4.
2) cos 2x + 1/2 + 1/2 · cos 2x = 5/4;
3/2 cos 2x = 3/4;
2x = ±π/3 + 2πn, n Є Z;
x = ±π/6 + πn, n Є Z.
Απάντηση: x = ±π/6 + πn, n Є Z.
IV. Ομογενείς εξισώσεις
Διάγραμμα λύσης
Βήμα 1.Μειώστε αυτήν την εξίσωση στη φόρμα
α) a sin x + b cos x = 0 (ομογενής εξίσωση πρώτου βαθμού)
ή στη θέα
β) a sin 2 x + b sin x · cos x + c cos 2 x = 0 (ομοιογενής εξίσωση δεύτερου βαθμού).
Βήμα 2.Διαιρέστε και τις δύο πλευρές της εξίσωσης με
α) cos x ≠ 0;
β) cos 2 x ≠ 0;
και πάρτε την εξίσωση για το tan x:
α) a tan x + b = 0;
β) a tan 2 x + b arctan x + c = 0.
Βήμα 3.Λύστε την εξίσωση χρησιμοποιώντας γνωστές μεθόδους.
Παράδειγμα.
5sin 2 x + 3sin x cos x – 4 = 0.
Λύση.
1) 5sin 2 x + 3sin x · cos x – 4(sin 2 x + cos 2 x) = 0;
5sin 2 x + 3sin x · cos x – 4sin² x – 4cos 2 x = 0;
sin 2 x + 3sin x · cos x – 4cos 2 x = 0/cos 2 x ≠ 0.
2) tg 2 x + 3tg x – 4 = 0.
3) Έστω tg x = t, τότε
t 2 + 3t – 4 = 0;
t = 1 ή t = -4, που σημαίνει
tg x = 1 ή tg x = -4.
Από την πρώτη εξίσωση x = π/4 + πn, n Є Z; από τη δεύτερη εξίσωση x = -arctg 4 + πk, k Є Z.
Απάντηση: x = π/4 + πn, n Є Z; x = -arctg 4 + πk, k Є Z.
V. Μέθοδος μετασχηματισμού εξίσωσης με χρήση τριγωνομετρικών τύπων
Διάγραμμα λύσης
Βήμα 1.Χρησιμοποιώντας όλα τα είδη τριγωνομετρικούς τύπους, ανάγετε αυτήν την εξίσωση σε μια εξίσωση που επιλύεται με τις μεθόδους I, II, III, IV.
Βήμα 2.Λύστε την εξίσωση που προκύπτει χρησιμοποιώντας γνωστές μεθόδους.
Παράδειγμα.
αμαρτία x + αμαρτία 2x + αμαρτία 3x = 0.
Λύση.
1) (αμαρτία x + αμαρτία 3x) + αμαρτία 2x = 0;
2sin 2x cos x + sin 2x = 0.
2) αμαρτία 2x (2cos x + 1) = 0;
sin 2x = 0 ή 2cos x + 1 = 0;
Από την πρώτη εξίσωση 2x = π/2 + πn, n Є Z; από τη δεύτερη εξίσωση cos x = -1/2.
Έχουμε x = π/4 + πn/2, n Є Z; από τη δεύτερη εξίσωση x = ±(π – π/3) + 2πk, k Є Z.
Ως αποτέλεσμα, x = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.
Απάντηση: x = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.
Η ικανότητα και η ικανότητα επίλυσης τριγωνομετρικών εξισώσεων είναι πολύ  σημαντικό, η ανάπτυξή τους απαιτεί σημαντική προσπάθεια, τόσο από την πλευρά του μαθητή όσο και από την πλευρά του δασκάλου.
σημαντικό, η ανάπτυξή τους απαιτεί σημαντική προσπάθεια, τόσο από την πλευρά του μαθητή όσο και από την πλευρά του δασκάλου.
Πολλά προβλήματα στερεομετρίας, φυσικής κ.λπ. σχετίζονται με τη λύση τριγωνομετρικών εξισώσεων.Η διαδικασία επίλυσης τέτοιων προβλημάτων ενσωματώνει πολλές από τις γνώσεις και τις δεξιότητες που αποκτώνται με τη μελέτη των στοιχείων της τριγωνομετρίας.
Οι τριγωνομετρικές εξισώσεις κατέχουν σημαντική θέση στη διαδικασία της εκμάθησης των μαθηματικών και της προσωπικής ανάπτυξης γενικότερα.
Έχετε ακόμα ερωτήσεις; Δεν ξέρετε πώς να λύσετε τριγωνομετρικές εξισώσεις;
Για να λάβετε βοήθεια από έναν δάσκαλο, εγγραφείτε.
Το πρώτο μάθημα είναι δωρεάν!
ιστοσελίδα, όταν αντιγράφετε υλικό εν όλω ή εν μέρει, απαιτείται σύνδεσμος προς την πηγή.
ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΣΗΣ ΜΟΣΧΑΣ
ΕΠΑΓΓΕΛΜΑΤΙΚΟΣ ΚΡΑΤΙΚΟΥ ΠΡΟΫΠΟΛΟΓΙΣΜΟΥ
ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ στη Μόσχα
"Πολυτεχνικό Κολλέγιο Νο. 47 με το όνομα V.G. Fedorov"
Μάθημα
στον κλάδο των Μαθηματικών
"Τριγωνομετρικές εξισώσεις ανάγονται σε τετραγωνικό"
Δάσκαλος
Protasevich Olga Nikolaevna
ΕΠΑΓΓΕΛΜΑ: Μηχανικός υλικού και λογισμικού
ΠΕΙΘΑΡΧΙΑ: Μαθηματικά
ΚΑΛΑ : 1
ΕΞΑΜΗΝΟ : 2
ΟΜΑΔΑ :
Θέμα μαθήματος:
"Τριγωνομετρικές εξισώσεις ανάγονται σε τετραγωνικές εξισώσεις."
Τύπος μαθήματος: συνδυασμένο μάθημα
Μορφή μαθήματος: συλλογική εκπαίδευση σύμφωνα με τη μεθοδολογία του Β.Κ. Ντιατσένκο
(εκπαίδευση σε συστήματα μικρών ομάδων)
Στόχοι μαθήματος:
Εκπαιδευτικός – εξετάστε γενικές προσεγγίσεις, συνοψίστε πληροφορίες σχετικά με τους τύπους και τις μεθόδους επίλυσης τριγωνομετρικών εξισώσεων που μπορούν να αναχθούν σε τετραγωνικές. να αναπτύξουν δεξιότητες και ικανότητες εφαρμογής γνώσεων κατά την επίλυση βασικών εξισώσεων και την εφαρμογή της αποκτηθείσας γνώσης σε επαγγελματικές δραστηριότητες.
Αναπτυξιακή – προώθηση της ανάπτυξης λογική σκέψημεταξύ των μαθητών, να αναπτύξουν τις δεξιότητες ανάλυσης, λογικής, σύγκρισης, εξαγωγής συμπερασμάτων, κατανόησης του υλικού.
Εκπαιδευτικός – ενθάρρυνση του γνωστικού ενδιαφέροντος, στοιχείων κουλτούρας επικοινωνίας, ενθάρρυνση των μαθητών να ξεπεράσουν δυσκολίες στη διαδικασία της νοητικής δραστηριότητας, ανάπτυξη δεξιοτήτων για εργασία σε ομάδα εργασίας και εκπαίδευσης.
Στόχος μαθήματος:
Να εξοικειωθούν οι μαθητές με τους κύριους τύπους και μεθόδους επίλυσης τριγωνομετρικών εξισώσεων που μπορούν να αναχθούν σε τετραγωνικές.
Υποστήριξη (πόροι):
Υλικό: υπολογιστής, προβολέας πολυμέσων.
Λογισμικό:MicrosoftΠροέχω.
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ:
Τετραγωνική εξίσωση; απλές τριγωνομετρικές εξισώσεις. αντίστροφες τριγωνομετρικές συναρτήσεις. τριγωνομετρικές εξισώσεις ανάγονται σε τετραγωνικές.
Βιβλιογραφία:
Μπασμάκοφ Μ.Ι. Μαθηματικά: εγχειρίδιο πρωτοβάθμιας και δευτεροβάθμιας εκπαίδευσης επαγγελματική εκπαίδευση.- Μ.; "Ακαδημία", 2010. - 256 σελ.
Dyachenko V.K. - M.; «Δημόσια Εκπαίδευση», 2001. - 496 s.
Μπασμάκοφ Μ.Ι. Μαθηματικά: ένα βιβλίο για δασκάλους. Μεθοδολογικό εγχειρίδιο - M.; « Ακαδημία», 2013 - 224 σελ.
Υλικά τοποθεσίαςκοινωνικό και παιδαγωγικό κίνημα για τη δημιουργία ενός συλλογικού τρόπου διδασκαλίας:www.kco-kras.ru.
Βήματα μαθήματος
Οργάνωση χρόνου.
Έλεγχος εργασιών για το σπίτι.
Ενημέρωση βασικών γνώσεων.
Εκμάθηση νέου υλικού.
Εμπέδωση και συστηματοποίηση της αποκτηθείσας γνώσης.
Αντανάκλαση. Συνοψίζοντας. Εργασία για το σπίτι.
Κατά τη διάρκεια των μαθημάτων
Οργάνωση χρόνου.
Ο δάσκαλος θέτει τους στόχους του μαθήματος για τους μαθητές:
1) Εισάγετε τους κύριους τύπους τριγωνομετρικών εξισώσεων που μπορούν να αναχθούν σε τετραγωνικές.
2) Εισάγετε τυπικές μεθόδους για την επίλυση τριγωνομετρικών εξισώσεων που μπορούν να αναχθούν σε τετραγωνικές.
3) Διδάξτε πώς να εφαρμόζετε τις αποκτηθείσες γνώσεις και δεξιότητες για την επίλυση τυπικών εξισώσεων.
4) Διδάξτε πώς να εργάζεστε με τις πληροφορίες που παρουσιάζονται στο διάφορες μορφές, ασκούν αμοιβαίο έλεγχο και αυτοέλεγχο, εφαρμόζουν τις αποκτηθείσες γνώσεις σε επαγγελματικές δραστηριότητες.
II . Έλεγχος εργασιών για το σπίτι.
Ο δάσκαλος περιλαμβάνει μια παρουσίαση «Εργασία για το σπίτι», σύμφωνα με την οποία οι μαθητές ελέγχουν ανεξάρτητα την εργασία τους και, εάν χρειάζεται, κάνουν τροποποιήσεις και διορθώσεις στην εργασία.
Μετά από αίτημα των μαθητών, ο δάσκαλος σχολιάζει τις λύσεις των εξισώσεων που προκάλεσαν δυσκολίες και μετά ανακοινώνει τα ονόματα των μαθητών που στο τέλος του μαθήματος παραδίδουν τα τετράδιά τους για έλεγχο.
№ 1
Απάντηση:
№ 2
Απάντηση:
№ 3
Απάντηση:
№ 4
επειδή τότε η εξίσωση δεν έχει ρίζες
Απάντηση: χωρίς ρίζες
№ 5
Απάντηση:
№ 6
Απάντηση:
III . Ενημέρωση βασικών γνώσεων.
Ο δάσκαλος σχηματίζει ομάδες/ζεύγη μελέτης και προτείνει να χρησιμοποιήσετε τις παρεχόμενες φόρμες για να δημιουργήσετε μια αντιστοιχία μεταξύ των εξισώσεων και των απαντήσεων: «Μπροστά σας είναι μια διαφάνεια με μια εκπαιδευτική εργασία. Αντιστοιχίστε τις εξισώσεις (αριστερή πλευρά του πίνακα) με τις απαντήσεις (δεξιά πλευρά του πίνακα). Σημειώστε τους αριθμούς των σωστών ζευγών δηλώσεων στο τετράδιό σας.»
Οι καθορισμένες εργασίες αντιγράφονται στην παρουσίαση που περιλαμβάνεται.
Αγώνας
p/p
Η εξίσωση
p/p
Απάντηση
χωρίς ρίζες
Στο τέλος της εργασίας, ο δάσκαλος παίρνει μετωπικές συνεντεύξεις από τους εκπροσώπους της ομάδας και μετά ανοίγει τη σελίδα παρουσίασης με τις σωστές λύσεις.
Σωστές απαντήσεις
p/p
Η εξίσωση
p/p
Απάντηση
χωρίς ρίζες
χωρίς ρίζες
11.
13.
10.
12.
IV . Εκμάθηση νέου υλικού.
Ο δάσκαλος περιλαμβάνει παρουσίαση νέου υλικού «Τριγωνομετρικές εξισώσεις ανηγμένες σε τετραγωνικές. Τύποι εξισώσεων και μέθοδοι για τις λύσεις τους."
Καλεί τους μαθητές να σημειώσουν τα απαραίτητα σημεία και αρχίζει να σχολιάζει κάθε διαφάνεια και μετά ενεργοποιούν την παρουσίαση.
Ας εισαγάγουμε την έννοια:
Γενική άποψη τετραγωνικής εξίσωσης:
1 τύπος τριγωνομετρικών εξισώσεων που μπορούν να αναχθούν σε τετραγωνικές εξισώσεις – εξισώσεις που είναι αλγεβρικές σε σχέση με μία από τις τριγωνομετρικές συναρτήσεις.
Ο δάσκαλος εξηγεί τις λύσεις.
1. Άμεση αντικατάσταση
Αντικατάσταση ,
Και
χωρίς ρίζες
Απάντηση:
Οι εξισώσεις της μορφής έχουν παρόμοια λύση
Αντικατάσταση
Αντικατάσταση
2. Εξισώσεις που απαιτούν μετατροπή χρησιμοποιώντας τον τύπο της τριγωνομετρικής μονάδας
Αντικατάσταση , τότε η εξίσωση παίρνει τη μορφή
Και
χωρίς ρίζες
Απάντηση:
Οι εξισώσεις της μορφής έχουν παρόμοια λύση:
θα αντικαταστήσουμε , χρησιμοποιώντας τον τύπο της τριγωνομετρικής μονάδας
.
Λαμβάνουμε μια εξίσωση που περιέχει μόνο μία τριγωνομετρική συνάρτηση :
Αντικατάσταση
3. Εξισώσεις που απαιτούν μετασχηματισμό χρησιμοποιώντας τον τύπο σύνδεσης tgx Και Με tgx
Εφαρμόζουμε τον τύπο:
Πολλαπλασιάστε την εξίσωση επί
Αντικατάσταση , τότε η εξίσωση παίρνει τη μορφή
Και
Απάντηση:
Τύπος 2 τριγωνομετρικές εξισώσεις αναγωγής σε δευτεροβάθμιες εξισώσεις– ομοιογενείς εξισώσεις στις οποίες κάθε όρος έχει τον ίδιο βαθμό.
Διαιρέστε την εξίσωση με
Αντικατάσταση , τότε η εξίσωση παίρνει τη μορφή
Και
Απάντηση:
Ο δάσκαλος προτείνει τη σύνοψη του υλικού που παρουσιάζεται και θέτει ερωτήσεις: «Σε πόσους τύπους χωρίζονται οι τριγωνομετρικές εξισώσεις που μπορούν να αναχθούν σε τετραγωνικές εξισώσεις; Το ονομα τους? Ονομάστε τρόπους επίλυσης τριγωνομετρικών εξισώσεων που μπορούν να αναχθούν σε τετραγωνικές.»
Ο δάσκαλος καθοδηγεί τις ενέργειες των μαθητών όταν δημιουργεί έναν αλγόριθμο για την επίλυση εξισώσεων αυτού του τύπου.
Οι τριγωνομετρικές εξισώσεις που ανάγονται σε τετραγωνικές εξισώσεις χωρίζονται σε δύο βασικούς τύπους:
tgx Και Με tgx :
Τύπος 2 – ομοιογενείς εξισώσεις στις οποίες κάθε όρος έχει τον ίδιο βαθμό:
Ο δάσκαλος κάνει μια προσαρμογή Αλγόριθμος λύσης:
1. Προσδιορίστε το είδος της εξίσωσης. Εάν χρειάζεται, μετατρέψτε την εξίσωση έτσι ώστε να υπάρχει μόνο μία τριγωνομετρική συνάρτηση. Για να το κάνετε αυτό, επιλέξτε τον επιθυμητό τύπο: ήή χωρίστε σε
2. Εισάγεται μια αντικατάσταση (για παράδειγμα, sinx = t , cosx = t , tgx = t ).
5. Γράψτε την απάντηση.
Για την εδραίωση της αποκτηθείσας γνώσης, ο δάσκαλος προτείνει τη δημιουργία αντιστοιχίας μεταξύ των εξισώσεων και των πιθανών μεθόδων επίλυσής τους: «Μπροστά σας είναι μια διαφάνεια με μια εκπαιδευτική εργασία.
1. Ταξινομήστε τις εξισώσεις σύμφωνα με μεθόδους λύσης σύμφωνα με τον παρακάτω πίνακα
(οι τυπωμένες εκδόσεις του πίνακα βρίσκονται στα γραφεία σας).
2. Εισαγάγετε τον αριθμό της μεθόδου λύσης στο κατάλληλο πλαίσιο.
Γέμισε το τραπέζι».
Η εργασία γίνεται σε ζευγάρια.
p/p
Η εξίσωση
μέθοδος
Μέθοδοι:
1) Εισαγάγετε μια νέα μεταβλητή.
2) Εισαγάγετε μια νέα μεταβλητή
3) Εισαγάγετε μια νέα μεταβλητή.
4) Μετασχηματίστε την εξίσωση χρησιμοποιώντας τον τύπο και εισαγάγετε μια νέα μεταβλητή.
5) Μετασχηματίστε την εξίσωση χρησιμοποιώντας τον τύπο, εισάγετε μια νέα μεταβλητή.
6) Διαιρέστε κάθε όρο της εξίσωσης με, εισάγετε μια νέα μεταβλητή.
7) Μετατρέψτε την εξίσωση χρησιμοποιώντας τον τύπο, πολλαπλασιάστε τους όρους της εξίσωσης επί, εισάγετε μια νέα μεταβλητή.
Η εργασία ελέγχεται με τη μορφή μετωπικής συνομιλίας.
Δάσκαλος: «Μπροστά σας είναι μια διαφάνεια με τις σωστές απαντήσεις στην εκπαιδευτική εργασία. . Ελέγξτε ελέγχοντας τις σωστές απαντήσεις στην εκπαιδευτική εργασία. Δούλεψε τα λάθη στο σημειωματάριό σου».
Τα φύλλα εργασιών συλλέγονται στο τέλος του μαθήματος.
p/p
Η εξίσωση
μέθοδος
2
4
2
1
7
1
3
5
6
3
6
2
6
VI . Εμπέδωση και συστηματοποίηση της αποκτηθείσας γνώσης.
Ο δάσκαλος καλεί τους μαθητές να συνεχίσουν να εργάζονται σε ομάδες.
Δάσκαλος: «Λύστε τις εξισώσεις. Ελέγξτε το αποτέλεσμα στο πρόγραμμα επεξεργασίας Microsoft Προέχω . Στο τέλος της λύσης, ένας εκπρόσωπος της ομάδας πηγαίνει στον μαυροπίνακα και παρουσιάζει τη λύση στην εξίσωση που συμπλήρωσε η ομάδα.» Ο δάσκαλος ελέγχει τη λύση, αξιολογεί την εργασία της ομάδας και, εάν χρειάζεται, επισημαίνει λάθη».
Δάσκαλος:
1 ) Συζητήστε ομαδικά τις λύσεις.
2) Σημειώστε τη λύση και την απάντηση που λάβατε στο τετράδιό σας.
3) Ελέγξτε το αποτέλεσμα στο πρόγραμμα επεξεργασίας Microsoft Προέχω .
4) Ενημερώστε τον δάσκαλό σας ότι είστε έτοιμοι.
5) Εξηγήστε την απόφασή σας γράφοντάς την στον πίνακα σε μέλη άλλων ομάδων.
6) Ακούστε προσεκτικά τις ομιλίες των συντρόφων σας, κάντε ερωτήσεις εάν χρειάζεται.
Οι ομάδες μελέτης που έχουν ολοκληρώσει πλήρως τις εργασίες καλούνται να ολοκληρώσουν τις εργασίες άλλων ομάδων. Οι επιτυχημένες ομάδες ανταμείβονται με αύξηση της τελικής βαθμολογίας κατά μία μονάδα.
Πρώτη ομάδα:
Εφαρμόζουμε τον τύπο:
Και
χωρίς ρίζες
επειδή
Απάντηση:
Δεύτερη ομάδα:
Εφαρμόζουμε τον τύπο:
Αντικατάσταση, τότε γίνεται η εξίσωση
Και
Απάντηση: ;
Τρίτη ομάδα:
Εφαρμόζουμε τον τύπο:
Πολλαπλασιάστε την εξίσωση επί
Αντικατάσταση, τότε γίνεται η εξίσωση
Και
Απάντηση:
Τέταρτη ομάδα:
Διαιρέστε την εξίσωση με
Αντικατάσταση, τότε γίνεται η εξίσωση
Και
Απάντηση:
Πέμπτη ομάδα:
Αντικατάσταση, τότε γίνεται η εξίσωση
Και
Απάντηση:; .
VII . Αντανάκλαση. Συνοψίζοντας. Εργασία για το σπίτι.
Δάσκαλος: Ας συνοψίσουμε τη δουλειά σας, συσχετίζοντας τα αποτελέσματα των δραστηριοτήτων σας με τον στόχο σας.
Ας επαναλάβουμε έννοιες:
«Οι τριγωνομετρικές εξισώσεις που ανάγονται σε τετραγωνικές εξισώσεις με μετασχηματισμό και αλλαγή μεταβλητής ονομάζονται τριγωνομετρικές εξισώσεις που μπορούν να αναχθούν σε δευτεροβάθμιες εξισώσεις».
Τύπος 1 – εξισώσεις, αλγεβρικές ως προς μία από τις τριγωνομετρικές συναρτήσεις:
- άμεση αντικατάσταση - αντικατάσταση ή
- εξισώσεις που απαιτούν μετατροπή χρησιμοποιώντας τον τύπο τριγωνομετρικής μονάδας.
- εξισώσεις που απαιτούν μετασχηματισμό σύμφωνα με τον τύπο σύνδεσης tgx και με tgx :
Τύπος 2 – ομοιογενείς εξισώσεις στις οποίες κάθε όρος έχει τον ίδιο βαθμό: διαιρέστε την εξίσωση με και μετά αντικαταστήστε.
Αλγόριθμος λύσης:
1. Προσδιορίστε το είδος της εξίσωσης. Εάν χρειάζεται, αναδιατάξτε την εξίσωση έτσι ώστε να περιέχει μόνο μία τριγωνομετρική συνάρτηση.
Για να το κάνετε αυτό, επιλέξτε τον επιθυμητό τύπο:
ή ή χωρίστε σε
2. Εισάγεται μια αντικατάσταση (για παράδειγμα, sinx = t , cosx = t , tgx = t ).
3. Λύστε την δευτεροβάθμια εξίσωση.
4. Γίνεται η αντίστροφη αντικατάσταση και λύνεται η απλούστερη τριγωνομετρική εξίσωση.
5. Γράψτε την απάντηση.
Ο δάσκαλος αξιολογεί τη δουλειά των μαθητών, ομάδες μελέτηςκαι ανακοινώνει τις βαθμολογίες.
Δάσκαλος: «Γράψε την εργασία σου: Bashmakov M.I. Μαθηματικά: εγχειρίδιο για επαγγελματίες πρωτοβάθμιας και δευτεροβάθμιας εκπαίδευσης. εκπαίδευση. – M.; «Ακαδημία», 2010. Σελ. 114-115. Στον αριθμό 10, λύστε τις εξισώσεις με αριθμό 4,5,7,9. σελ. 118. Ελέγξτε το αποτέλεσμα στο πρόγραμμα επεξεργασίας Microsoft Προέχω ».