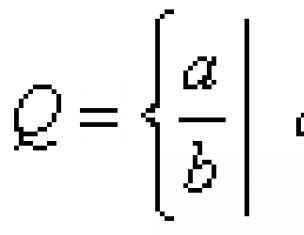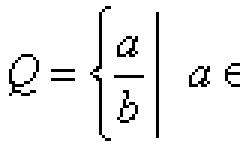1 круг определение дуга окружности центральный угол. Вписанная и описанная окружности. Центральные и вписанные углы

Пусть
 произвольная точка эллипса. Имеем:
,
. Из определения эллипса

, (1.29)

или  искомое уравнение эллипса, которое неудобно для использования. Из последнего равенства следует, что .Так как
, то можем обе части уравнения возвести в квадрат и после эквивалентных преобразований получим:
. Следовательно,. Введем новую переменную
. Имеем:
. Из этого равенства следует, что

. (1.30)

Уравнение (1.30) называется каноническим (простейшим) уравнением эллипса. Это уравнение является уравнением второго порядка. Таким образом, любая точка эллипса, удовлетворяющая уравнению (1.29), удовлетворяет и уравнению (1.30). Докажем, что все точки плоскости, координаты которых удовлетворяют уравнению (1.30), являются точками эллипса, т. е. их координаты удовлетворяют уравнению (1.29).

Для фокального радиуса выполняется соотношение
. Из уравнения (1.30) имеем:
. Поэтому
, или
. Аналогично находим, что
. Следовательно,
.

Эллипс симметричен относительно координатных осей, так как содержит только четные степени и, и относительно начала координат. Оси симметрии эллипса называются его осями, а центр симметрии центром эллипса.

Эллипс пересекает координатные оси в точках
,
,
,
. Эти точки называются вершинами эллипса. При
эллипс вырождается в окружность радиусоми центром в начале координат. Вершины эллипса ограничивают на осях отрезки длиной
и
, причем
(это следует из того, что
).

Величины иназываются большой и малой полуосями эллипса, оси эллипса соответственно большой и малой осью.

Определение. Эксцентриситетом эллипса называется отношение, где половина расстояния между фокусами,  большая полуось, т. е.

. (1.31)

Учитывая, что
, получим
. Так как

, то
. Если
, т. е. эллипс приближается к окружности, то
. Если
, ак нулю не стремится, то эллипс вытянут вдоль большой оси. Таким образом, эксцентриситет эллипса характеризует меру его вытянутости вдоль большой оси.

Если фокусы эллипса
и
расположены на оси ординат, то в этом случае
и большой является полуось. Уравнение эллипса также имеет вид (1.30), но
, а его эксцентриситет вычисляется по формуле
.

П р и м е р 14. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, зная, что расстояние между его фокусами
и эксцентриситет
.

Решение. Половина расстояния между фокусами
. Фокусы эллипса расположены на оси абсцисс, поэтому большой полуосью является. Из (1.31) следует, что
. Тогда. Таким образом, уравнение эллипса имеет вид
.

П р и м е р 15. Дан эллипс
. Найти его полуоси, фокусы, эксцентриситет.

Решение. Приведем уравнение эллипса к каноническому виду. Для этого обе части уравнения разделим на 45, получим
. Таким образом, его полуось
,
. Большой полуосью является полуось, поэтому фокусы эллипса расположены на оси ординат и

, следовательно, фокусы находятся в точках
и
. Эксцентриситет эллипса равен отношению половины расстояния между фокусами к большой полуоси, т. е.
.

П р и м е р 16. Вычислить площадь четырехугольника
, две вершиныикоторого лежат в фокусах эллипса
, две другиеи
совпадают с концами его малой оси.

Решение. Каноническое уравнение эллипса имеет вид
, поэтому
,
. Следовательно, вершины четырехугольникаи
имеют соответственно координаты
и
. Найдем координаты вершини. Так как
, то
,
. Полученный четырехугольник симметричен относительно координатных осей и относительно начала координат, следовательно,

.

Лекция: Окружность и круг

Окружность – это замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра.

В повседневной жизни Вы не раз встречали окружность. Именно её описывает часовая и секундная стрелка, именно форму окружности имеет гимнастический обруч.

А теперь представьте, что Вы нарисовали окружность на листке бумаги и захотели её разукрасить.

Так вот все разукрашенное пространство, ограниченное окружностью – это и есть круг.

Центр – это точка, которая равноудалена от всех точек окружности. Центр круга и окружности обозначается буквой О.

Радиус – это расстояние от центра до окружности (R).

Диаметр – это отрезок, проходящий через центр, который соединяет все точки окружности (d). Более того, диаметр равен двум радиусам: d = 2R.

Хорда – отрезок, который соединяет любые две точки на окружности. Диаметр является частным случаем хорды.

Чтобы найти длину окружности, необходимо воспользоваться формулой:

l =2 πR

Обратите внимание, длина окружности, площадь зависят только от радиуса данной окружности.

Площадь круга можно найти по следующей формуле:

S =πR 2 .

Хотелось бы обратить Ваше внимание на число «Пи». Данное значение было найдено как раз с помощью окружности. Для этого её длину разделили на два радиуса, и таким образом получилось число «Пи».

Если круг разбить на некоторые части двумя радиусами, то такие части будут называться секторами. Каждый сектор имеет свою градусную меру – градусную меру той дуги, на которую опирается.

Чтобы найти длину дуги, необходимо воспользоваться формулой:

2. Используя радианную меру:

Если вершина некоторого угла опирается на центр окружности, а его лучи пересекают окружность, то такой угол называется центральным.

Если некоторые две хорды пересекаются в некоторой точке, то их отрезки пропорциональны:

Эта статья содержит минимальный набор сведений об окружности, необходимый для успешной сдачи ЕГЭ по математике.

Окружностью называется множество точек, расположенных на одинаковом расстоянии от данной точки, которая называется центром окружности.

Для любой точки , лежащей на окружности выполняется равенство (Длина отрезка равна радиусу окружности.

Отрезок, соединяющий две точки окружности называется хордой.

Хорда, проходящая через центр окружности называется диаметром окружности ().

Длина окружности:

Площадь круга:

Дуга окружности:

Часть окружности, заключенная между двумя ее точками называется дугой окружности. Две точки окружности определяют две дуги. Хорда стягивает две дуги: и . Равные хорды стягивают равные дуги.

Угол между двумя радиусами называется центральным углом :

Чтобы найти длину дуги , составляем пропорцию:

а) угол дан в градусах:

б) угол дан в радианах:

Диаметр, перпендикулярный хорде , делит эту хорду и дуги, которые она стягивает пополам:

Если хорды и окружности пересекаются в точке , то произведения отрезков хорд, на которые они делятся точкой равны между собой:

Касательная к окружности.

Прямая, имеющая с окружностью одну общую точку называется касательной к окружности. Прямая, имеющая с окружностью две общие точки называется секущей.

Касательная к окружности перпендикулярна радиусу, проведенному к точке касания.

Если из данной точки проведены к окружности две касательные, то отрезки касательных равны между собой и центр окружности лежит на биссектрисе угла с вершиной в этой точке:

Если из данной точки проведены к окружности касательная и секущая, то квадрат длины отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть :

Следствие: произведение всего отрезка одной секущей на его внешнюю часть равно произведению всего отрезка другой секущей на его внешнюю часть :

Углы в окружности.

Градусная мера центрального угла равна градусной мере дуги, на которую он опирается:

Угол, вершина которого лежит на окружности, а стороны содержат хорды, называется вписанным углом . Вписанный угол измеряется половиной дуги, на которую он опирается:

∠∠

Вписанный угол, опирающийся на диаметр, прямой:

∠∠∠

Вписанные углы, опирающиеся на одну дугу, равны :

Вписанные углы, опирающиеся на одну хорду равны или их сумма равна

∠∠

Вершины треугольников с заданным основанием и равными углами при вершине лежат на одной окружности:

Угол между двумя хордами (угол с вершиной внутри окружности) равен полусумме угловых величин дуг окружности, заключенных внутри данного угла и внутри вертикального угла.

∠ ∠∠(⌣ ⌣ )

Угол между двумя секущими (угол с вершиной вне окружности) равен полуразности угловых величин дуг окружности, заключенных внутри угла.

∠ ∠∠(⌣ ⌣ )

Вписанная окружность.

Окружность называется вписанной в многоугольник , если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.

Не во всякий многоугольник можно вписать окружность.

Площадь многоугольника, в который вписана окружность можно найти по формуле

здесь - полупериметр многоугольника, - радиус вписанной окружности.

Отсюда радиус вписанной окружности равен

Если в выпуклый четырехугольник вписана окружность, то суммы длин противоположных сторон равны . Обратно: если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в четырехугольник можно вписать окружность:

В любой треугольник можно вписать окружность, притом только одну. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.

Радиус вписанной окружности равен . Здесь

Описанная окружность.

Окружность называется описанной около многоугольника , если она проходит через все вершины многоугольника. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров сторон многоугольника. Радиус вычисляется как радиус окружности, описанной около треугольника, определенного любыми тремя вершинами данного многоугольника:

Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна .

Около любого треугольника можно описать окружность, притом только одну. Ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника:

Радиус описанной окружности вычисляется по формулам:

Где - длины сторон треугольника, - его площадь.

Теорема Птолемея

Во вписанном четырехугольнике произведение диагоналей равно сумме произведений его противоположных сторон:

В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, \(\frac{π}{2}, \frac{π}{3}, \frac{7π}{4}, 10π, -\frac{29π}{6}\)) разбирается в .

Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют , расставленным по следующим правилам:

1) Начало отсчета находится в крайней правой точке окружности;

2) Против часовой стрелки - положительное направление; по часовой – отрицательное;

3) Если в положительном направлении отложить на окружности расстояние \(t\), то мы попадем в точку со значением \(t\);

4) Если в отрицательном направлении отложить на окружности расстояние \(t\), то мы попадем в точку со значением \(–t\).

Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.

Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен \(1\). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках \(1\) и \(-1\).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).

Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы \(l=2πR\) мы получим:

Длина числовой окружности равна \(2π\) или примерно \(6,28\).

А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» - точка, которая соответствует этому числу.

Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности - каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?

Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте \(1\) на оси \(x\) и \(0\) на окружности – это точки на разных объектах.

Какие точки соответствуют числам \(1\), \(2\) и т.д?

Помните, мы приняли, что у числовой окружности радиус равен \(1\)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.

Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу \(2\), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы \(3\) – расстояние равное трем радиусам и т.д.

При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.

2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.

К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: \(2π\). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли