- Η απόσταση από το κέντρο του κύκλου στην ευθεία είναι μεγαλύτερη από την ακτίνα.Στην περίπτωση αυτή, όλα τα σημεία της ευθείας βρίσκονται εκτός του κύκλου.
- Η απόσταση από το κέντρο του κύκλου στην ευθεία είναι μικρότερη από την ακτίνα.Στην περίπτωση αυτή, η ευθεία έχει σημεία που βρίσκονται μέσα στον κύκλο και εφόσον η ευθεία είναι άπειρη και στις δύο κατευθύνσεις, τέμνεται από τον κύκλο σε 2 σημεία.
- Η απόσταση από το κέντρο του κύκλου στην ευθεία είναι ίση με την ακτίνα.Η ευθεία είναι εφαπτομένη.
Μια ευθεία γραμμή που μοιράζεται μόνο έναν κύκλο με έναν κύκλο κοινό σημέιο, που ονομάζεται εφαπτομένη γραμμήστον κύκλο.
Το κοινό σημείο ονομάζεται σε αυτή την περίπτωση σημείο επαφής.
Η πιθανότητα ύπαρξης μιας εφαπτομένης, και, επιπλέον, να τραβηχτεί από οποιοδήποτε σημείο του κύκλου ως σημείο εφαπτομένης, αποδεικνύεται από το ακόλουθο θεώρημα.
Θεώρημα. Αν μια ευθεία είναι κάθετη στην ακτίνα στο άκρο της που βρίσκεται στον κύκλο, τότε αυτή η ευθεία είναι εφαπτομένη.
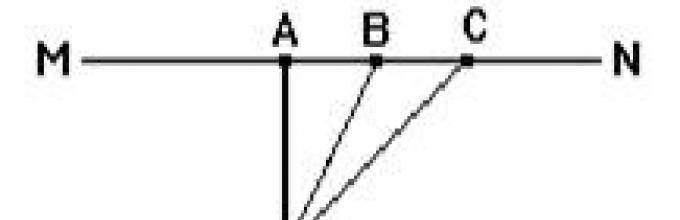
Έστω Ο (εικ) το κέντρο κάποιου κύκλου και ΟΑ κάποια από την ακτίνα του. Μέσα από το άκρο του Α τραβάμε ΜΝ ^ ΟΑ.
Απαιτείται να αποδειχθεί ότι η ευθεία ΜΝ είναι εφαπτομένη, δηλ. ότι αυτή η ευθεία έχει μόνο ένα κοινό σημείο Α με τον κύκλο.

Ας υποθέσουμε το αντίθετο: ας έχει το MN ένα άλλο κοινό σημείο με τον κύκλο, για παράδειγμα το B.
Τότε η ευθεία ΟΒ θα ήταν μια ακτίνα και επομένως ίση με την ΟΑ.
Αλλά αυτό δεν μπορεί να είναι, αφού αν το ΟΑ είναι κάθετο, τότε το ΟΒ πρέπει να είναι κεκλιμένο στο ΜΝ, και το κεκλιμένο είναι μεγαλύτερο από την κάθετο.
Θεώρημα αντιστροφής. Εάν μια ευθεία εφάπτεται σε έναν κύκλο, τότε η ακτίνα που τραβιέται στο σημείο εφαπτομένης είναι κάθετη σε αυτόν.
Έστω MN η εφαπτομένη στον κύκλο, A το σημείο εφαπτομένης και O το κέντρο του κύκλου.
Απαιτείται να αποδειχθεί ότι ο ΟΑ^ΜΝ.
Ας υποθέσουμε το αντίθετο, δηλ. Ας υποθέσουμε ότι η κάθετη που έπεσε από το Ο στο ΜΝ δεν θα είναι ΟΑ, αλλά κάποια άλλη ευθεία, για παράδειγμα, ΟΒ.
Ας πάρουμε BC = AB και ας πραγματοποιήσουμε OS.
Τότε το ΟΑ και το ΟΣ θα είναι κεκλιμένα, εξίσου απομακρυσμένα από την κάθετη ΟΒ, και επομένως ΟΣ = ΟΑ.
Από αυτό προκύπτει ότι ο κύκλος, λαμβάνοντας υπόψη την υπόθεσή μας, θα έχει δύο κοινά σημεία με την ευθεία ΜΝ: Α και Γ, δηλ. Το MN δεν θα είναι μια εφαπτομένη, αλλά μια διατομή, η οποία έρχεται σε αντίθεση με την προϋπόθεση.
Συνέπεια. Μέσα από οποιοδήποτε δεδομένο σημείο ενός κύκλου μπορεί κανείς να σχεδιάσει μια εφαπτομένη σε αυτόν τον κύκλο, και μόνο μία, αφού μέσω αυτού του σημείου μπορεί κανείς να σχεδιάσει μια κάθετη, και μόνο μια, στην ακτίνα που σύρεται σε αυτόν.
Θεώρημα. Μια εφαπτομένη παράλληλη σε μια χορδή διαιρεί το τόξο που υποτάσσεται από τη χορδή στο μισό στο σημείο επαφής.
Αφήστε την ευθεία ΑΒ (εικ.) να αγγίξει τον κύκλο στο σημείο Μ και να είναι παράλληλη με τη χορδή CD.
Πρέπει να αποδείξουμε ότι ÈCM = ÈMD.

Σχεδιάζοντας τη διάμετρο ME στο σημείο εφαπτομένης, λαμβάνουμε: EM ^ AB, και επομένως EM ^ CB.
Επομένως CM=MD.
Εργο.Μέσα από ένα δεδομένο σημείο σχεδιάστε μια εφαπτομένη σε έναν δεδομένο κύκλο.
Αν δεδομένο σημείοείναι σε έναν κύκλο, στη συνέχεια τραβήξτε μια ακτίνα μέσω αυτού και μια κάθετη ευθεία γραμμή στο άκρο της ακτίνας. Αυτή η γραμμή θα είναι η επιθυμητή εφαπτομένη.
Ας εξετάσουμε την περίπτωση που το σημείο δίνεται εκτός του κύκλου.
Έστω ότι απαιτείται (Εικ.) να σχεδιάσουμε μια εφαπτομένη σε έναν κύκλο με κέντρο το Ο έως το σημείο Α.
Για να γίνει αυτό, από το σημείο Α, ως κέντρο, περιγράφουμε ένα τόξο με ακτίνα ΑΟ και από το σημείο Ο, ως κέντρο, τέμνουμε αυτό το τόξο στα σημεία Β και Γ με ένα άνοιγμα πυξίδας ίσο με τη διάμετρο του δεδομένου κύκλου. .
Έχοντας στη συνέχεια σχεδιάσει τις συγχορδίες ΟΒ και ΟΣ, συνδέουμε το σημείο Α με τα σημεία Δ και Ε, στα οποία αυτές οι συγχορδίες τέμνονται με τον δεδομένο κύκλο.
Οι γραμμές AD και AE εφάπτονται στον κύκλο O.

Πράγματι, από την κατασκευή είναι σαφές ότι οι σωλήνες AOB και AOC είναι ισοσκελές (AO = AB = AC) με τις βάσεις OB και OS ίσες με τη διάμετρο του κύκλου O.
Δεδομένου ότι το OD και το OE είναι ακτίνες, τότε το D είναι το μέσο του OB και το E είναι το μέσο του OS, που σημαίνει ότι το AD και το AE είναι διάμεσοι που έλκονται στις βάσεις των ισοσκελές σωλήνων και επομένως είναι κάθετες σε αυτές τις βάσεις. Αν οι ευθείες ΔΑ και ΕΑ είναι κάθετες στις ακτίνες ΟΔ και ΟΕ, τότε είναι εφαπτομένες.
Συνέπεια. Δύο εφαπτομένες που σχεδιάζονται από ένα σημείο σε έναν κύκλο είναι ίσες και σχηματίζουν ίσες γωνίεςμε μια ευθεία γραμμή που συνδέει αυτό το σημείο με το κέντρο.
Άρα AD=AE και ÐOAD = ÐOAE (Σχ.), επειδή τα ορθογώνια tr-ki AOD και AOE, που έχουν κοινή υποτείνουσα AO και ίσα σκέλη OD και OE (ως ακτίνες), είναι ίσα.
Σημειώστε ότι εδώ η λέξη «εφαπτομένη» σημαίνει το πραγματικό «εφαπτόμενο τμήμα» από ένα δεδομένο σημείο στο σημείο επαφής.
Εργο.Σχεδιάστε μια εφαπτομένη σε δεδομένο κύκλο O παράλληλη σε μια δεδομένη ευθεία ΑΒ (Εικ.).
Κατεβάζουμε μια κάθετη ΟΣ στην ΑΒ από το κέντρο Ο και μέσω του σημείου Δ, στο οποίο αυτή η κάθετη τέμνει τον κύκλο, σχεδιάζουμε EF || ΑΒ.
Η εφαπτομένη που αναζητούμε θα είναι η ΕΦ.

Πράγματι, αφού OS ^ AB και EF || AB, μετά EF ^ OD, και η ευθεία κάθετη στην ακτίνα στο άκρο της που βρίσκεται στον κύκλο είναι μια εφαπτομένη.
Εργο.Σχεδιάστε μια κοινή εφαπτομένη σε δύο κύκλους O και O 1 (Εικ.).

Ανάλυση. Ας υποθέσουμε ότι το πρόβλημα έχει λυθεί.
Έστω ΑΒ η κοινή εφαπτομένη, Α και Β τα σημεία εφαπτομένης.
Προφανώς, αν βρούμε ένα από αυτά τα σημεία, για παράδειγμα, το Α, τότε μπορούμε εύκολα να βρούμε το άλλο.
Ας σχεδιάσουμε τις ακτίνες OA και O 1 B. Αυτές οι ακτίνες, όντας κάθετες στην κοινή εφαπτομένη, είναι παράλληλες μεταξύ τους.
Επομένως, αν από το O 1 αντλήσουμε O 1 C || BA, τότε ο αγωγός OCO 1 θα είναι ορθογώνιος στην κορυφή C.
Ως αποτέλεσμα, εάν περιγράψουμε έναν κύκλο από το Ο ως το κέντρο με ακτίνα OS, τότε θα αγγίξει την ευθεία γραμμή O 1 C στο σημείο C.
Η ακτίνα αυτού του βοηθητικού κύκλου είναι γνωστή: είναι ίση με OA – CA = OA - O 1 B, δηλ. ισούται με τη διαφορά μεταξύ των ακτίνων αυτών των κύκλων.
Κατασκευή.Από το κέντρο Ο περιγράφουμε έναν κύκλο με ακτίνα ίση με τη διαφορά αυτών των ακτίνων.
Από το O 1 σχεδιάζουμε μια εφαπτομένη O 1 C σε αυτόν τον κύκλο (με τον τρόπο που υποδεικνύεται στο προηγούμενο πρόβλημα).
Μέσω του εφαπτομενικού σημείου C σχεδιάζουμε την ακτίνα OS και τη συνεχίζουμε μέχρι να συναντήσει τον δοσμένο κύκλο στο σημείο Α. Τέλος, από το Α τραβάμε το ΑΒ παράλληλο στο CO 1.
Με τον ίδιο ακριβώς τρόπο μπορούμε να κατασκευάσουμε μια άλλη κοινή εφαπτομένη A 1 B 1 (Εικ.). Οι ευθείες γραμμές ΑΒ και Α 1 Β 1 ονομάζονται εξωτερικόςκοινές εφαπτομένες.
Μπορείτε να ξοδέψετε άλλα δύο εσωτερικόςεφαπτομένες ως εξής:

Ανάλυση.Ας υποθέσουμε ότι το πρόβλημα έχει λυθεί (Εικ.). Έστω ΑΒ η επιθυμητή εφαπτομένη.
Ας σχεδιάσουμε τις ακτίνες OA και O 1 B στα εφαπτομενικά σημεία A και B. Επειδή αυτές οι ακτίνες είναι και οι δύο κάθετες στην κοινή εφαπτομένη, είναι παράλληλες μεταξύ τους.
Επομένως, αν από το O 1 αντλήσουμε O 1 C || BA και συνεχίστε το OA στο σημείο C, τότε το OS θα είναι κάθετο στο O 1 C.
Ως αποτέλεσμα, ο κύκλος που περιγράφεται από την ακτίνα OS από το σημείο O ως κέντρο θα αγγίξει την ευθεία O 1 C στο σημείο C.
Η ακτίνα αυτού του βοηθητικού κύκλου είναι γνωστή: είναι ίση με OA+AC = OA+O 1 B, δηλ. ισούται με το άθροισμα των ακτίνων των δοσμένων κύκλων.
Κατασκευή.Από το Ο ως κέντρο, περιγράφουμε έναν κύκλο με ακτίνα ίση με το άθροισμα αυτών των ακτίνων.
Από το O 1 σχεδιάζουμε μια εφαπτομένη O 1 C σε αυτόν τον κύκλο.
Συνδέουμε το σημείο επαφής C με το Ο.
Τέλος, μέσω του σημείου Α, στο οποίο το OS τέμνει τον δεδομένο κύκλο, σχεδιάζουμε AB = O 1 C.
Με παρόμοιο τρόπο μπορούμε να κατασκευάσουμε μια άλλη εσωτερική εφαπτομένη A 1 B 1.
Γενικός ορισμός της εφαπτομένης
Έστω μια εφαπτομένη AT και μια τέμνουσα AM να συρθούν μέσω του σημείου Α σε έναν κύκλο με κέντρο (Εικ.).
Ας περιστρέψουμε αυτήν την τομή γύρω από το σημείο Α έτσι ώστε το άλλο σημείο τομής Β να πλησιάζει όλο και πιο κοντά στο Α.

Τότε η κάθετη OD, χαμηλωμένη από το κέντρο προς την τομή, θα πλησιάζει την ακτίνα OA όλο και περισσότερο και η γωνία AOD μπορεί να γίνει μικρότερη από οποιαδήποτε μικρή γωνία.
Η γωνία ΜΑΤ που σχηματίζεται από την τέμνουσα και την εφαπτομένη είναι ίση με τη γωνία AOD (λόγω της καθετότητας των πλευρών τους).
Επομένως, καθώς το σημείο Β πλησιάζει το Α επ' αόριστον, η γωνία MAT μπορεί επίσης να γίνει αυθαίρετα μικρή.
Αυτό εκφράζεται με άλλα λόγια ως εξής:
εφαπτομένη είναι η οριακή θέση στην οποία τείνει μια τομή που σύρεται μέσω ενός σημείου εφαπτομένης όταν το δεύτερο σημείο τομής πλησιάζει το σημείο της εφαπτομένης επ' αόριστον.
Αυτή η ιδιότητα λαμβάνεται ως ο ορισμός μιας εφαπτομένης όταν μιλάμε για οποιαδήποτε καμπύλη.

Έτσι, η εφαπτομένη στην καμπύλη ΑΒ (Εικ.) είναι η οριακή θέση ΜΤ προς την οποία τείνει η τέμνουσα ΜΝ όταν το σημείο τομής Ρ πλησιάζει το Μ χωρίς όριο.
Σημειώστε ότι η εφαπτομένη που ορίζεται με αυτόν τον τρόπο μπορεί να έχει περισσότερα από ένα κοινά σημεία με την καμπύλη (όπως φαίνεται στο Σχ.).
Ας θυμηθούμε τις περιπτώσεις της σχετικής θέσης μιας ευθείας και ενός κύκλου.
Δίνεται κύκλος με κέντρο O και ακτίνα r. Η ευθεία P, η απόσταση από το κέντρο προς την ευθεία, δηλαδή κάθετη στην ΟΜ, είναι ίση με d.
Περίπτωση 1- η απόσταση από το κέντρο του κύκλου στην ευθεία είναι μικρότερη από την ακτίνα του κύκλου:
Αποδείξαμε ότι στην περίπτωση που η απόσταση d είναι μικρότερη από την ακτίνα του κύκλου r, η ευθεία και ο κύκλος έχουν μόνο δύο κοινά σημεία (Εικ. 1).
Ρύζι. 1. Απεικόνιση για την περίπτωση 1
Περίπτωση δεύτερη- η απόσταση από το κέντρο του κύκλου στην ευθεία είναι ίση με την ακτίνα του κύκλου:
Έχουμε αποδείξει ότι σε αυτή την περίπτωση υπάρχει μόνο ένα κοινό σημείο (Εικ. 2).

Ρύζι. 2. Απεικόνιση για την περίπτωση 2
Περίπτωση 3- η απόσταση από το κέντρο του κύκλου στην ευθεία είναι μεγαλύτερη από την ακτίνα του κύκλου:
Αποδείξαμε ότι στην περίπτωση αυτή ο κύκλος και η ευθεία δεν έχουν κοινά σημεία (Εικ. 3).

Ρύζι. 3. Απεικόνιση για την περίπτωση 3
Σε αυτό το μάθημα μας ενδιαφέρει η δεύτερη περίπτωση, όταν μια ευθεία και ένας κύκλος έχουν ένα μόνο κοινό σημείο.
Ορισμός:
Μια ευθεία που έχει ένα μόνο κοινό σημείο με έναν κύκλο ονομάζεται εφαπτομένη στον κύκλο, ένα κοινό σημείο ονομάζεται εφαπτομένη της ευθείας και του κύκλου.
Η ευθεία p είναι μια εφαπτομένη, το σημείο Α είναι ένα σημείο εφαπτομένης (Εικ. 4).

Ρύζι. 4. Εφαπτομένη
Θεώρημα:
Η εφαπτομένη στον κύκλο είναι κάθετη στην ακτίνα που τραβιέται στο σημείο επαφής (Εικ. 5).

Ρύζι. 5. Απεικόνιση για το θεώρημα
Απόδειξη:
Αντίθετα, ας μην είναι η ΟΑ κάθετη στην ευθεία r. Σε αυτή την περίπτωση, χαμηλώνουμε μια κάθετη από το σημείο Ο στην ευθεία p, η οποία θα είναι η απόσταση από το κέντρο του κύκλου στην ευθεία:
Από ορθογώνιο τρίγωνο μπορούμε να πούμε ότι η υποτείνουσα ΟΗ είναι μικρότερη από το σκέλος ΟΑ, δηλαδή η ευθεία και ο κύκλος έχουν δύο κοινά σημεία, η ευθεία p είναι τέμνουσα. Έτσι, έχουμε μια αντίφαση, που σημαίνει ότι το θεώρημα είναι αποδεδειγμένο.

Ρύζι. 6. Απεικόνιση για το θεώρημα
Το θεώρημα της αντίστροφης είναι επίσης αληθές.
Θεώρημα:
Εάν μια ευθεία διέρχεται από το άκρο μιας ακτίνας που βρίσκεται σε έναν κύκλο και είναι κάθετη σε αυτήν την ακτίνα, τότε είναι εφαπτομένη.
Απόδειξη:
Εφόσον η ευθεία είναι κάθετη στην ακτίνα, η απόσταση ΟΑ είναι η απόσταση από την ευθεία μέχρι το κέντρο του κύκλου και είναι ίση με την ακτίνα: . Δηλαδή, και σε αυτή την περίπτωση, όπως αποδείξαμε προηγουμένως, η ευθεία και ο κύκλος έχουν το μόνο κοινό σημείο - το σημείο Α, επομένως η ευθεία p εφάπτεται στον κύκλο εξ ορισμού (Εικ. 7).

Ρύζι. 7. Απεικόνιση για το θεώρημα
Άμεση και αντίστροφο του θεωρήματοςμπορούν να συνδυαστούν ως εξής (Εικ. 8):
Δίνεται κύκλος με κέντρο Ο, ευθεία p, ακτίνα ΟΑ

Ρύζι. 8. Απεικόνιση για το θεώρημα
Θεώρημα:
Μια ευθεία γραμμή εφάπτεται σε έναν κύκλο εάν και μόνο αν η ακτίνα που σύρεται στο σημείο εφαπτομένης είναι κάθετη σε αυτόν.
Αυτό το θεώρημα σημαίνει ότι αν μια ευθεία είναι εφαπτομένη, τότε η ακτίνα που τραβιέται στο σημείο της εφαπτομένης είναι κάθετη σε αυτήν και αντίστροφα, από την καθετότητα της ΟΑ και της p προκύπτει ότι η p είναι εφαπτομένη, δηλαδή η ευθεία και ο κύκλος έχουν ένα κοινό σημείο.
Θεωρήστε δύο εφαπτομένες που σχεδιάζονται από ένα σημείο σε έναν κύκλο.
Θεώρημα:
Τα τμήματα των εφαπτομένων σε έναν κύκλο που σχεδιάζεται από ένα σημείο είναι ίσα και σχηματίζουν ίσες γωνίες με μια ευθεία γραμμή που τραβιέται μέσα από αυτό το σημείο και το κέντρο του κύκλου.
Δίνεται κύκλος, κέντρο Ο, σημείο Α έξω από τον κύκλο. Από το σημείο Α αντλούνται δύο εφαπτομένες, τα σημεία Β και Γ είναι σημεία εφαπτομένης. Πρέπει να αποδείξετε ότι οι γωνίες 3 και 4 είναι ίσες.

Ρύζι. 9. Απεικόνιση για το θεώρημα
Απόδειξη:
Η απόδειξη βασίζεται στην ισότητα των τριγώνων ![]() . Ας εξηγήσουμε την ισότητα των τριγώνων. Είναι ορθογώνια επειδή η ακτίνα που έλκεται στο σημείο επαφής είναι κάθετη στην εφαπτομένη. Αυτό σημαίνει ότι οι γωνίες είναι και ορθές και ίσες σε . Τα σκέλη OB και OS είναι ίσα, αφού είναι η ακτίνα του κύκλου. Η υποτείνουσα ΑΟ είναι γενική.
. Ας εξηγήσουμε την ισότητα των τριγώνων. Είναι ορθογώνια επειδή η ακτίνα που έλκεται στο σημείο επαφής είναι κάθετη στην εφαπτομένη. Αυτό σημαίνει ότι οι γωνίες είναι και ορθές και ίσες σε . Τα σκέλη OB και OS είναι ίσα, αφού είναι η ακτίνα του κύκλου. Η υποτείνουσα ΑΟ είναι γενική.
Έτσι, τα τρίγωνα είναι ίσα ως προς την ισότητα του σκέλους και της υποτείνουσας. Από εδώ είναι προφανές ότι τα σκέλη AB και AC είναι επίσης ίσα. Επίσης, οι γωνίες που βρίσκονται απέναντι από ίσες πλευρές είναι ίσες, πράγμα που σημαίνει ότι οι γωνίες και , είναι ίσες.
Το θεώρημα έχει αποδειχθεί.
Έτσι, εξοικειωθήκαμε με την έννοια της εφαπτομένης σε κύκλο, στο επόμενο μάθημα θα εξετάσουμε μέτρο βαθμούτόξα ενός κύκλου.
Βιβλιογραφία
- Alexandrov A.D. κλπ. Γεωμετρία 8η τάξη. - Μ.: Εκπαίδευση, 2006.
- Butuzov V.F., Kadomtsev S.B., Prasolov V.V. Γεωμετρία 8. - Μ.: Εκπαίδευση, 2011.
- Merzlyak A.G., Polonsky V.B., Yakir S.M. Γεωμετρία 8η τάξη. - Μ.: VENTANA-GRAF, 2009.
- Univer.omsk.su ().
- Oldskola1.narod.ru ().
- School6.aviel.ru ().
Εργασία για το σπίτι
- Atanasyan L.S., Butuzov V.F., Kadomtsev S.B. et al., Geometry 7-9, No. 634-637, p. 168.
Τέμνουσα, εφαπτομένη - όλα αυτά ακούγονταν εκατοντάδες φορές στα μαθήματα γεωμετρίας. Αλλά η αποφοίτηση από το σχολείο είναι πίσω μας, τα χρόνια περνούν και όλη αυτή η γνώση έχει ξεχαστεί. Τι πρέπει να θυμάστε;
Ουσία
Ο όρος «εφαπτομένη σε κύκλο» είναι πιθανώς γνωστός σε όλους. Αλλά είναι απίθανο όλοι να μπορέσουν να διατυπώσουν γρήγορα τον ορισμό του. Εν τω μεταξύ, μια εφαπτομένη είναι μια ευθεία γραμμή που βρίσκεται στο ίδιο επίπεδο με έναν κύκλο που την τέμνει μόνο σε ένα σημείο. Μπορεί να υπάρχει ένας τεράστιος αριθμός από αυτούς, αλλά όλοι έχουν ταυτόσημες ιδιότητες, το οποίο θα συζητηθεί παρακάτω. Όπως μπορείτε να μαντέψετε, το σημείο εφαπτομένης είναι το μέρος όπου τέμνονται ο κύκλος και η ευθεία. Σε κάθε συγκεκριμένη περίπτωση υπάρχει μόνο ένα, αλλά αν είναι περισσότερα από αυτά, τότε θα είναι ένα τμήμα.
Ιστορία ανακάλυψης και μελέτης
Η έννοια της εφαπτομένης εμφανίστηκε στην αρχαιότητα. Η κατασκευή αυτών των ευθειών γραμμών, πρώτα σε κύκλο, και στη συνέχεια σε ελλείψεις, παραβολές και υπερβολές χρησιμοποιώντας χάρακα και πυξίδα, πραγματοποιήθηκε ήδη από αρχικά στάδιαανάπτυξη της γεωμετρίας. Φυσικά, η ιστορία δεν έχει διατηρήσει το όνομα του ανακάλυψε, αλλά είναι προφανές ότι ακόμη και εκείνη την εποχή οι άνθρωποι ήταν αρκετά εξοικειωμένοι με τις ιδιότητες μιας εφαπτομένης σε έναν κύκλο.
Στη σύγχρονη εποχή, το ενδιαφέρον για αυτό το φαινόμενο φούντωσε ξανά - ένας νέος κύκλος μελέτης αυτής της έννοιας ξεκίνησε, σε συνδυασμό με την ανακάλυψη νέων καμπυλών. Έτσι, ο Γαλιλαίος εισήγαγε την έννοια του κυκλοειδούς και ο Φερμά και ο Ντεκάρτ κατασκεύασαν μια εφαπτομένη σε αυτό. Όσο για κύκλους, φαίνεται ότι δεν έχουν απομείνει μυστικά για τους αρχαίους σε αυτόν τον χώρο.
Ιδιότητες
Η ακτίνα που τραβιέται στο σημείο τομής θα είναι Αυτό
η κύρια, αλλά όχι η μόνη ιδιότητα που έχει μια εφαπτομένη σε κύκλο. Ένα άλλο σημαντικό χαρακτηριστικό περιλαμβάνει δύο ευθείες γραμμές. Έτσι, μέσω ενός σημείου που βρίσκεται έξω από τον κύκλο, μπορούν να σχεδιαστούν δύο εφαπτομένες και τα τμήματα τους θα είναι ίσα. Υπάρχει ένα άλλο θεώρημα για αυτό το θέμα, αλλά σπάνια εξετάζεται στο πλαίσιο του προτύπου σχολικό μάθημα, αν και είναι εξαιρετικά βολικό για την επίλυση ορισμένων προβλημάτων. Ακούγεται έτσι. Από ένα σημείο που βρίσκεται έξω από τον κύκλο, μια εφαπτομένη και μια τομή έλκονται σε αυτόν. Σχηματίζονται τα τμήματα AB, AC και AD. Το Α είναι η τομή των ευθειών, το Β είναι το σημείο εφαπτομένης, το C και το D είναι τομές. Στην περίπτωση αυτή θα ισχύει η ακόλουθη ισότητα: το μήκος της εφαπτομένης στον κύκλο, στο τετράγωνο, θα είναι ίσο με το γινόμενο των τμημάτων AC και AD.
Υπάρχει μια σημαντική συνέπεια από τα παραπάνω. Για κάθε σημείο του κύκλου μπορείτε να κατασκευάσετε μια εφαπτομένη, αλλά μόνο μία. Η απόδειξη αυτού είναι αρκετά απλή: θεωρητικά ρίχνοντας μια κάθετο από την ακτίνα πάνω της, διαπιστώνουμε ότι το σχηματισμένο τρίγωνο δεν μπορεί να υπάρξει. Και αυτό σημαίνει ότι η εφαπτομένη είναι η μόνη.
Κατασκευή
Μεταξύ άλλων προβλημάτων στη γεωμετρία υπάρχει μια ειδική κατηγορία, κατά κανόνα, όχι

αγαπήθηκε από μαθητές και φοιτητές. Για να λύσετε προβλήματα αυτής της κατηγορίας, χρειάζεστε μόνο μια πυξίδα και έναν χάρακα. Αυτές είναι εργασίες κατασκευής. Υπάρχουν επίσης για την κατασκευή μιας εφαπτομένης.
Έτσι, δίνεται ένας κύκλος και ένα σημείο που βρίσκεται έξω από τα όριά του. Και είναι απαραίτητο να σχεδιάσετε μια εφαπτομένη μέσα από αυτά. Πώς να το κάνετε αυτό; Πρώτα απ 'όλα, πρέπει να σχεδιάσετε ένα τμήμα μεταξύ του κέντρου του κύκλου O και δεδομένο σημείο. Στη συνέχεια χρησιμοποιήστε μια πυξίδα για να το χωρίσετε στη μέση. Για να το κάνετε αυτό, πρέπει να ορίσετε μια ακτίνα - λίγο περισσότερο από το μισό της απόστασης μεταξύ του κέντρου του αρχικού κύκλου και αυτού του σημείου. Μετά από αυτό, πρέπει να δημιουργήσετε δύο τεμνόμενα τόξα. Επιπλέον, η ακτίνα της πυξίδας δεν χρειάζεται να αλλάξει και το κέντρο κάθε τμήματος του κύκλου θα είναι το αρχικό σημείο και το Ο, αντίστοιχα. Οι διασταυρώσεις των τόξων πρέπει να συνδεθούν, γεγονός που θα χωρίσει το τμήμα στο μισό. Ορίστε μια ακτίνα στην πυξίδα ίση με αυτή την απόσταση. Στη συνέχεια, κατασκευάστε έναν άλλο κύκλο με το κέντρο στο σημείο τομής. Τόσο το αρχικό σημείο όσο και το O. Σε αυτήν την περίπτωση, θα υπάρχουν δύο ακόμη τομές με τον κύκλο που δίνεται στο πρόβλημα. Θα είναι τα σημεία επαφής για το αρχικά καθορισμένο σημείο.
Ήταν η κατασκευή των εφαπτομένων στον κύκλο που οδήγησε στη γέννηση

διαφορικός λογισμός. Το πρώτο έργο για αυτό το θέμα δημοσιεύτηκε από τον διάσημο Γερμανό μαθηματικό Leibniz. Προέβλεπε τη δυνατότητα εύρεσης μεγίστων, ελαχίστων και εφαπτομένων ανεξάρτητα από κλασματικά και παράλογα μεγέθη. Λοιπόν, τώρα χρησιμοποιείται για πολλούς άλλους υπολογισμούς.
Επιπλέον, η εφαπτομένη σε έναν κύκλο σχετίζεται με τη γεωμετρική έννοια της εφαπτομένης. Από εδώ προέρχεται το όνομά του. Μετάφραση από τα λατινικά tangens σημαίνει "εφαπτομένη". Έτσι, αυτή η έννοια συνδέεται όχι μόνο με τη γεωμετρία και τον διαφορικό λογισμό, αλλά και με την τριγωνομετρία.
Δύο κύκλοι
Η εφαπτομένη δεν επηρεάζει πάντα μόνο ένα σχήμα. Εάν ένας τεράστιος αριθμός ευθειών μπορεί να σχεδιαστεί σε έναν κύκλο, τότε γιατί όχι και το αντίστροφο; Μπορώ. Αλλά το έργο σε αυτή την περίπτωση γίνεται πολύ περίπλοκο, επειδή η εφαπτομένη σε δύο κύκλους μπορεί να μην περάσει από κανένα σημείο και η σχετική θέση όλων αυτών των σχημάτων μπορεί να είναι πολύ

διαφορετικός.
Τύποι και ποικιλίες
Όταν μιλάμε για δύο κύκλους και μία ή περισσότερες ευθείες, ακόμα κι αν είναι γνωστό ότι πρόκειται για εφαπτόμενες, δεν είναι αμέσως σαφές πώς βρίσκονται όλα αυτά τα σχήματα μεταξύ τους. Με βάση αυτό, διακρίνονται διάφορες ποικιλίες. Έτσι, οι κύκλοι μπορεί να έχουν ένα ή δύο κοινά σημεία ή να μην τα έχουν καθόλου. Στην πρώτη περίπτωση θα διασταυρωθούν και στη δεύτερη θα αγγίξουν. Και εδώ διακρίνονται δύο ποικιλίες. Εάν ένας κύκλος είναι ενσωματωμένος, όπως ήταν, στον δεύτερο, τότε η εφαπτομένη ονομάζεται εσωτερική, αν όχι, τότε εξωτερική. Μπορείτε να κατανοήσετε τη σχετική θέση των σχημάτων όχι μόνο με βάση το σχέδιο, αλλά και έχοντας πληροφορίες για το άθροισμα των ακτίνων τους και την απόσταση μεταξύ των κέντρων τους. Αν αυτές οι δύο ποσότητες είναι ίσες, τότε οι κύκλοι αγγίζουν. Αν το πρώτο είναι μεγαλύτερο τέμνονται και αν είναι μικρότερο τότε δεν έχουν κοινά σημεία.
Το ίδιο ισχύει και για τις ευθείες γραμμές. Για δύο κύκλους που δεν έχουν κοινά σημεία, μπορείτε

κατασκευάστε τέσσερις εφαπτόμενες. Δύο από αυτά θα τέμνονται μεταξύ των φιγούρων, ονομάζονται εσωτερικά. Κάποια άλλα είναι εξωτερικά.
Αν μιλάμε για κύκλους που έχουν ένα κοινό σημείο, τότε το πρόβλημα απλοποιείται πολύ. Το θέμα είναι ότι ό,τι και να γίνει σχετική θέσησε αυτή την περίπτωση θα έχουν μόνο μία εφαπτομένη. Και θα περάσει από το σημείο της τομής τους. Έτσι η κατασκευή δεν θα είναι δύσκολη.
Εάν τα σχήματα έχουν δύο σημεία τομής, τότε μπορεί να κατασκευαστεί μια ευθεία γραμμή για αυτά, εφαπτομένη στον κύκλο τόσο του ενός όσο και του άλλου, αλλά μόνο εξωτερική. Η λύση σε αυτό το πρόβλημα είναι παρόμοια με αυτή που θα συζητηθεί παρακάτω.
Επίλυση προβλήματος
Τόσο η εσωτερική όσο και η εξωτερική εφαπτομένη σε δύο κύκλους δεν είναι τόσο εύκολο να κατασκευαστούν, αν και αυτό το πρόβλημα μπορεί να λυθεί. Το γεγονός είναι ότι χρησιμοποιείται μια βοηθητική φιγούρα για αυτό, οπότε πρέπει να καταλήξετε σε αυτήν τη μέθοδο μόνοι σας

αρκετά προβληματική. Δίνονται λοιπόν δύο κύκλοι με διαφορετικές ακτίνες και κέντρα Ο1 και Ο2. Για αυτούς πρέπει να κατασκευάσετε δύο ζεύγη εφαπτομένων.
Πρώτα απ 'όλα, πρέπει να φτιάξετε ένα βοηθητικό κοντά στο κέντρο του μεγαλύτερου κύκλου. Σε αυτή την περίπτωση, η διαφορά μεταξύ των ακτίνων των δύο αρχικών σχημάτων θα πρέπει να καθοριστεί στην πυξίδα. Οι εφαπτομένες στον βοηθητικό κύκλο κατασκευάζονται από το κέντρο του μικρότερου κύκλου. Μετά από αυτό, σχεδιάζονται κάθετοι από το O1 και το O2 σε αυτές τις ευθείες μέχρι να τέμνονται με τα αρχικά σχήματα. Όπως προκύπτει από τη βασική ιδιότητα της εφαπτομένης, βρίσκονται τα απαιτούμενα σημεία και στους δύο κύκλους. Το πρόβλημα έχει λυθεί, τουλάχιστον το πρώτο μέρος.
Για να κατασκευάσετε εσωτερικές εφαπτομένες, θα πρέπει να λύσετε πρακτικά

παρόμοια εργασία. Και πάλι θα χρειαστείτε ένα βοηθητικό σχήμα, αλλά αυτή τη φορά η ακτίνα του θα είναι ίση με το άθροισμα των αρχικών. Οι εφαπτομένες κατασκευάζονται σε αυτό από το κέντρο ενός από αυτούς τους κύκλους. Η περαιτέρω πορεία της λύσης μπορεί να γίνει κατανοητή από το προηγούμενο παράδειγμα.
Η εφαπτομένη σε έναν κύκλο ή ακόμα και σε δύο ή περισσότερους δεν είναι τόσο δύσκολο έργο. Φυσικά, οι μαθηματικοί έχουν σταματήσει εδώ και καιρό να λύνουν τέτοια προβλήματα χειροκίνητα και βασίζονται σε υπολογισμούς ειδικά προγράμματα. Αλλά δεν πρέπει να νομίζετε ότι τώρα δεν χρειάζεται να μπορείτε να το κάνετε μόνοι σας, γιατί για να διατυπώσετε σωστά μια εργασία για έναν υπολογιστή πρέπει να κάνετε και να καταλάβετε πολλά. Δυστυχώς, υπάρχουν ανησυχίες ότι μετά την τελική μετάβαση σε μια δοκιμαστική μορφή ελέγχου γνώσης, οι εργασίες κατασκευής θα προκαλούν ολοένα και περισσότερες δυσκολίες στους μαθητές.
Όσον αφορά την εύρεση κοινών εφαπτομένων για μεγαλύτερο αριθμό κύκλων, αυτό δεν είναι πάντα δυνατό, ακόμα κι αν βρίσκονται στο ίδιο επίπεδο. Αλλά σε ορισμένες περιπτώσεις μπορείτε να βρείτε μια τέτοια ευθεία γραμμή.
Παραδείγματα από τη ζωή
Μια κοινή εφαπτομένη σε δύο κύκλους εμφανίζεται συχνά στην πράξη, αν και αυτό δεν είναι πάντα αισθητό. Μεταφορείς, συστήματα μπλοκ, ιμάντες μετάδοσης τροχαλίας, τάνυση νήματος σε μια ραπτομηχανή, ακόμα και απλώς μια αλυσίδα ποδηλάτου - όλα αυτά είναι πραγματικά παραδείγματα. Επομένως, δεν πρέπει να πιστεύετε ότι τα γεωμετρικά προβλήματα παραμένουν μόνο στη θεωρία: στη μηχανική, τη φυσική, τις κατασκευές και πολλούς άλλους τομείς βρίσκουν πρακτική εφαρμογή.
Τις περισσότερες φορές, είναι γεωμετρικά προβλήματα που προκαλούν δυσκολίες στους υποψήφιους, τους αποφοίτους και τους συμμετέχοντες μαθηματικές ολυμπιάδες. Αν κοιτάξετε τα στατιστικά στοιχεία του Unified State Exam 2010, μπορείτε να το δείτε γεωμετρικό πρόβλημαΠερίπου το 12% των συμμετεχόντων ξεκίνησαν το C4, αλλά μόνο το 0,2% των συμμετεχόντων έλαβε πλήρη βαθμολογία και συνολικά η εργασία αποδείχθηκε η πιο δύσκολη από όλες αυτές που προτάθηκαν.
Προφανώς, όσο πιο γρήγορα προσφέρουμε στους μαθητές όμορφους ή απροσδόκητους τρόπους επίλυσης προβλημάτων, τόσο μεγαλύτερη είναι η πιθανότητα να τους κάνουμε να ενδιαφερθούν και να αιχμαλωτιστούν σοβαρά και για μεγάλο χρονικό διάστημα. Μα πόσο δύσκολο είναι να βρεις ενδιαφέρον και σύνθετες εργασίεςστο επίπεδο της 7ης τάξης, όταν μόλις αρχίζει η συστηματική μελέτη της γεωμετρίας. Τι μπορεί να προσφερθεί σε έναν μαθητή που ενδιαφέρεται για τα μαθηματικά που γνωρίζει μόνο τα σημάδια ισότητας των τριγώνων και τις ιδιότητες γειτονικών και κάθετων γωνιών; Ωστόσο, μπορεί κανείς να εισαγάγει την έννοια της εφαπτομένης σε έναν κύκλο, ως ευθεία γραμμή που έχει ένα κοινό σημείο με τον κύκλο. Ας υποθέσουμε ότι η ακτίνα που τραβιέται στο σημείο επαφής είναι κάθετη στην εφαπτομένη. Αξίζει βέβαια να εξεταστούν όλες οι πιθανές περιπτώσεις διάταξης δύο κύκλων και κοινών εφαπτομένων σε αυτούς, οι οποίες μπορούν να σχεδιαστούν από το μηδέν έως το τέσσερα. Αποδεικνύοντας τα θεωρήματα που προτείνονται παρακάτω, μπορείτε να επεκτείνετε σημαντικά το σύνολο προβλημάτων για τους μαθητές της έβδομης δημοτικού. Ταυτόχρονα, αποδεικνύονται ταυτόχρονα σημαντικά ή απλά ενδιαφέροντα και ΑΣΤΕΙΑ ΓΕΓΟΝΟΤΑ. Επιπλέον, δεδομένου ότι πολλές δηλώσεις δεν περιλαμβάνονται στο σχολικό εγχειρίδιο, μπορούν να συζητηθούν σε κυκλικές τάξεις και με τους αποφοίτους κατά την επανάληψη της επιπεδομετρίας. Αυτά τα γεγονότα αποδείχθηκαν σχετικά την περασμένη ακαδημαϊκή χρονιά. Δεδομένου ότι πολλές διαγνωστικές εργασίες καθαυτές Εργασία Ενιαίας Κρατικής Εξεταστικήςπεριείχε ένα πρόβλημα για τη λύση του οποίου ήταν απαραίτητο να χρησιμοποιηθεί η ιδιότητα του εφαπτομενικού τμήματος που αποδεικνύεται παρακάτω.
Τ 1
Τμήματα εφαπτομένων σε κύκλο που σχεδιάζονται από
ίσο με ένα σημείο (Εικ. 1)
Αυτό είναι το θεώρημα που μπορείτε να εισαγάγετε πρώτα στους μαθητές της έβδομης δημοτικού.
Στη διαδικασία της απόδειξης χρησιμοποιήσαμε το πρόσημο της ισότητας των ορθογωνίων τριγώνων και καταλήξαμε στο συμπέρασμα ότι το κέντρο του κύκλου βρίσκεται στη διχοτόμο της γωνίας BSA.
Στην πορεία, θυμηθήκαμε ότι η διχοτόμος μιας γωνίας είναι ο τόπος των σημείων στην εσωτερική περιοχή της γωνίας, σε ίση απόσταση από τις πλευρές της. Η λύση σε ένα κάθε άλλο παρά τετριμμένο πρόβλημα βασίζεται σε αυτά τα δεδομένα, προσβάσιμα ακόμη και σε εκείνους που μόλις αρχίζουν να μελετούν τη γεωμετρία.

1. Διχοτόμοι γωνίας ΕΝΑ, ΣΕΚαι ΜΕκυρτό τετράπλευρο Α Β Γ Δτέμνονται σε ένα σημείο. Ακτίνες ΑΒΚαι DCτέμνονται σε ένα σημείο μικαι οι ακτίνες
ΉλιοςΚαι ΕΝΑ Δστο σημείο φά. Να αποδείξετε ότι ένα μη κυρτό τετράπλευρο AECFτα αθροίσματα των μηκών των απέναντι πλευρών είναι ίσα.
Λύση (Εικ. 2).Αφήνω ΣΧΕΤΙΚΑ ΜΕ– σημείο τομής αυτών των διχοτόμων. Επειτα ΣΧΕΤΙΚΑ ΜΕίση απόσταση από όλες τις πλευρές του τετράπλευρου Α Β Γ Δ, αυτό είναι
είναι το κέντρο ενός κύκλου εγγεγραμμένου σε τετράπλευρο. Με θεώρημα 1
ισχύουν οι ακόλουθες ισότητες: AR = Ο Α.Κ.,
ER = Ε.Π., F.T. = FK. Ας προσθέσουμε την αριστερή και τη δεξιά πλευρά ανά όρο και πάρουμε τη σωστή ισότητα:
(AR + ER) + F.T. = (Ο Α.Κ. +FK) + Ε.Π.; Η A.E. + (F.C. + C.T.) = Ο Α.Φ. + (ΕΕ + Η/Υ). Επειδή ST = RS, Οτι ΑΕ + F.C. = Ο Α.Φ. + ΕΕ, που ήταν αυτό που έπρεπε να αποδειχθεί.
Ας εξετάσουμε ένα πρόβλημα με μια ασυνήθιστη διατύπωση, για τη λύση του οποίου αρκεί να γνωρίζουμε το θεώρημα 1 .
2. Υπάρχει n- τρίγωνο του οποίου οι πλευρές είναι διαδοχικά 1, 2, 3, ..., n, στον οποίο μπορεί να εγγραφεί ένας κύκλος;
Λύση. Ας το πούμε αυτό n-Γον υπάρχει. ΕΝΑ 1 ΕΝΑ 2 =1, …, ΕΝΑ n-1 ΕΝΑ n= n– 1,ΕΝΑ n ΕΝΑ 1 = n. σι 1 , …, σι n – αντίστοιχα σημεία επαφής. Στη συνέχεια από το Θεώρημα 1 ΕΝΑ 1 σι 1 = ΕΝΑ 1 σι n< 1, n – 1 < ΕΝΑ n σι n< n.Με την ιδιότητα των εφαπτομένων τμημάτων ΕΝΑ n σι n= ΕΝΑ n σι n-1. Αλλά, ΕΝΑ n σι n-1< ΕΝΑ n-1 ΕΝΑ n= n - 1. Αντίφαση. Επομένως όχι n-η ικανοποίηση των συνθηκών του προβλήματος.

Τ 2Τα αθροίσματα των απέναντι πλευρών ενός τετράπλευρου που περιγράφονται περίπου
οι κύκλοι είναι ίσοι (Εικ. 3)
Οι μαθητές, κατά κανόνα, αποδεικνύουν εύκολα αυτήν την ιδιότητα του περιγραφόμενου τετράπλευρου. Αφού αποδείξουμε το θεώρημα 1 , είναι μια προπονητική άσκηση. Μπορούμε να γενικεύσουμε αυτό το γεγονός - τα αθροίσματα των πλευρών ενός περιγεγραμμένου ζυγού τριγώνου, που λαμβάνονται από τη μία πλευρά, είναι ίσα. Για παράδειγμα, για ένα εξάγωνο ABCDEFσωστά: AB + CD + EF = BC + DE + FA.

Λύση (Εικ. 1). Εφόσον τα τετράπλευρα ABEF και ECDF είναι κυκλικά, τότε από το Θεώρημα 2 P ABEF = 2(AB + EF) και P ECDF = 2 (CD + EF), κατά συνθήκη
P ABEF – P ECDF = 2(AB + EF) – 2(CD + EF) = 2p. AB – CD = p. AB = a + p.

σχεδιάζεται μια εφαπτομένη στον κύκλο που τέμνει τα τμήματα ΑΒΚαι ΜΕΤΑ ΧΡΙΣΤΟΝσε σημεία ΜΚαι Rαντίστοιχα. Να αποδείξετε ότι η περίμετρος ενός τριγώνου AMRκαι το μέγεθος της γωνίας MPAδεν εξαρτώνται από την επιλογή του σημείου Χ.
Λύση (Εικ. 5).Με το Θεώρημα 1 MV = MX και RS = RH.Επομένως, η περίμετρος του τριγώνου AMRίσο με το άθροισμα των τμημάτων ΑΒΚαι ΜΕΤΑ ΧΡΙΣΤΟΝ.Ή διπλή εφαπτομένη που σύρεται στον κύκλο για ένα τρίγωνο AMR . Η τιμή της γωνίας MOP μετριέται κατά το ήμισυ της γωνίας VOS, το οποίο δεν εξαρτάται από την επιλογή του σημείου Χ.

Λύση (Εικ. 6). Μέθοδος πρώτη (αλγεβρική). Αφήνω ΑΚ = ΑΝ = x,Επειτα BK = BM = c – x, CM = CN = a – c + x. AC = AN + NC,τότε μπορούμε να δημιουργήσουμε μια εξίσωση για x: b = x + (a – c + x).Οπου
![]() .
.
Μέθοδος δεύτερη (γεωμετρική). Ας δούμε το διάγραμμα. Τμήματα ίσων εφαπτομένων, που λαμβάνονται ένα κάθε φορά, αθροίζονται στην ημιπερίμετρο
τρίγωνο. Το κόκκινο και το πράσινο συνθέτουν μια πλευρά ΕΝΑ.Στη συνέχεια το τμήμα που μας ενδιαφέρει x = p – a.Φυσικά, τα αποτελέσματα που προέκυψαν συμπίπτουν.


4. Βρείτε την ακτίνα ενός κύκλου εγγεγραμμένου σε ορθογώνιο τρίγωνο με σκέλη α, βκαι υποτείνουσα Με. Λύση (Εικ. 8). Τεντάξει πως OMCN -τετράγωνο, τότε η ακτίνα του εγγεγραμμένου κύκλου είναι ίση με το εφαπτομενικό τμήμα CN.
![]() .
.


5. Να αποδείξετε ότι τα σημεία εφαπτομένης του εγγεγραμμένου και του κύκλου με την πλευρά του τριγώνου είναι συμμετρικά ως προς το μέσον αυτής της πλευράς.
Λύση (Εικ. 9).Σημειώστε ότι το AK είναι ένα εφαπτόμενο τμήμα του κύκλου για ένα τρίγωνο ΑΛΦΑΒΗΤΟ.Σύμφωνα με τον τύπο (2)
![]() . VM- ευθύγραμμο τμήμα
εφαπτομένη στον κύκλο για ένα τρίγωνο ΑΛΦΑΒΗΤΟ.Σύμφωνα με τον τύπο (1)
. VM- ευθύγραμμο τμήμα
εφαπτομένη στον κύκλο για ένα τρίγωνο ΑΛΦΑΒΗΤΟ.Σύμφωνα με τον τύπο (1)
![]() . AK = VM,και αυτό σημαίνει ότι τα σημεία Κ και Μίση απόσταση από τη μέση της πλευράς AB, Q.E.D.
. AK = VM,και αυτό σημαίνει ότι τα σημεία Κ και Μίση απόσταση από τη μέση της πλευράς AB, Q.E.D.

6. Δύο κοινές εξωτερικές εφαπτομένες και μία εσωτερική εφαπτομένη σχεδιάζονται σε δύο κύκλους. Η εσωτερική εφαπτομένη τέμνει τις εξωτερικές εφαπτομένες σε σημεία Α, Βκαι αγγίζει τους κύκλους σε σημεία Α'1Και ΣΕ 1 .Αποδείξτε το AA 1 = BB 1.
Λύση (Εικ. 10). Σταμάτα... Τι να αποφασίσεις; Αυτή είναι απλώς μια διαφορετική διατύπωση του προηγούμενου προβλήματος. Προφανώς, ένας από τους κύκλους είναι εγγεγραμμένος και ο άλλος είναι κύκλος για ένα συγκεκριμένο τρίγωνο ΑΛΦΑΒΗΤΟ.Και τα τμήματα AA 1 και BB 1αντιστοιχούν σε τμήματα ΑΚΚαι VMεργασίες 5. Αξίζει να σημειωθεί ότι το έργο που προτείνεται στις Πανρωσική Ολυμπιάδαμαθητών στα μαθηματικά, λύνεται με τόσο προφανή τρόπο.

7. Οι πλευρές του πενταγώνου με τη σειρά διέλευσης είναι 5, 6, 10, 7, 8. Αποδείξτε ότι δεν μπορεί να εγγραφεί κύκλος σε αυτό το πεντάγωνο.
Λύση (Εικ. 11). Ας υποθέσουμε ότι σε ένα πεντάγωνο ABCDEμπορείτε να εγγράψετε έναν κύκλο. Επιπλέον, τα κόμματα ΑΒ, ΠΡΟ ΧΡΙΣΤΟΥ., CD, DEΚαι EAείναι ίσα με 5, 6, 10, 7 και 8, αντίστοιχα. Ας σημειώσουμε τα εφαπτομενικά σημεία με τη σειρά – φά, σολ, H, ΜΚαι Ν. Αφήστε το μήκος του τμήματος Ο Α.Φ.ίσο με Χ.
Επειτα B.F. = FD – Ο Α.Φ. = 5 – Χ = B.G.. G.C. = ΠΡΟ ΧΡΙΣΤΟΥ. – B.G. = = 6 – (5 – Χ) = 1 + Χ = CH. Και ούτω καθεξής: HD = DM = 9 – Χ; ΜΟΥ. = EN = Χ – 2, ΕΝΑ = 10 – Χ.
Αλλά, Ο Α.Φ. = ΕΝΑ. δηλαδή 10 - Χ = Χ; Χ= 5. Ωστόσο, το εφαπτομενικό τμήμα Ο Α.Φ.δεν μπορεί να είναι ίση πλευρά ΑΒ. Η αντίφαση που προκύπτει αποδεικνύει ότι ένας κύκλος δεν μπορεί να εγγραφεί σε ένα δεδομένο πεντάγωνο.
8. Ένας κύκλος είναι εγγεγραμμένος σε ένα εξάγωνο· οι πλευρές του με τη σειρά της περιφοράς είναι 1, 2, 3, 4, 5. Βρείτε το μήκος της έκτης πλευράς.
Λύση. Φυσικά, μπορούμε να ορίσουμε ένα εφαπτόμενο τμήμα ως Χ, όπως και στο προηγούμενο πρόβλημα, δημιουργήστε μια εξίσωση και λάβετε την απάντηση. Όμως, είναι πολύ πιο αποτελεσματικό και αποτελεσματικό να χρησιμοποιούμε μια σημείωση στο θεώρημα 2 : τα αθροίσματα των πλευρών ενός περιγεγραμμένου εξαγώνου, που λαμβάνονται το ένα μέσα από το άλλο, είναι ίσα.
Τότε 1 + 3 + 5 = 2 + 4 + Χ, Οπου Χ– άγνωστη έκτη πλευρά, Χ = 3.

Λύση (Εικ. 12). Δεδομένου ότι τα μήκη όλων των πλευρών είναι ακέραιοι, τα κλασματικά μέρη των μηκών των τμημάτων είναι ίσα BT, B.P., DM, DN, Ο Α.Κ.Και ΣΤΟ. Εχουμε ΣΤΟ + τηλεόραση= 1, και κλασματικά μέρη μηκών τμήματος ΣΤΟΚαι ΤΒείναι ίσα. Αυτό είναι δυνατό μόνο όταν ΣΤΟ + τηλεόραση= 0,5. Με θεώρημα 1
VT + VR.
Που σημαίνει, VR= 0,5. Σημειώστε ότι η συνθήκη CD= 3 αποδείχθηκαν αζήτητα. Προφανώς, οι συντάκτες του προβλήματος υπέθεσαν κάποια άλλη λύση. Απάντηση: 0,5.

10. Σε τετράγωνο ABCD AD = DC, AB = 3, BC = 5.Κύκλοι εγγεγραμμένοι σε τρίγωνα ABDΚαι CBDαγγίξτε ένα τμήμα BDσε σημεία ΜΚαι Ναντίστοιχα. Βρείτε το μήκος του τμήματος MN.
Λύση (Εικ. 13). MN = DN – DM.Σύμφωνα με τον τύπο (1) για τρίγωνα DBAΚαι DBCαναλόγως έχουμε:

11. Σε τετράγωνο Α Β Γ Δμπορείτε να εγγράψετε έναν κύκλο. Κύκλοι εγγεγραμμένοι σε τρίγωνα ABDΚαι CBDέχουν ακτίνες RΚαι rαντίστοιχα. Βρείτε την απόσταση μεταξύ των κέντρων αυτών των κύκλων.
Λύση (Εικ. 13). Αφού κατά συνθήκη το τετράπλευρο Α Β Γ Δεγγεγραμμένο, από θεώρημα 2 έχουμε: AB + DC = AD + BC.Ας χρησιμοποιήσουμε την ιδέα της επίλυσης του προηγούμενου προβλήματος. . Αυτό σημαίνει ότι τα σημεία επαφής των κύκλων με το τμήμα DMταιριάξει. Η απόσταση μεταξύ των κέντρων των κύκλων είναι ίση με το άθροισμα των ακτίνων. Απάντηση: R+r.
Μάλιστα, έχει αποδειχθεί ότι η συνθήκη είναι σε τετράπλευρο Α Β Γ Δμπορείτε να εγγράψετε έναν κύκλο, ισοδύναμο με την συνθήκη - in κυρτό τετράπλευρο Α Β Γ Δκύκλοι εγγεγραμμένοι σε τρίγωνα αλφάβητοΚαι ADCαγγίζουν ο ένας τον άλλον. Το αντίθετο ισχύει.
Προτείνεται να αποδειχθούν αυτές οι δύο αμοιβαία αντίστροφες προτάσεις στο παρακάτω πρόβλημα, το οποίο μπορεί να θεωρηθεί ως γενίκευση αυτού του προβλήματος.

12. Σε κυρτό τετράπλευρο Α Β Γ Δ (ρύζι. 14) κύκλοι εγγεγραμμένοι σε τρίγωνα αλφάβητοΚαι ADCαγγίζουν ο ένας τον άλλον. Αποδείξτε ότι κύκλοι εγγεγραμμένοι σε τρίγωνα ABDΚαι BDCαγγίζουν επίσης ο ένας τον άλλον.

13. Σε τρίγωνο αλφάβητομε τα κόμματα α, βΚαι ντοστην άκρη Ήλιοςσημειωμένο σημείο ρεέτσι ώστε κύκλοι εγγεγραμμένοι σε τρίγωνα ABDΚαι ACDαγγίξτε ένα τμήμα ΕΝΑ Δσε ένα σημείο. Βρείτε το μήκος του τμήματος BD.
Λύση (Εικ. 15). Ας εφαρμόσουμε τον τύπο (1) για τρίγωνα ADCΚαι A.D.B., υπολογισμός DMδύο 
Καταλήγει, ρε– σημείο επαφής με το πλάι Ήλιοςκύκλος εγγεγραμμένος σε τρίγωνο αλφάβητο. Το αντίθετο ισχύει: αν η κορυφή ενός τριγώνου συνδέεται με το σημείο εφαπτομένης ενός εγγεγραμμένου κύκλου στην αντίθετη πλευρά, τότε οι κύκλοι που εγγράφονται στα τρίγωνα που προκύπτουν ακουμπούν ο ένας τον άλλον.

14. Κέντρα ΣΧΕΤΙΚΑ ΜΕ 1 , ΣΧΕΤΙΚΑ ΜΕ 2 και ΣΧΕΤΙΚΑ ΜΕ 3 τρεις μη τεμνόμενοι κύκλοι της ίδιας ακτίνας βρίσκονται στις κορυφές ενός τριγώνου. Από σημεία ΣΧΕΤΙΚΑ ΜΕ 1 , ΣΧΕΤΙΚΑ ΜΕ 2 , ΣΧΕΤΙΚΑ ΜΕ 3, οι εφαπτομένες σε αυτούς τους κύκλους σχεδιάζονται όπως φαίνεται στο σχήμα.
Είναι γνωστό ότι αυτές οι εφαπτομένες, τέμνουσες, σχημάτισαν ένα κυρτό εξάγωνο, οι πλευρές του οποίου είναι βαμμένες με κόκκινο και μπλε. Να αποδείξετε ότι το άθροισμα των μηκών των κόκκινων τμημάτων είναι ίσο με το άθροισμα των μηκών των μπλε.
Λύση (Εικ. 16). Είναι σημαντικό να κατανοήσουμε πώς να χρησιμοποιήσετε το γεγονός ότι οι δεδομένοι κύκλοι έχουν ίσες ακτίνες. Σημειώστε ότι τα τμήματα BRΚαι DMείναι ίσα, που προκύπτει από την ισότητα των ορθογωνίων τριγώνων ΣΧΕΤΙΚΑ ΜΕ 1 BRΚαι Ο 2 Β.Μ.. Επίσης D.L. = Δ.Π., FN = FK. Προσθέτουμε τις ισότητες ανά όρο και μετά αφαιρούμε από τα προκύπτοντα αθροίσματα πανομοιότυπα τμήματα εφαπτομένων που προέρχονται από τις κορυφές ΕΝΑ, ΜΕ, Και μιεξάγωνο ABCDEF: ARΚαι Ο Α.Κ., C.L.Και ΕΚ., ENΚαι Ε.Π.. Παίρνουμε αυτό που χρειαζόμαστε.
Εδώ είναι ένα παράδειγμα ενός προβλήματος στη στερεομετρία, που προτάθηκε στο XII Διεθνές Μαθηματικό Τουρνουά για μαθητές Λυκείου "Κύπελλο στη μνήμη του A. N. Kolmogorov".
16. Δίνεται μια πενταγωνική πυραμίδα SA 1 A 2 A 3 A 4 A 5 .Υπάρχει μια σφαίρα w,που αγγίζει όλες τις άκρες της πυραμίδας και μια άλλη σφαίρα w 1,που αγγίζει όλες τις πλευρές της βάσης Α 1 Α 2 Α 3 Α 4 Α 5και συνέχειες των πλευρικών πλευρών SA 1, SA 2, SA 3, SA 4, SA 5πέρα από τις κορυφές της βάσης. Να αποδείξετε ότι η κορυφή της πυραμίδας έχει ίση απόσταση από τις κορυφές της βάσης. (Berlov S. L., Karpov D. V.)

αφού τα εφαπτόμενα τμήματα είναι ίσα. Αφήνω C i A i = a i. Επειτα p SAiAi +1 = s+a i +a i+1, και από την ισότητα των περιμέτρων προκύπτει ότι ένα 1 = ένα 3 = ένα 5 = ένα 2 = ένα 4, από όπου ΑΝΩΝΥΜΗ ΕΤΑΙΡΙΑ. 1 = ΑΝΩΝΥΜΗ ΕΤΑΙΡΙΑ. 2 = ΑΝΩΝΥΜΗ ΕΤΑΙΡΙΑ. 3 = ΑΝΩΝΥΜΗ ΕΤΑΙΡΙΑ. 4 = ΑΝΩΝΥΜΗ ΕΤΑΙΡΙΑ. 5 .
17. Ενιαία Κρατική Εξέταση. Διαγνωστική εργασία 8.12.2009, S–4.Δίνεται τραπεζοειδές Α Β Γ Δ, τα θεμέλια του οποίου π.Χ. = 44,ΕΝΑ Δ = 100, ΑΒ = CD= 35. Κύκλος εφαπτόμενος σε ευθείες ΕΝΑ ΔΚαι ΜΕΤΑ ΧΡΙΣΤΟΝ., αγγίζει το πλάι CDστο σημείο κ. Βρείτε το μήκος του τμήματος CK.BDC και BDA, αγγίξτε τα πλαϊνά ВDσε σημεία μιΚαι φά. Βρείτε το μήκος του τμήματος Η Ε.Φ..
Λύση. Δύο περιπτώσεις είναι δυνατές (Εικ. 20 και Εικ. 21). Χρησιμοποιώντας τον τύπο (1) βρίσκουμε τα μήκη των τμημάτων DEΚαι DF.

Στην πρώτη περίπτωση ΕΝΑ Δ = 0,1ΜΕΤΑ ΧΡΙΣΤΟΝ, CD = 0,9ΜΕΤΑ ΧΡΙΣΤΟΝ.. Στο δεύτερο - ΕΝΑ Δ = 0,125ΜΕΤΑ ΧΡΙΣΤΟΝ, CD = 1,125ΜΕΤΑ ΧΡΙΣΤΟΝ.. Αντικαθιστούμε τα δεδομένα και παίρνουμε την απάντηση: 4.6 ή 5.5.
Προβλήματα για ανεξάρτητη λύση/

1. Η περίμετρος ενός ισοσκελούς τραπεζοειδούς περιγεγραμμένου σε κύκλο είναι ίση με 2 τρίψτε.Βρείτε την προβολή της διαγωνίου του τραπεζοειδούς στη μεγαλύτερη βάση. (1/2r)
2. Ανοιχτή τράπεζα Προβλήματα Ενιαίας Κρατικής Εξέτασηςμαθηματικά. ΣΤΙΣ 4. Σε κύκλο εγγεγραμμένο σε τρίγωνο ABC (Εικ. 22),σχεδιάζονται τρεις εφαπτομένες. Οι περίμετροι των κομμένων τριγώνων είναι 6, 8, 10. Βρείτε την περίμετρο αυτού του τριγώνου. (24)
3. Σε τρίγωνο αλφάβητοκύκλος είναι εγγεγραμμένος. MN -εφαπτομένη στον κύκλο, MÎ AC, NÎ BC, BC = 13, AC = 14, AB = 15.Να βρείτε την περίμετρο του τριγώνου MNC. (12)
4. Σε κύκλο εγγεγραμμένο σε τετράγωνο με πλευρά α, σχεδιάζεται μια εφαπτομένη που τέμνει τις δύο πλευρές του. Βρείτε την περίμετρο του κομμένου τριγώνου. (ΕΝΑ)
5. Ένας κύκλος εγγράφεται σε πεντάγωνο με πλευρές ΕΝΑ, ρε, ντο, ρεΚαι μι. Βρείτε τα τμήματα στα οποία το σημείο εφαπτομένης χωρίζει την πλευρά ίση με ΕΝΑ.
6. Ένας κύκλος εγγράφεται σε ένα τρίγωνο με πλευρές 6, 10 και 12. Τραβιέται μια εφαπτομένη στον κύκλο έτσι ώστε να τέμνει δύο μεγάλες πλευρές. Βρείτε την περίμετρο του κομμένου τριγώνου. (16)
7. CD– διάμεσος του τριγώνου αλφάβητο. Κύκλοι εγγεγραμμένοι σε τρίγωνα ACDΚαι BCD, αγγίξτε το τμήμα CDσε σημεία ΜΚαι Ν. Εύρημα MN, Αν ΜΕΤΑ ΧΡΙΣΤΟΝ – Ήλιος = 2. (1)
8. Σε τρίγωνο αλφάβητομε τα κόμματα α, βΚαι ντοστην άκρη Ήλιοςσημειωμένο σημείο ρε. Σε κύκλους εγγεγραμμένους σε τρίγωνα ABDΚαι ACD, μια κοινή εφαπτομένη σχεδιάζεται τέμνουσα ΕΝΑ Δστο σημείο Μ. Βρείτε το μήκος του τμήματος ΕΙΜΑΙ. (Μήκος ΕΙΜΑΙδεν εξαρτάται από τη θέση του σημείου ρεΚαι
ίσο με ½ ( γ + β – α))
9. Β ορθογώνιο τρίγωνοεγγεγραμμένο σε κύκλο ακτίνας ΕΝΑ. Η ακτίνα του κύκλου που εφάπτεται στην υποτείνουσα και τις προεκτάσεις των ποδιών είναι ίση με R.Να βρείτε το μήκος της υποτείνουσας. ( R–a)
10. Σε τρίγωνο αλφάβητοτα μήκη των πλευρών είναι γνωστά: ΑΒ = Με, ΜΕΤΑ ΧΡΙΣΤΟΝ = σι, Ήλιος = ΕΝΑ. Ένας κύκλος εγγεγραμμένος σε τρίγωνο αγγίζει μια πλευρά ΑΒστο σημείο Γ 1. Ο κύκλος αγγίζει την προέκταση της πλευράς ΑΒανά πόντο ΕΝΑστο σημείο Γ 2. Προσδιορίστε το μήκος του τμήματος C 1 C 2. (σι)
11. Βρείτε τα μήκη των πλευρών του τριγώνου διαιρεμένα με το σημείο εφαπτομένης του εγγεγραμμένου κύκλου ακτίνας 3 cm σε τμήματα 4 cm και 3 cm (7, 24 και 25 cm σε ορθογώνιο τρίγωνο)
12. Ολυμπιάδα Soros 1996, 2ος γύρος, 11η τάξη. Δίνεται ένα τρίγωνο αλφάβητο, στις πλευρές των οποίων σημειώνονται σημεία Α 1, Β 1, Γ 1. Ακτίνες κύκλων εγγεγραμμένων σε τρίγωνα AC 1 B 1, BC 1 A 1, SA 1 B 1ίσο σε r. Ακτίνα κύκλου εγγεγραμμένου σε τρίγωνο Α 1 Β 1 Γ 1ισοδυναμεί R. Βρείτε την ακτίνα ενός κύκλου εγγεγραμμένου σε τρίγωνο αλφάβητο. (R +r).
Τα προβλήματα 4–8 προέρχονται από το βιβλίο προβλημάτων του Gordin R.K. «Geometry. Πλανομετρία." Μόσχα. Εκδοτικός οίκος MCNMO. 2004.